We included HMH Into Math Grade 5 Answer Key PDF Module 6 Lesson 3 Represent Subtraction with Different-Sized Parts to make students experts in learning maths.
HMH Into Math Grade 5 Module 6 Lesson 3 Answer Key Represent Subtraction with Different-Sized Parts
I Can represent the difference between fractions with different-sized parts using a visual model.
Spark Your Learning
Mark and his friends are putting on a play. Mark is in charge of the costumes. He measures each sleeve in one costume to be \(\frac{3}{4}\) yard long. Each sleeve should be \(\frac{1}{2}\) yard long. By how much should each sleeve be shortened?

Draw a visual model to represent how much each sleeve should be shortened.

By how much should each sleeve be shortened? ______
Answer:
Given,
Mark and his friends are putting on a play. Mark is in charge of the costumes.
He measures each sleeve in one costume to be \(\frac{3}{4}\) yard long.
Each sleeve should be \(\frac{1}{2}\) yard long.
\(\frac{3}{4}\) – \(\frac{1}{2}\)
LCD is 4.
\(\frac{3}{4}\) – \(\frac{2}{4}\) = \(\frac{1}{4}\) yard
Turn and Talk What part of the visual model shows how much each sleeve should be shortened? How do you know?
Build Understanding
1. Anderson and Joanne sold tickets for the play. Anderson sold \(\frac{3}{4}\) of the roll of tickets, and Joanne sold \(\frac{1}{6}\) of the roll of tickets.

What is the difference between the fractions of the roll of tickets that Anderson and Joanne sold?
A. Explain what the dashed box in the fraction model represents.
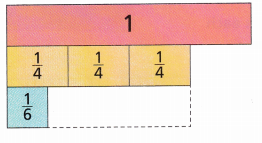
B. Who sold more tickets? How do you know?
C. Use the fraction model in Part A to draw fraction strips in the dashed box to solve the problem. What size fraction strips did you draw? Explain.
D. What is the difference between the fractions of the roll of tickets that Anderson and Joanne sold?
Answer:
Given,
Anderson and Joanne sold tickets for the play. Anderson sold \(\frac{3}{4}\) of the roll of tickets, and Joanne sold \(\frac{1}{6}\) of the roll of tickets.
\(\frac{3}{4}\) – \(\frac{1}{6}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 12
\(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\)
So, the difference between the fractions of the roll of tickets that Anderson and Joanne sold is \(\frac{7}{12}\)
Turn and Talk How could you represent this problem using only \(\frac{1}{12}\)-fraction strips?
2. Two boxes have the same number of play programs. On the first night of the play, Diana handed out \(\frac{2}{3}\) of a box. On the second night, she handed out \(\frac{5}{12}\) of the other box. On which night did Diana hand out more programs? How much more of a fractional part of a box did she hand out?

Draw a visual model to represent the situation.

A. On which night did she hand out more programs? How do you know?
_______________________
_______________________
B. How much more of a fractional part of a box did she hand out? How does your visual model show this?
_______________________
_______________________
Answer:
Given,
Two boxes have the same number of play programs. On the first night of the play, Diana handed out \(\frac{2}{3}\) of a box.
On the second night, she handed out \(\frac{5}{12}\) of the other box.
\(\frac{2}{3}\) – \(\frac{5}{12}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 12.
\(\frac{8}{12}\) – \(\frac{5}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Check Understanding Math Board
Question 1.
Maria is in charge of the scenery for the play. She paints \(\frac{11}{12}\) of a board green or blue. If she paints \(\frac{1}{2}\) of the whole board blue, how much of the board that she paints is green? Draw a visual model to represent the situation.
Answer:
Given,
Maria is in charge of the scenery for the play.
She paints \(\frac{11}{12}\) of a board green or blue.
she paints \(\frac{1}{2}\) of the whole board blue
\(\frac{11}{12}\) – \(\frac{1}{2}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 12.
\(\frac{11}{12}\) – \(\frac{6}{12}\) = \(\frac{5}{12}\)
On Your Own
Question 2.
Use Structure Greta and Tran have the lead roles in the play. Greta is on stage for \(\frac{3}{4}\) of the play. Tran is on stage for \(\frac{2}{3}\) of the play. What is the difference between the fractions of the play that Greta and Tran each spend on stage? Draw a visual model to represent the difference.

____________
Answer:
Given,
Greta and Tran have the lead roles in the play.
Greta is on stage for \(\frac{3}{4}\) of the play.
Tran is on stage for \(\frac{2}{3}\) of the play.
\(\frac{3}{4}\) – \(\frac{2}{3}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 12.
\(\frac{9}{12}\) – \(\frac{8}{12}\) = \(\frac{1}{12}\)
Thus the difference between the fractions of the play that Greta and Tran each spend on stage is \(\frac{1}{12}\).
Use Tools Use a visual model to find the difference.
Question 3.
\(\frac{11}{12}\) – \(\frac{2}{3}\) = ____
Answer:
\(\frac{11}{12}\) – \(\frac{2}{3}\)
The denominator of both the fractions are not same we have to make the common denominators.
\(\frac{11}{12}\) – \(\frac{2}{3}\)
LCD is 12.
\(\frac{11}{12}\) – \(\frac{8}{12}\) = \(\frac{3}{12}\)
Question 4.
\(\frac{3}{5}\) – \(\frac{3}{10}\) = ____
Answer:
\(\frac{3}{5}\) – \(\frac{3}{10}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 10
\(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\)
Question 5.
\(\frac{9}{8}\) – \(\frac{1}{4}\) = ____
Answer:
\(\frac{9}{8}\) – \(\frac{1}{4}\)
The denominator of both the fractions are not same we have to make the common denominators.
LCD is 8.
\(\frac{9}{8}\) – \(\frac{2}{8}\) = \(\frac{7}{8}\)
Question 6.
Hannah prints t-shirts for everyone working on the play. Her printing machine uses \(\frac{1}{2}\) milliliter of ink for each shirt. The front of each shirt uses \(\frac{2}{5}\) milliliter of ink. How much ink does the printer use for the back of each shirt?

Answer:
Given,
Hannah prints t-shirts for everyone working on the play. Her printing machine uses \(\frac{1}{2}\) milliliter of ink for each shirt.
The front of each shirt uses \(\frac{2}{5}\) milliliter of ink.
\(\frac{1}{2}\) – \(\frac{2}{5}\)
LCD is 10
\(\frac{5}{10}\) – \(\frac{4}{10}\) = \(\frac{1}{10}\)
Thus the printer use \(\frac{1}{10}\) milliliter of ink for the back of each shirt
I’m in a Learning Mindset!
What would I like to learn more about when I am studying how to use visual models to subtract fractions with different-sized parts?
_______________________________
Answer:
A fraction area model shows a whole shape split into equal parts. Equivalent fractions are ways of describing the same amount by using different-sized fractional parts.