We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 2 Join Parts of the Same Whole to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 2 Answer Key Join Parts of the Same Whole
I Can use fraction models to solve problems and describe joining fractions with like denominators.
Spark Your Learning
Terrell is making berry muffins using the recipe shown. How many cups of berries does Terrell need?

Show your thinking.
Answer:
\(\frac{5}{6}\)
Explanation:
\(\frac{3}{6}\) of straw berries
\(\frac{2}{6}\) of blue berries
cups of berries does Terrell need is
\(\frac{3}{6}\) +\(\frac{2}{6}\) = \(\frac{5}{6}\)
Turn and Talk How do you know your answer is reasonable?
Answer:
Terrell is making berry muffins using the recipe shown in the above picture.
Explanation:
To make muffins he need the following ingredients
\(\frac{3}{6}\) of straw berries
\(\frac{2}{6}\) of blue berries
Number of cups he prepare \(\frac{3}{6}\) +\(\frac{2}{6}\) = \(\frac{5}{6}\)
Build Understanding
Question 1.
A recipe calls for the amounts of brown sugar and white sugar shown. How many cups of sugar are needed?

Draw a representation of each fraction in the problem. Then represent the total amount of sugar needed.
Answer:
\(\frac{5}{8}\)
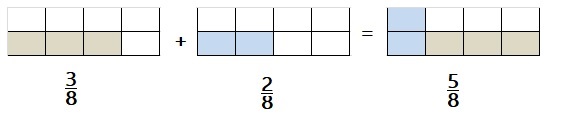
Explanation:
\(\frac{3}{8}\) of brown sugar
\(\frac{2}{8}\) of white sugar
Number of cups of sugar needed \(\frac{3}{8}\) +\(\frac{2}{8}\) = \(\frac{5}{8}\)
A. How does your drawing show the total amount of sugar needed?
Answer:

Explanation:
Total sugar = Brown sugar + White sugar
\(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\)
B. Why are you able to join together the pieces from each fraction to solve the problem?
Answer:
Two fraction are to be joined to get total quantity of sugar required as shown above.
Explanation:
\(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\)
C. What addition equation can you write to model the total amount of sugar needed?
Answer:
\(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\)
Explanation:
let s is the total amount of sugar needed = Brown sugar + White sugar
s = \(\frac{3}{8}\) + \(\frac{2}{8}\)
s = \(\frac{5}{8}\)
Turn and Talk How does your equation represent joining together of same-sized pieces?
Answer:
s = \(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\)
Explanation:
In both sugars the whole is divided into 8 equal parts.
So, due to the equal fractions the denominator is same,
then the equation represent joining together of same-sized pieces
let s = the total amount of sugar needed
s = \(\frac{3}{8}\) + \(\frac{2}{8}\)
s = \(\frac{5}{8}\)
Step It Out
Question 2.
A recipe calls for milk and oil. Terrell measures the milk and the oil as shown. He then pours both into a mixing bowl. How many cups of liquid ingredients does Terrell now have in the bowl?
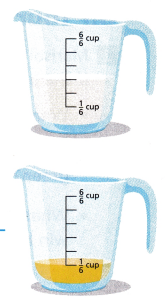
A. Write an equation to model the situation. Use c for the total cups of liquid in the bowl.
Answer:
c = \(\frac{4}{6}\)
Explanation:
c is the total cups of liquid in the bowl
c = milk + oil
c = \(\frac{3}{6}\) + \(\frac{1}{6}\)
c = \(\frac{4}{6}\)
B. Represent the amount of milk and oil using fraction models. Join together same-sized pieces to find the total amount of liquid ingredients. Draw a visual representation of your solution.
Answer:
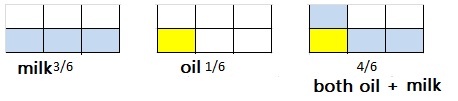
C. Rewrite your equation from Part A by replacing c with the total amount of liquid.
Answer:
c = \(\frac{4}{6}\)
Explanation:
c = milk + oil
c = \(\frac{3}{6}\) + \(\frac{1}{6}\)
c = \(\frac{4}{6}\)
Check Understanding
Question 1.
Lora walks \(\frac{3}{10}\) mile on the first day and \(\frac{2}{10}\) mile on the next. How far does she walk during the two days? Draw a fraction model to solve.
Lora walks __________ mile.
Answer:
Lora walks \(\frac{1}{2}\) mile
Explanation:
Lora walks
\(\frac{3}{10}\) mile on the first day
\(\frac{2}{10}\) mile on the second day.
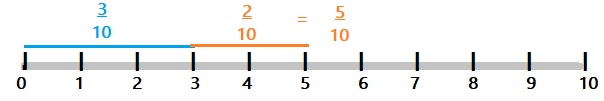
let ‘d’ is the far does she walk during the two days
\(\frac{3}{10}\) + \(\frac{2}{10}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)
On Your Own
Question 2.
Marisol is playing a game with this spinner. If the pointer lands on yellow or green, she wins.

What fraction represents the part of the spinner that is yellow? What fraction represents the part that is green?
Answer:
\(\frac{1}{6}\)
Explanation:
fraction represents the part of the spinner that is yellow
\(\frac{2}{12}\) = \(\frac{1}{6}\)
fraction represents the part of the spinner that is green
\(\frac{2}{12}\) = \(\frac{1}{6}\)
What fraction of the whole spinner would allow Marisol to win her game? Explain.
Answer:
\(\frac{1}{3}\)
Explanation:
fraction represents the part of the spinner that is yellow
\(\frac{2}{12}\) = \(\frac{1}{6}\)
fraction represents the part of the spinner that is green
\(\frac{2}{12}\) = \(\frac{1}{6}\)
fraction represents the part of the spinner that is yellow + green
\(\frac{2}{12}\) + \(\frac{2}{12}\)
= \(\frac{2+2}{12}\)
= \(\frac{4}{12}\)
= \(\frac{1}{3}\) the pointer lands on yellow or green, she wins
Question 3.
Critique Reasoning Tom eats \(\frac{1}{8}\) loaf of bread. Dana eats 1 loaf more than Tom eats. Julia says Dana eats \(\frac{1}{8}\) of a loaf. Is Julia correct? Explain. Use visual models to justify your answer.
Answer:
Julia not correct
Explanation:
Tom eats \(\frac{1}{8}\) loaf of bread
Dana eats 1 loaf more than Tom eats = \(\frac{2}{8}\)
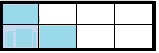
Complete the equation.
Question 4.
3 tenths + 5 tenths = __________
Answer:
8 tenths
Explanation:
Whole is divided into 10 equal parts.
\(\frac{3}{10}\) \(\frac{5}{10}\) = \(\frac{8}{10}\)
Question 5.
1 third + 1 third = __________
Answer:
2 third
Explanation:
Whole is divided into 3 equal parts.
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)
I’m in a Learning Mindset!
How can I keep myself on task when solving addition problems involving fractions?
Answer:
Make sure the denominators are the same.
Add the numerators and put that answer over the denominator.
Simplify the fraction.
Example;
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)