We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 3 Represent Addition of Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 3 Answer Key Represent Addition of Fractions
I Can use visual representations to add fractions. I can write equations to model a given number line or word problem.
Spark Your Learning
Caleb enters a frog in a frog-jumping contest. His frog jumps twice. Caleb wants to find the total distance his frog jumps.
Explain how can you determine the lengths of each of the frog’s two jumps, then find the total distance the frog jumped.
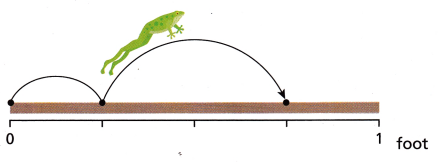
Answer:
\(\frac{3}{4}\)
Explanation:
In the first jump it jumps \(\frac{1}{4}\)
In the second jump it jumps \(\frac{2}{4}\)
Total distance the frog jumped in both the jumps
\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)
Turn and Talk How does the visual representation support your answer?
Answer:
Frog jumped in two steps
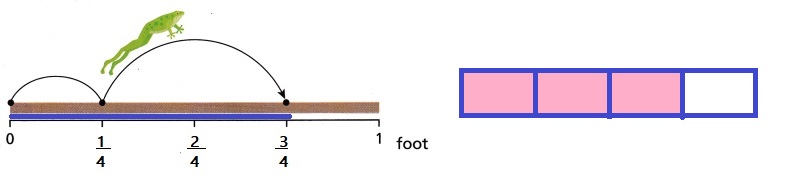
the total distance the frog jumped.
\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)
Explanation:
Visual representation clearly shows the distance jumped by the frog.
Distance is equally divided into 4 parts,
in first jump it is \(\frac{1}{4}\) and in second jump it is \(\frac{2}{4}\)
Total distance the frog jumped in both the jumps
\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)
Build Understanding
Question 1.
A grasshopper jumps \(\frac{2}{6}\) yard and then immediately jumps another \(\frac{3}{6}\) yard. How far does the grasshopper jump?
Represent the jumps on the number line.
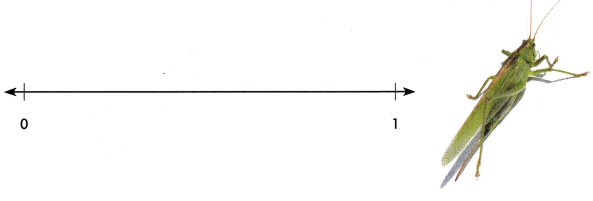
A. What addition equation can you write to model the distance the grasshopper jumps?
Answer:
\(\frac{2}{6}\) + \(\frac{3}{6}\)
= \(\frac{2 + 3 }{6}\)
=\(\frac{5}{6}\)
B. How does your equation relate to what you drew on the number line?
Answer:

C. The grasshopper jumps a total of _________ yard.
Answer:
\(\frac{5}{6}\)
D. What do you notice about the numerators and denominators of the addends and the numerator and denominator of the sum?
Answer:
The numerators of the addends are different where as the denominators of the addends are same.
Explanation:
Sum of the addends \(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
Turn and Talk How could you have solved the problem without using a number line to represent the problem?
Answer:
With out using the number line, we use the second number to count with the first number as the reference. When we add two numbers we get the sum of the addends or numbers.
Step It Out
Question 2.
Sam’s pet rabbit lives in a hutch with a sleeping space that has an area of \(\frac{3}{12}\) square yard. Cici’s pet rabbit has a sleeping space that has an area that is \(\frac{4}{12}\) square yard larger than Sam’s rabbit’s sleeping space. What is the area of Cici’s rabbit’s sleeping space?

A. Use the visual fraction model to find the area of Cici’s rabbit’s sleeping space.
Shade the fractions strips that represent the area of the sleeping space for Sam’s rabbit. Use a different color to shade how much bigger the area of Cici’s rabbit’s sleeping space is.
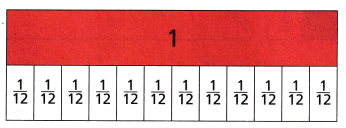
Answer:
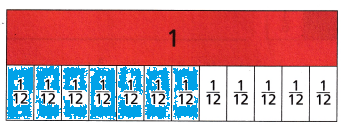
B. Write an addition equation to model the area of Cici’s rabbit’s sleeping space, s.
Answer:
\(\frac{7}{10}\)
C. What is the area of Cici’s rabbit’s sleeping space?
Answer:
s = \(\frac{3}{12}\) + \(\frac{4}{12}\) = \(\frac{7}{10}\)
Explanation:
Sam’s pet rabbit lives in a hutch with a sleeping space that has an area of \(\frac{3}{12}\) square yard. Cici’s pet rabbit has a sleeping space that has an area that is \(\frac{4}{12}\) square yard larger than the area of Cici’s rabbit’s sleeping space \(\frac{3}{12}\)+\(\frac{4}{12}\)=\(\frac{7}{10}\)
Check Understanding
Question 1.
Use the number line to find the sum.
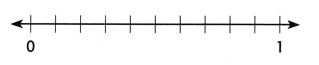
\(\frac{4}{10}\) + \(\frac{4}{10}\) = _________
Answer:
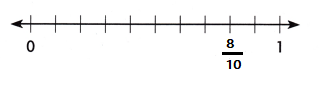
Explanation:
Whole is divided into 10 equal parts,
Sum of 2 parts of whole is \(\frac{8}{10}\)
\(\frac{4}{10}\) + \(\frac{4}{10}\) = \(\frac{8}{10}\)
Find the sum.
Question 2.
\(\frac{1}{4}\) + \(\frac{1}{4}\) = _________
Answer:
\(\frac{2}{4}\)
Explanation:
Whole is divided into 4 equal parts,
Sum of the whole is \(\frac{2}{4}\)
\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
Question 3.
\(\frac{1}{8}\) + \(\frac{2}{8}\) = ________
Answer:
\(\frac{3}{8}\)
Explanation:
Whole is divided into 8 equal parts.
Sum of the two fractions of whole is \(\frac{3}{8}\)
\(\frac{1}{10}\) + \(\frac{2}{8}\) = \(\frac{3}{8}\)
On Your Own
Question 4.
Model with Mathematics Weston walks \(\frac{1}{4}\) mile to school and \(\frac{1}{4}\) mile home. How many miles does Weston walk? Use a visual fraction model, write an equation, and find the distance, d.

Answer:
\(\frac{2}{4}\)

Explanation:
Weston walks \(\frac{1}{4}\) mile to school and
\(\frac{1}{4}\) mile home.
Total miles Weston walk = \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
Question 5.
Use Structure Judy uses these fraction strips to find a sum. What are two equations that could model this sum?
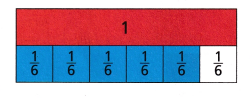
Answer:
\(\frac{5}{6}\)
Explanation:
The sum of the addends \(\frac{3}{6}\) + \(\frac{2}{6}\) = \(\frac{5}{6}\)
Question 6.
Max spends \(\frac{1}{5}\) hour sweeping the floor, It takes \(\frac{3}{5}\) hour more to clean his room than to sweep the floor. How many hours does Max spend cleaning his room? Explain your answer.
Answer:
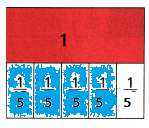
Explanation:
Max spends \(\frac{1}{5}\) hour sweeping the floor,
It takes \(\frac{3}{5}\) hour more to clean his room than to sweep the floor.
Total hours Max spend cleaning his room = \(\frac{4}{5}\) hour
Find the sum.
Question 7.
\(\frac{5}{10}\) + \(\frac{4}{10}\) = ___________
Answer:
\(\frac{9}{10}\)
Explanation:
whole is divided into 10 equal parts,
sum of the fractions of whole,
\(\frac{5}{10}\) + \(\frac{4}{10}\) = \(\frac{9}{10}\)
Question 8.
\(\frac{2}{8}\) + \(\frac{5}{8}\) = ___________
Answer:
\(\frac{7}{8}\)
Explanation:
whole is divided into 8 equal parts,
sum of the fractions of whole,
\(\frac{2}{8}\) + \(\frac{5}{8}\) = \(\frac{7}{8}\)
Question 9.
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{2}{6}\) = ___________
Answer:
\(\frac{4}{6}\)
Explanation:
whole is divided into 6 equal parts,
sum of the fractions of whole,
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{4}{6}\)
Question 10.
\(\frac{3}{8}\) + \(\frac{1}{8}\) + \(\frac{3}{8}\) = ___________
Answer:
\(\frac{7}{8}\)
Explanation:
whole is divided into 8 equal parts,
sum of the fractions of whole,
\(\frac{3}{8}\) + \(\frac{1}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)
I’m in a Learning Mindset!
What types of decisions did I make when solving problems involving addition of fractions?
Answer:
Make sure that the denominators of fractions should be same.
Explanation:
The denominators are the same than add the numerators.
Simplify the fraction if possible.