We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 1 Decompose Fractions into Sums to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 1 Answer Key Decompose Fractions into Sums
I Can decompose visual fraction models into sums and model the decomposition with addition equations.
Spark Your Learning
Meghan, Zoe, Jack, and Gabriel are sharing these pieces of watermelon. Some of the friends like watermelon more than others. Meghan wants to eat the most pieces of watermelon. Jack wants to eat the same number of pieces as Gabriel. Zoe wants to eat more pieces than Gabriel.
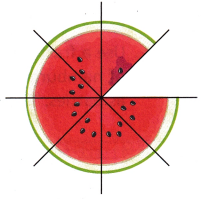
How can you represent the amount of watermelon each person will receive if they eat the rest of the watermelon?
Show your thinking.
Answer:
\(\frac{1}{8}\)
Explanation:
Whole is divided into 8 equal parts,
each fraction of whole is \(\frac{1}{8}\)
Turn and Talk How could you model the situation with an equation?
Answer:
Meghan, Zoe, Jack, and Gabriel are sharing these pieces of watermelon
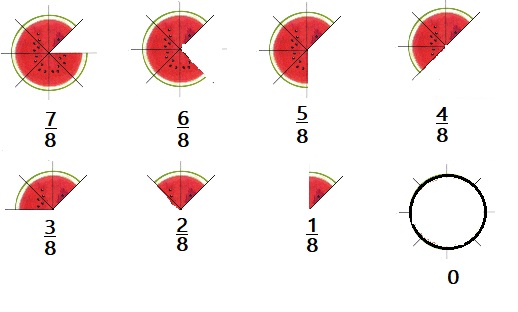
Explanation:
Whole is divided into 8 equal parts,
each fraction of whole is \(\frac{1}{8}\)
Meghan, Zoe, Jack, and Gabriel are sharing these pieces of watermelon
\(\frac{1}{8}\); \(\frac{2}{8}\); \(\frac{3}{8}\)
\(\frac{4}{8}\); \(\frac{5}{8}\);\(\frac{6}{8}\); \(\frac{7}{8}\)
Build Understanding
Question 1.
Tony and his family visit a state park. They grill \(\frac{5}{6}\) pound of hamburger for lunch. The hamburger is made into \(\frac{1}{6}\)-pound patties. How many hamburger patties do Tony and his family have?

Answer:
5 hamburger patties
Explanation:
Tony family members are 5
Each hamburger is made into \(\frac{1}{6}\)-pound patties
Hamburger grilled for lunch = \(\frac{5}{6}\)
A. Use a fraction model to represent the amount of hamburger Tony and his family have to grill as patties. The whole represents 1 pound.
Answer:
Explanation:
Whole is divided into 6 parts,
fraction of whole is \(\frac{1}{6}\)
5 x \(\frac{1}{6}\) = \(\frac{5}{6}\)
Connect to Vocabulary
A unit fraction tells the part of a whole that each piece represents. The numerator of a unit fraction is always 1.
B. What does each unit fraction represent in the problem?
Answer:
Part of of whole is fraction
C. What addition equation can you write to model the weight of hamburger as a sum of the weight of the patties?
Answer:
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
= \(\frac{5}{6}\)
Explanation:
Whole is divided into 6 parts,
fraction of whole is \(\frac{1}{6}\)
D. How many \(\frac{1}{6}\)-pound hamburger patties do Tony and his family have?
Answer:
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
= \(\frac{5}{6}\)
Explanation:
Whole is divided into 6 parts,
fraction of whole is \(\frac{1}{6}\)
Turn and Talk If there are 3 people in Tony’s family including Tony and each person eats at least one patty, how can you model the total amount of hamburger they eat with an addition equation?
Answer:
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{3}{6}\)
Explanation:
Whole is divided into 6 parts,
fraction of whole is \(\frac{1}{6}\)
Number of peole in Tonys family are 3.
So, the hamburger used = \(\frac{3}{6}\)
Question 2.
Tony and his family drove \(\frac{7}{12}\) of the distance across Michigan on Saturday. What are three ways they could break up the drive into 2 parts so that they could stop and walk their dog?
Shade the visual fraction models to show how they could break up the drive. Then model each with an equation.
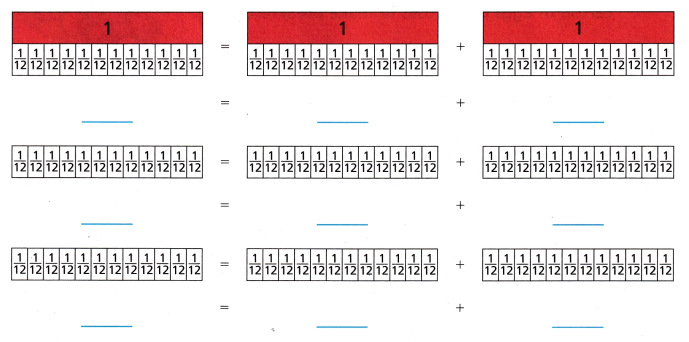
Answer:
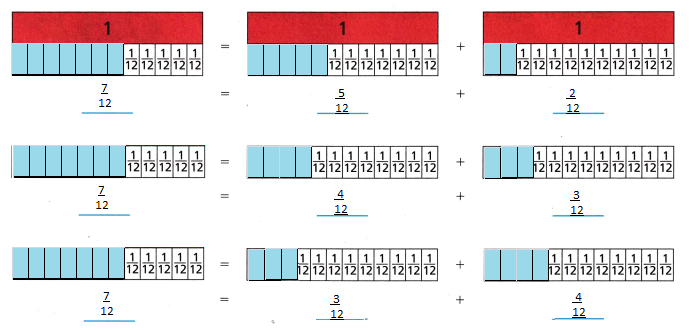
Explanation:
From the above information the whole is divided into 12 equal parts,
Tony and his family drove \(\frac{7}{12}\) of the distance across Michigan on Saturday.
The 3 ways are shown in visual representation.
Turn and Talk How do you know that your visual fraction models and equations correctly represent a solution to the problem?

\(\frac{7}{12}\) = \(\frac{5}{12}\) + \(\frac{2}{12}\)
\(\frac{7}{12}\) = \(\frac{4}{12}\) + \(\frac{3}{12}\)
\(\frac{7}{12}\) = \(\frac{3}{12}\) + \(\frac{4}{12}\)
Explanation:
The denominator cuts a whole into equal parts.
The numerator counts those parts travelled by Tony and his family.
Check Understanding
Question 1.
Write \(\frac{4}{6}\) as the sum of unit fractions.
Answer:
\(\frac{4}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) \(\frac{1}{6}\)
Explanation:
The whole is divided into 6 parts,
there are \(\frac{4}{6}\) unit fractions.
Write the fraction as the sum of two fractions.
Question 2.
\(\frac{4}{10}\) = ___________
Answer:
\(\frac{4}{10}\) = \(\frac{2}{10}\) + \(\frac{2}{10}\)
Explanation:
The whole is is divided into 10 equal parts.
sum of the two fractions are \(\frac{2}{10}\) + \(\frac{2}{10}\) = \(\frac{4}{10}\)
Question 3.
\(\frac{5}{100}\) = ___________
Answer:
\(\frac{5}{100}\) = \(\frac{3}{100}\) + \(\frac{2}{100}\)
Explanation:
The whole is is divided into 100 equal parts.
sum of the two fractions are \(\frac{3}{10}\) + \(\frac{2}{10}\) = \(\frac{5}{10}\)
On Your Own
Question 4.
Model with Mathematics Carlos buys this carton of eggs. He uses 5 eggs to make breakfast for himself and his sister.

Draw a fraction model to show the fraction of the carton of eggs Carlos uses to make breakfast.
Answer:
Explanation:
The whole is equally into 12 parts,
Carlos uses parts of it.
What addition equations can you write to model the fraction of the carton of eggs Carlos eats and the fraction his sister eats?
Answer:
\(\frac{5}{12}\) = \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) OR
\(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)
Explanation:
There are total 12 eggs in a cartoon.
out of which 5 eggs are used by Carlos and his sister.
Write the fraction as the sum of unit fractions.
Question 5.
\(\frac{2}{3}\) = __________
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\)
Explanation:
We break apart the fractions into addends that are unit fractions.
Whole is divided into 3 equal parts, with 2 unit fractions.
Question 6.
\(\frac{3}{4}\) = ___________
Answer:
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
Explanation:
We break apart the fractions into addends that are unit fractions.
Whole is divided into 4 equal parts, with 3 unit fractions.
Question 7.
\(\frac{4}{5}\) = ___________
Answer:
\(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
Explanation:
We break apart the fractions into addends that are unit fractions.
Whole is divided into 5 equal parts, with 4 unit fractions.
Question 8.
Model with Mathematics Erin and three friends equally share the rest of the pie shown. What fraction of the whole pie do Erin and her friends eat? Write an equation to justify your answer.
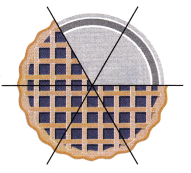
Answer:
\(\frac{2}{3}\)
Explanation:
Whole ids divided into 6 equal parts, fraction of whole is \(\frac{1}{6}\)
\(\frac{1}{6}\) + \(\frac{1}{6}\) +\(\frac{1}{6}\)+ \(\frac{1}{6}\)
= \(\frac{4}{6}\)
Simplifying \(\frac{4}{6}\) we get \(\frac{2}{3}\)
Question 9.
Use Structure Write the fraction \(\frac{6}{8}\) as a sum of two fractions in three different ways.
Answer:
\(\frac{6}{8}\) = \(\frac{4}{8}\) + \(\frac{2}{8}\)
\(\frac{6}{8}\) = \(\frac{3}{8}\) + \(\frac{3}{8}\)
\(\frac{6}{8}\) = \(\frac{5}{8}\) + \(\frac{1}{8}\)
Explanation:
Whole is divided into 8 equal parts and sum of the two fractions are shown in 3 different ways in the above.
The sum of the fractions are \(\frac{6}{8}\)
I’m in a Learning Mindset!
What strategies can I use to write fractions as a sum of fractions?
Answer:
We add the numerators and use their common denominators.
We break apart the fractions into addends that are unit fractions.
Explanation:
For example;
\(\frac{2}{8}\) + \(\frac{1}{8}\) = \(\frac{3}{8}\)
\(\frac{2}{7}\) = \(\frac{1}{7}\) + \(\frac{1}{7}\)