We included HMH Into Math Grade 4 Answer Key PDF Module 11 Lesson 5 Common Multiples to Write Equivalent Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 11 Lesson 5 Answer Key Common Multiples to Write Equivalent Fractions
I Can use common multiples to rewrite two fractions so they have a common denominator or a common numerator.

Connect to Vocabulary
A common multiple is a number that is a multiple of two or more numbers. A common denominator is a common multiple of the denominators of two or more fractions.
Step It Out
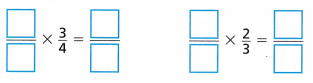
1. Sam needs \(\frac{3}{4}\) cup of bananas and \(\frac{2}{3}\) cup of strawberries for a recipe. How can he write \(\frac{3}{4}\) and \(\frac{2}{3}\) as a pair of fractions with a common denominator?
A common multiple can be used as a common denominator.
A. List the first 5 multiples of each denominator.
Multiples of 4: ____
Multiples of 3: ____
B. Choose a common multiple. List more multiples, if needed. Then use multiplication to determine the relationship between each denominator and the common multiple you chose.
________________________
________________________
C. Use the relationships between the denominators and the common multiple to write equivalent fractions.
Answer:
He can \(\frac{3}{4}\) and \(\frac{2}{3}\) as a pair of fractions with a common denominator as \(\frac{9}{12}\) \(\frac{8}{12}\).
Explanation:
Number of cup of bananas for a recipe Sam needs = \(\frac{3}{4}\)
Number of cup of strawberries for a recipe Sam needs = \(\frac{2}{3}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 4 n 3 = 12.
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
Turn and Talk What do you know about two fractions that have a common denominator?
Answer:
When the denominators of two or more fractions are the same, they are Common Denominators.
Explanation:
When the denominators of two or more fractions are the same, they are Common Denominators. While performing arithmetic operations such as addition and subtraction, if the denominators of the fractions are common or equal, then it becomes easy to add or subtract them.
Step It Out
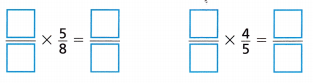
2. Alison needs \(\frac{5}{8}\) cup of almonds and \(\frac{4}{5}\) cup of walnuts for a recipe. How can she write \(\frac{5}{8}\) and \(\frac{4}{5}\) as a pair of fractions with a common numerator?

A common multiple can be used as a common numerator.
A. List multiples of each numerator until you find a common multiple.
Multiples of 5: ____
Multiples of 4: _____
B. Use multiplication to determine the relationship between each numerator and the common multiple you chose.
__________________
C. Use the relationships between the numerators and the common multiple to write equivalent fractions.
________________________
Answer:
She can write \(\frac{5}{8}\) and \(\frac{4}{5}\) as a pair of fractions with a common numerator as \(\frac{20}{32}\) and \(\frac{20}{25}\).
Explanation:
Number of cups of almonds Alison needs for a recipe = \(\frac{5}{8}\)
Number of cups of walnuts Alison needs for a recipe = \(\frac{4}{5}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Common multiple of 5 n 4 = 20.
\(\frac{5}{8}\) = \(\frac{5}{8}\) × \(\frac{4}{4}\) = \(\frac{20}{32}\)
\(\frac{4}{5}\) = \(\frac{4}{5}\) × \(\frac{5}{5}\) = \(\frac{20}{25}\)
Turn and Talk How could you use the denominators to compare two fractions with the same numerators?
Answer:
When two fractions have the same denominator, you can compare which fraction is greater by just comparing the numerators.
Explanation:
When two fractions have the same denominator, you can compare which fraction is greater by just comparing the numerators. For example, if you have 2/5 and 3/5, the denominators are the same. So you can just look at the numerators. 3 is greater than 5, so 3/5 is greater than 2/5.
Check Understanding Math Board
Write the pair of fractions as a pair of fractions with a common denominator or common numerator.
Question 1.
\(\frac{1}{3}\) and \(\frac{2}{5}\)
Answer:
\(\frac{1}{3}\) and \(\frac{2}{5}\) as a pair of fractions with a common denominator as \(\frac{5}{15}\) and \(\frac{6}{15}\).
Explanation:
\(\frac{1}{3}\) and \(\frac{2}{5}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 5 n 4 = 20.
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{5}{5}\) = \(\frac{5}{15}\)
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{3}{3}\) = \(\frac{6}{15}\)
\(\frac{5}{15}\) < \(\frac{6}{15}\)
Question 2.
\(\frac{3}{4}\) and \(\frac{5}{8}\)
Answer:
\(\frac{3}{4}\) and \(\frac{5}{8}\) as a pair of fractions with a common denominator as
\(\frac{12}{16}\) and \(\frac{10}{16}\)
Explanation:
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 4 n 8 = 16.
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{4}{4}\) = \(\frac{12}{16}\)
\(\frac{5}{8}\) = \(\frac{5}{8}\) × \(\frac{2}{2}\) = \(\frac{10}{16}\)
\(\frac{12}{16}\) > \(\frac{10}{16}\)
Question 3.
\(\frac{2}{5}\) and \(\frac{3}{8}\)
Answer:
\(\frac{2}{5}\) and \(\frac{3}{8}\) as a pair of fractions with a common numerator as
\(\frac{6}{15}\) and \(\frac{6}{16}\)
Explanation:
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 2 n 3 = 6.
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{3}{3}\) = \(\frac{6}{15}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\) × \(\frac{2}{2}\) = \(\frac{6}{16}\)
\(\frac{6}{15}\) > \(\frac{6}{16}\)
On Your Own
Question 4.
Critique Reasoning Jerry has two same-sized circles divided into the same number of equal parts. One circle has \(\frac{3}{4}\) of the parts shaded, and the other has \(\frac{2}{3}\) of the parts shaded. His sister says that the least number of pieces each circle could be divided into is 7. Is his sister correct? Explain.
Answer:
His sister is incorrect because least shaded parts are having total 3 not 7 parts, which means each circle cannot be divided into 7.
Explanation:
Shaded part on one circle = \(\frac{3}{4}\)
Shaded part on other circle = \(\frac{2}{3}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 4 n 3 = 12.
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
\(\frac{9}{12}\) < \(\frac{8}{12}\)
Least pieces circle = Shaded part on other circle = \(\frac{2}{3}\)
Question 5.
Reason Magara was working on her math homework when she spilled orange juice on her paper. She wrote two pairs of equivalent fractions. What is the unknown numerator covered by the juice?
The unknown numerator is ____.
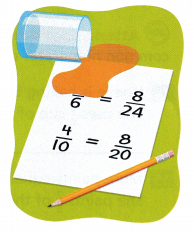
Answer:
The unknown numerator is 2 \(\frac{2}{6}\).
Explanation:
One pair of fraction = \(\frac{??}{6}\) = \(\frac{8}{24}\)
Other pair of fraction = \(\frac{4}{10}\) = \(\frac{8}{20}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
\(\frac{??}{6}\) = \(\frac{??}{6}\) × \(\frac{4}{4}\) = \(\frac{8}{24}\)
=> \(\frac{??}{6}\) = \(\frac{2}{6}\) × \(\frac{4}{4}\) = \(\frac{8}{24}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\) × \(\frac{2}{2}\) = \(\frac{8}{20}\)
Write the pair of fractions as a pair of fractions with a common denominator.
Question 6.
\(\frac{1}{4}\) and \(\frac{5}{6}\)
Answer:
\(\frac{1}{4}\) and \(\frac{5}{6}\) as a pair of fractions with a common denominator as \(\frac{3}{12}\) and \(\frac{10}{12}\)
Explanation:
\(\frac{1}{4}\) and \(\frac{5}{6}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 4 n 6 = 12.
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{3}{3}\) = \(\frac{3}{12}\)
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
\(\frac{3}{12}\) < \(\frac{10}{12}\)
Question 7.
\(\frac{3}{5}\) and \(\frac{4}{10}\)
Answer:
\(\frac{3}{5}\) and \(\frac{4}{10}\) as a pair of fractions with a common denominator as
\(\frac{6}{10}\) and \(\frac{4}{10}\)
Explanation:
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 5 n 10 = 10.
\(\frac{3}{5}\)= \(\frac{3}{5}\)× \(\frac{2}{2}\) = \(\frac{6}{10}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\) × \(\frac{1}{1}\) = \(\frac{4}{10}\)
\(\frac{6}{10}\) > \(\frac{4}{10}\)
Write the pair of fractions as a pair of fractions with a common numerator.
Question 8.
\(\frac{1}{6}\) and \(\frac{5}{8}\)
Answer:
\(\frac{1}{6}\) and \(\frac{5}{8}\) as a pair of fractions with a common numerator as \(\frac{5}{30}\) and \(\frac{5}{8}\)
Explanation:
\(\frac{1}{6}\) and \(\frac{5}{8}\)
Multiples of 1: 1,2,3,4,5,6,7,8,9,10.
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Common multiple of 1 n 5 = 5.
\(\frac{1}{6}\) = \(\frac{1}{6}\) × \(\frac{5}{5}\) = \(\frac{5}{30}\)
\(\frac{5}{8}\) = \(\frac{5}{8}\) × \(\frac{1}{1}\) = \(\frac{5}{8}\)
\(\frac{5}{30}\) > \(\frac{5}{8}\)
Question 9.
\(\frac{2}{3}\) and \(\frac{5}{6}\)
Answer:
\(\frac{2}{3}\) and \(\frac{5}{6}\) as a pair of fractions with a common numerator as
\(\frac{10}{15}\) and \(\frac{10}{12}\)
Explanation:
\(\frac{2}{3}\) and \(\frac{5}{6}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Common multiple of 5 n 2 = 10.
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{5}{5}\) = \(\frac{10}{15}\)
\(\frac{5}{6}\) =\(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
\(\frac{10}{15}\) < \(\frac{10}{12}\)
On Your Own
Find a common denominator for the pair of fractions.
Question 10.
\(\frac{1}{5}\) and \(\frac{1}{8}\)
Answer:
40 is the common denominator for the pair of fractions \(\frac{1}{5}\) and \(\frac{1}{8}\)
Explanation:
\(\frac{1}{5}\) and \(\frac{1}{8}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 5 n 8 = 40.
\(\frac{1}{5}\) = \(\frac{1}{5}\) × \(\frac{8}{8}\) = \(\frac{8}{40}\)
\(\frac{1}{8}\) = \(\frac{1}{8}\) × \(\frac{5}{5}\) = \(\frac{5}{40}\)
\(\frac{8}{40}\) > \(\frac{5}{40}\)
Question 11.
\(\frac{2}{5}\) and \(\frac{1}{2}\)
Answer:
10 is the common denominator for the pair of fractions \(\frac{2}{5}\) and \(\frac{1}{2}\)
Explanation:
\(\frac{2}{5}\) and \(\frac{1}{2}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Common multiple of 5 n 2 = 10.
\(\frac{2}{5}\)= \(\frac{2}{5}\)× \(\frac{2}{2}\) = \(\frac{4}{10}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{5}{5}\) = \(\frac{5}{10}\)
\(\frac{4}{10}\) < \(\frac{5}{10}\)
Question 12.
\(\frac{2}{4}\) and \(\frac{5}{6}\)
Answer:
12 is the common denominator for the pair of fractions \(\frac{2}{4}\) and \(\frac{5}{6}\)
Explanation:
\(\frac{2}{4}\) and \(\frac{5}{6}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 4 n 6 = 12.
\(\frac{2}{4}\) = \(\frac{2}{4}\) × \(\frac{3}{3}\) = \(\frac{6}{12}\)
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
\(\frac{6}{12}\) < \(\frac{10}{12}\)
Question 13.
Reason Nicholas wants to rewrite \(\frac{3}{5}\) and \(\frac{6}{12}\) so they have either the same numerator or the same denominator. Should he use a common numerator or a common denominator? Explain.
Answer:
He should use a common numerator than a common denominator.
Explanation:
Nicholas wants to rewrite \(\frac{3}{5}\) and \(\frac{6}{12}\)
Numerator = 3 n 6 = 6.
Denominator = 5 n 12.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 3 n 6 = 6.
Finding a common multiple for 3 n 6 is easy than 5 n 12.
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{2}{2}\) = \(\frac{6}{10}\)
\(\frac{6}{12}\) = \(\frac{6}{12}\) × \(\frac{1}{1}\) = \(\frac{6}{12}\)
Attend to Precision Rewrite the fractions so they have a common numerator or denominator.
Question 14.
Noelle is baking bread with her grandmother. She uses \(\frac{6}{8}\) cup of flour and \(\frac{2}{3}\) cup of sugar.
Answer:
\(\frac{6}{8}\) and \(\frac{2}{3}\) have a common numerator as \(\frac{6}{8}\) and \(\frac{6}{9}\)
Explanation:
Number of cups of flour she uses = \(\frac{6}{8}\)
Number of cups of sugar she uses = \(\frac{2}{3}\)
Numerators = 6 n 2
Denominators = 3 n 8
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Common multiple of 6 n 2 = 6.
\(\frac{6}{8}\) = \(\frac{6}{8}\) × \(\frac{1}{1}\) = \(\frac{6}{8}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{3}{3}\) = \(\frac{6}{9}\)
Question 15.
Mere paints equal sections of a wall to make a pattern. She paints \(\frac{2}{5}\) of the wall white and \(\frac{1}{2}\) of the wall lavender.

Answer:
\(\frac{2}{5}\) and \(\frac{1}{2}\) have a common numerator as \(\frac{6}{8}\) and \(\frac{1}{2}\)
Explanation:
Length of wall white she paints = \(\frac{2}{5}\)
Length of wall lavender she paints =\(\frac{1}{2}\)
Numerator = 2 n 1
Denominator = 5 n 2
Multiples of 1: 1,2,3,4,5,6,7,8,9,10.
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Common multiple of 1 n 2 = 2.
\(\frac{6}{8}\) = \(\frac{6}{8}\) × \(\frac{1}{1}\) = \(\frac{6}{8}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{3}{3}\) = \(\frac{6}{9}\)
Question 16.
Construct Arguments Koji says that to find a common denominator for any two fractions, you just need to multiply the two denominators of the fractions. Do you agree? Explain.
Answer:
No, I do not agree with Koji because he is not correct. To find a common denominator for ny two fractions, we should multiply the numerator n denominator of the fractions.
Explanation:
Koji says that to find a common denominator for any two fractions, you just need to multiply the two denominators of the fractions. Two fractions are equivalent fractions when they represent the same part of a whole. Since equivalent fractions do not always have the same numerator and denominator, one way to determine if two fractions are equivalent is to find a common denominator and rewrite each fraction with that denominator. Once the two fractions have the same denominator, you can check to see if the numerators are equal. If they are equal, then the two fractions are equal as well.