We included HMH Into Math Grade 4 Answer Key PDF Module 11 Lesson 4 Generate Equivalent Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 11 Lesson 4 Answer Key Generate Equivalent Fractions
I Can use multiplication and division to write fractions that are equivalent to a given fraction.
Step It Out
1. Karen is mixing organic fertilizer for a garden. She needs to add \(\frac{3}{4}\) teaspoon of fertilizer to water. But she only has a \(\frac{1}{8}\)-teaspoon measuring spoon. How many times does Karen need to fill the \(\frac{1}{8}\)-teaspoon measuring spoon?

A. You want to know how many eighths equal \(\frac{3}{4}\). Write the two fractions in an equation.
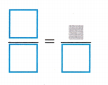
B. Use multiplication to determine the relationship between the two known denominators.
___________________________
___________________________
C. Use the relationship to find the unknown numerator for the equivalent fraction.
D. Karen needs to fill the \(\frac{1}{8}\)-teaspoon measuring spoon ___ times to measure \(\frac{3}{4}\) teaspoon.
Answer:
Karen needs to fill the \(\frac{1}{8}\)-teaspoon measuring spoon 6 times to measure \(\frac{3}{4}\) teaspoon.
Explanation:
Number of teaspoons of fertilizer to water she needs to add = \(\frac{3}{4}\)
Number of measuring spoon of fertilizer to water she has = \(\frac{1}{8}\)
Multiple of 4: 4,8,12,16,20,24,28,32,36,40.
Multiple of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 4 n 8 = 8.
\(\frac{3}{4}\) × \(\frac{2}{2}\) = \(\frac{6}{8}\)
Complete the visual models to justify your answer.

Step It Out
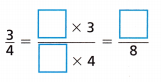
2. Use division to find an equivalent fraction for
A. Find the factors of 8 and 12.
- Factors of 8: ____
- Factors of 12: ____
Connect to Vocabulary
You previously learned about factors. A common factor is a factor of two or more numbers. You can use a common factor to divide the numerator and denominator to find an equivalent fraction.
B. Which are common factors of 8 and __________
C. Use a common factor other than 1 to find an equivalent fraction.
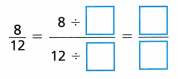
Complete the visual models to justify your answer.
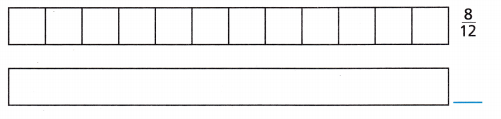
Answer:
\(\frac{8}{12}\) = \(\frac{2}{3}\)
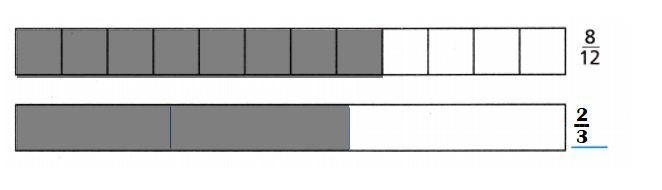
Explanation:
Multiple of 8: 8,16,24,32,40,48,56,64,72,80.
Multiples of 12: 12,24,36,48,60,72,84,96,108,12.
Common multiple of 8 n 12 = 24.
\(\frac{8}{12}\) = \(\frac{8}{12}\) ÷ \(\frac{2}{2}\)
= \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
Turn and Talk Why can two fractions have a different number and size of parts and still be equivalent fractions?
Answer:
Two fractions are equivalent to each other if after simplification either of two fractions is equal to the other one.
Two fractions are equivalent to each other if after simplification either of two fractions is equal to the other one.
Explanation:
Two fractions are equivalent to each other if after simplification either of two fractions is equal to the other one.
For example, ⅔ and 4/6 are equivalent fractions.
Since, 4/6 = (2×2)/(2×3) = 2/3.
Check Understanding Math Board
Question 1.
Rachel spends \(\frac{8}{10}\) hour in the garden. William spends \(\frac{4}{5}\) hour in the garden. Do Rachel and William spend the same amount of time in the garden? How do you know?

___________________________
___________________________
Answer:
Yes, Rachel and William spend the same amount of time in the garden because both their times are equal.
Explanation:
Number of hours Rachel spends in the garden = \(\frac{8}{10}\)
Number of hours William spends in the garden = \(\frac{4}{5}\)
\(\frac{8}{10}\) and \(\frac{4}{5}\)
\(\frac{8}{10}\) = \(\frac{8}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{4}{5}\)
Use multiplication or division to generate an equivalent fraction.
Question 2.
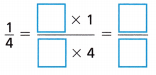
Answer:
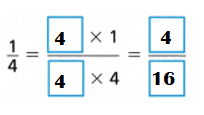
Explanation:
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 1: 1,2,3,4,5,6 ,7,8,9,10.
Common multiple of 1 n 4 = 4.
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{4}{4}\) = \(\frac{4}{16}\)
Question 3.
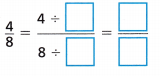
Answer:
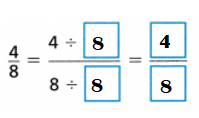
Explanation:
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 8: 8,16,24,32,40,48,56,64,7,80.
Common multiple of 4 n 8 = 8.
\(\frac{4}{8}\) = \(\frac{4}{8}\) ÷ \(\frac{8}{8}\) = \(\frac{4}{8}\) ÷ 1 = \(\frac{4}{8}\)
On Your Own
Question 4.
Use Tools Peter picks \(\frac{3}{5}\) pound of tomatoes. Explain how you can write an
equivalent fraction for \(\frac{3}{5}\). Use visual models to show how your fractions are equivalent.

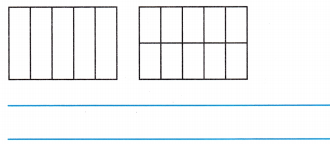
Answer:
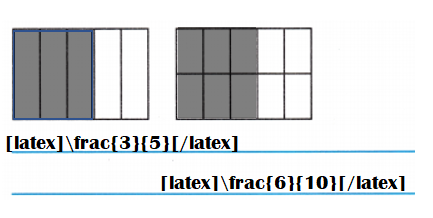
Explanation:
Number of pounds of tomatoes Peter picks = \(\frac{3}{5}\)
Equivalent fraction of \(\frac{3}{5}\):
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{2}{2}\) = \(\frac{6}{10}\)
Use multiplication or division to generate an equivalent fraction.
Question 5.
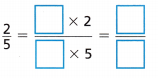
Answer:
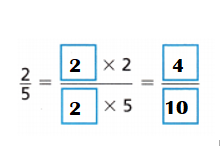
Explanation:
Equivalent fraction of \(\frac{2}{5}\):
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Common multiple of 2 n 5 = 10.
latex]\frac{2}{5}[/latex] = latex]\frac{2}{5}[/latex] × latex]\frac{2}{2}[/latex] = latex]\frac{4}{10}[/latex]
Question 6.
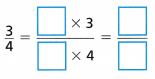
Answer:
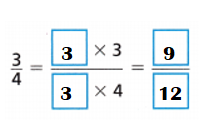
Explanation:
Equivalent fraction of \(\frac{3}{4}\):
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 3 n 4 = 12.
latex]\frac{3}{4}[/latex] = latex]\frac{3}{4}[/latex] × latex]\frac{3}{3}[/latex] = latex]\frac{9}{12[/latex]
Question 7.
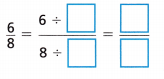
Answer:
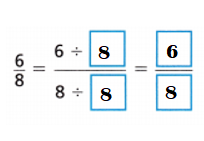
Explanation:
Equivalent fraction of \(\frac{6}{8}\):
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 8: 8,16,24,32,40,48,56,64,7,80.
Common multiple of 6 n 8 = 24.
latex]\frac{6}{8}[/latex] = latex]\frac{6}{8}[/latex] ÷ latex]\frac{8}{8}[/latex] = latex]\frac{6}{8[/latex] ÷ 1
latex]\frac{6}{8}[/latex]
Question 8.
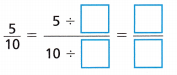
Answer:
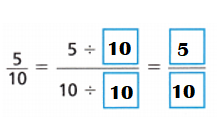
Explanation:
Equivalent fraction of \(\frac{5}{10}\):
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 5 n 10 = 10
latex]\frac{5}{10}[/latex] = latex]\frac{5}{10}[/latex] ÷ latex]\frac{10}{10}[/latex] = latex]\frac{5}{10[/latex] ÷ 1
latex]\frac{5}{10}[/latex]
Write true or false for the statement.
Question 9.
\(\frac{1}{4}\) = \(\frac{3}{7}\)
Answer:
\(\frac{1}{4}\) = \(\frac{3}{7}\) is false statement.
Explanation:
\(\frac{1}{4}\) = \(\frac{3}{7}\)
Denominator = 4 n 7.
4 × ?? = 7
=> 4 multiplied by any umber cannot be 7.
Question 10.
\(\frac{5}{6}\) = \(\frac{10}{12}\)
Answer:
\(\frac{5}{6}\) = \(\frac{10}{12}\) is true statement.
Explanation:
\(\frac{5}{6}\) = \(\frac{10}{12}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 5 n 10 = 10.
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
Question 11.
\(\frac{8}{10}\) = \(\frac{4}{5}\)
Answer:
\(\frac{8}{10}\) = \(\frac{4}{5}\) is true statement.
Explanation:
\(\frac{8}{10}\) = \(\frac{4}{5}\)
Common factor of 8 n 10 = 2.
\(\frac{8}{10}\) = \(\frac{8}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{4}{5}\)
Question 12.
Reason There is \(\frac{1}{2}\) of a vegetable pizza left. The pizza had 8 slices. How many slices of pizza are left? Show and explain how you can use equivalent fractions to solve.
Answer:
Number of slices of pizza are left = 4.
Explanation:
Quantity of a vegetable pizza left = \(\frac{1}{2}\)
Number of slices pizza had = 8.
Number of slices of pizza are left = Number of slices pizza had – \(\frac{1}{2}\)
= 8 × \(\frac{1}{2}\)
= 4.
On Your Own
Generate two equivalent fractions for the fraction.
Question 13.
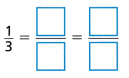
Answer:
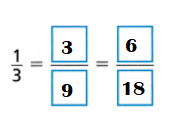
Explanation:
\(\frac{1}{3}\)
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Multiples of 1: 1,2,3,4,5,6,7,8,9,10.
Common multiple of 3 n 1 = 3,6.
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{3}{3}\) = \(\frac{3}{9}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) × \(\frac{6}{6}\) = \(\frac{6}{18}\)
Question 14.
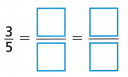
Answer:
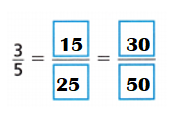
Explanation:
\(\frac{3}{5}\)
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Common multiple of 3 n 5 = 15,30.
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{5}{5}\) = \(\frac{15}{25}\)
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{10}{10}\) = \(\frac{30}{50}\)
Question 15.
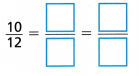
Answer:
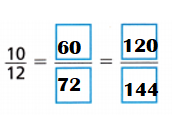
Explanation:
\(\frac{10}{12}\)
Multiples of 10: 10,20,30,40,50,60,70,80,90,100,110,120.
Multiples of 12: 12,24,36,48,60,72,84,96,108,120.
Common multiple of 10 n 12 = 60,120.
\(\frac{10}{12}\) = \(\frac{10}{12}\) ÷ \(\frac{6}{6}\) = \(\frac{60}{72}\)
\(\frac{10}{12}\) = \(\frac{10}{12}\) ÷ \(\frac{12}{12}\) = \(\frac{120}{144}\)
Question 16.
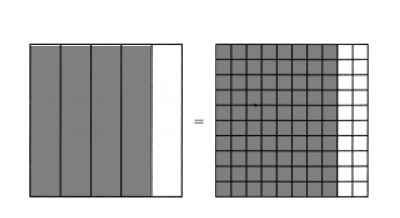
Attend to Precision Victor installs tiles on a floor. He uses blue tiles for \(\frac{4}{5}\) of the floor and white tiles for the rest. If Victor uses 100 tiles, how many of the tiles are blue?
- Explain how you can solve the problem by finding an equivalent fraction.
______________________________ - Use a visual model to represent the equivalent fractions.
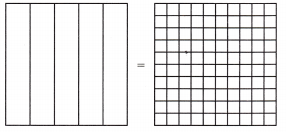
Out of 100 tiles used, _____ tiles are blue.
Answer:
Number of tiles are blue = 80.
Explanation:
Number of blue tiles Victor uses of the floor = \(\frac{4}{5}\)
Total number of tiles he uses = 100.
Number of tiles are blue = Total number of tiles he uses × Number of blue tiles Victor uses of the floor
= 100 × \(\frac{4}{5}\)
= 20 × 4
= 80.
Question 17.
Use Repeated Reasoning The table shows how much tomato juice each person drinks. Who drinks the same amount of tomato juice? Explain.
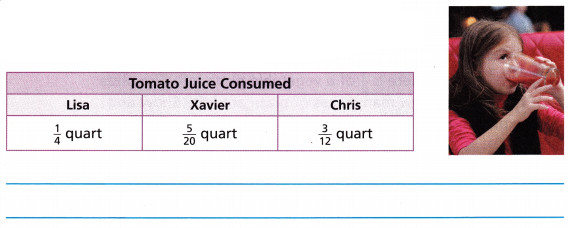
Answer:
Amount of tomato juice Lisa, Xavier and Chris drinks the same quanity of \(\frac{1}{4}\) quart.
Explanation:
Amount of tomato juice Lisa drinks = \(\frac{1}{4}\) quart.
Amount of tomato juice Xavier drinks = \(\frac{5}{20}\) quart.
Amount of tomato juice Chris drinks = \(\frac{3}{12}\) quart.
\(\frac{1}{4}\) quart.
\(\frac{5}{20}\) quart :
\(\frac{5}{20}\) ÷ \(\frac{5}{5}\) = \(\frac{1}{4}\) quart.
Common factor of 5 n 20 = 5.
\(\frac{3}{12}\) quart:
\(\frac{3}{12}\) = \(\frac{3}{12}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{4}\) quart.
Common factor of 3 n 12 = 3.