We included HMH Into Math Grade 4 Answer Key PDF Module 11 Lesson 6 Compare Fractions Using Common Numerators and Denominators to make students experts in learning maths.
HMH Into Math Grade 4 Module 11 Lesson 6 Answer Key Compare Fractions Using Common Numerators and Denominators
I Can use common numerators or denominators to compare two fractions that have different numerators and denominators.
Step It Out
1. Suki runs \(\frac{7}{12}\) mile. Lonnie runs \(\frac{3}{4}\) mile. Who runs farther?

Use a common denominator to compare the fractions.
A. Why is 12 a good choice to use as a common denominator for the two fractions?
B. Use the relationship between 12 and 4 to write \(\frac{3}{4}\) as an equivalent fraction with the common denominator 12.
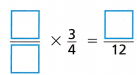
C. Compare the fractions with common denominators.
D. Use what you learned to compare the two fractions in the problem.
![]()
E. Who runs farther, Suki or Lonnie? Explain how you know.
Answer:
Lonnie runs farther than Suki because we got to know that by comparing the distance of numerator as denominator are of same values.
Explanation:
Number of miles Suki runs = \(\frac{7}{12}\).
Number of miles Lonnie runs = \(\frac{3}{4}\).
Equate denominator of \(\frac{3}{4}\) to 12:
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{9}{12}\) > \(\frac{7}{12}\)
Turn and Talk
How do common denominators help you compare two fractions?
Answer:
When you compare two fractions, it helps if they have a common denominator. Fractions with the same denominator are made up of parts of the same size. The numerators tell how many of those parts each fraction has. When two fractions have the same denominator, you can compare the numerators.
Explanation:
When you compare two fractions, it helps if they have a common denominator. The numerators tell how many of those parts each fraction has. When two fractions have the same denominator, you can compare the numerators.
Step It Out
Question 2.
Dorothy swims \(\frac{2}{5}\) kilometer. Duke swims \(\frac{3}{8}\) kilometer. Who swims farther? Use a common numerator to compare the fractions.

A. List multiples for the numerators.
Circle a common multiple.
Multiples of 2: ______
Multiples of 3: ______
B. Use the common multiple to write equivalent fractions.
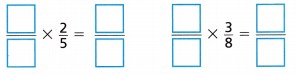
C. Compare the fractions with common numerators.
D. Use what you learned to compare the two fractions in the problem.
![]()
E. Who swims farther? Explain how you know.
_________________________
_________________________
Answer:
Dorothy swims more number of kilometers than Duke we got to know that by comparing the distance of denominator.
Explanation:
Multiples of 2: 2,4,6,8,10,12,14,16,218,20.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 2 n 3 = 6.
Number of kilometers Dorothy swims = \(\frac{2}{5}\).
Number of kilometers Duke swims = \(\frac{3}{8}\).
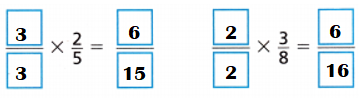
=> \(\frac{6}{15}\) > \(\frac{6}{16}\)
Check Understanding Math Board
Question 1.
Ellie ran \(\frac{5}{6}\) mile on Monday and \(\frac{7}{8}\) mile on Tuesday. Did she run farther on Monday or on Tuesday? Explain.
Answer:
She ran farther on Tuesday than Monday .
Explanation:
Number of miles Ellie ran on Monday = \(\frac{5}{6}\)
Number of miles Ellie ran on Tuesday = \(\frac{7}{8}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 7: 7,14,21,28,35,42,49,54,63,70.
Common multiple of 5 n 7 = 35.
\(\frac{5}{6}\) × \(\frac{7}{7}\) = \(\frac{35}{42}\)
\(\frac{7}{8}\) × \(\frac{5}{5}\) = \(\frac{35}{40}\)
\(\frac{35}{42}\) < \(\frac{35}{40}\)
\(\frac{5}{6}\) < \(\frac{7}{8}\)
Compare. Write >, <, or =.
Question 2.
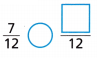
\(\frac{2}{3}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:
\(\frac{2}{3}\) < \(\frac{7}{8}\)
Explanation:
\(\frac{2}{3}\) \(\frac{7}{8}\)
Multiples of 3: 3,6,9,12,15,18,21,24,27,30
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 3 n 8 = 24.
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{8}{8}\) = \(\frac{16}{24}\)
\(\frac{7}{8}\) = \(\frac{7}{8}\) × \(\frac{3}{3}\) \(\frac{21}{24}\)
=> \(\frac{16}{24}\) < \(\frac{21}{24}\)
Question 3.
\(\frac{2}{5}\) ![]() \(\frac{4}{10}\)
\(\frac{4}{10}\)
Answer:
\(\frac{2}{5}\) = \(\frac{4}{10}\)
Explanation:
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 5 n 10 = 10.
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{2}{2}\) = \(\frac{4}{10}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\) × 1 = \(\frac{4}{10}\)
=> \(\frac{4}{10}\) = \(\frac{4}{10}\)
Question 4.
\(\frac{8}{5}\) ![]() \(\frac{3}{2}\)
\(\frac{3}{2}\)
Answer:
\(\frac{8}{5}\) > \(\frac{3}{2}\)
Explanation:
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Common multiple of 2 n 5 = 10.
\(\frac{8}{5}\) = \(\frac{8}{5}\) × \(\frac{2}{2}\) = \(\frac{16}{10}\)
\(\frac{3}{2}\) = \(\frac{3}{2}\) × \(\frac{5}{5}\) = \(\frac{15}{10}\)
=> \(\frac{16}{10}\) > \(\frac{15}{10}\)
On Your Own
Question 5.
Reason Isaiah hikes \(\frac{11}{12}\) mile along the Lake View Trail. Cheryl hikes \(\frac{3}{5}\) mile along the same trail. Who hikes farther? Use a fraction comparison strategy to support your reasoning.

_________________________
_________________________
_________________________
Answer:
Isaiah hikes farther than Isaiah because in comparison of their numerators having same denominator.
Explanation:
Number of miles Isaiah hikes along the Lake View Trail = \(\frac{11}{12}\)
Number of miles Isaiah hikes along the Lake View Trail = \(\frac{3}{5}\)
Multiples of 12: 12,24,36,48,60,72,84,96,108,120.
Multiples of 5: 5,10,15,20,25,30,35,40,45,50,55,60.
Common multiple of 12 n 5 = 60.
\(\frac{11}{12}\) = \(\frac{11}{12}\) × \(\frac{5}{5}\) = \(\frac{55}{60}\)
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{12}{12}\) = \(\frac{36}{60}\)
=> \(\frac{55}{60}\) > \(\frac{36}{60}\)
Compare. Write>, <.or =.
Question 6.
\(\frac{4}{3}\) ![]() \(\frac{5}{4}\)
\(\frac{5}{4}\)
Answer:
\(\frac{4}{3}\) > \(\frac{5}{4}\)
Explanation:
Multiples of 3: 3,6,9,12,15,18,21,24,27,30
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Common multiple of 3 n 4 = 12.
\(\frac{4}{3}\) = \(\frac{4}{3}\) × \(\frac{4}{4}\) = \(\frac{16}{12}\)
\(\frac{5}{4}\) = \(\frac{5}{4}\) × \(\frac{3}{3}\) = \(\frac{15}{12}\)
=> \(\frac{16}{12}\) > \(\frac{15}{12}\)
Question 7.
\(\frac{1}{6}\) ![]() \(\frac{2}{10}\)
\(\frac{2}{10}\)
Answer:
\(\frac{1}{6}\) < \(\frac{2}{10}\)
Explanation:
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 6 n 10 = 60.
\(\frac{1}{6}\) = \(\frac{1}{6}\) × \(\frac{10}{10}\) = \(\frac{10}{60}\)
\(\frac{2}{10}\) = \(\frac{2}{10}\) × \(\frac{6}{6}\) = \(\frac{12}{60}\)
=> \(\frac{10}{60}\) < \(\frac{12}{60}\)
Question 8.
\(\frac{9}{12}\) ![]() \(\frac{6}{8}\)
\(\frac{6}{8}\)
Answer:
\(\frac{9}{12}\) = \(\frac{6}{8}\)
Explanation:
Multiples of 12: 12,24,36,48,60,72,84,96,108,120.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 12 n 8 = 24.
\(\frac{9}{12}\) =\(\frac{9}{12}\) × \(\frac{8}{8}\) = \(\frac{72}{60}\)
\(\frac{6}{8}\) = \(\frac{6}{8}\) × \(\frac{12}{12}\) = \(\frac{72}{60}\)
=> \(\frac{72}{60}\) = \(\frac{72}{60}\)
Reason Write a numerator that makes each statement true.
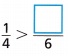
Question 9.
Answer:
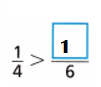
Explanation:
\(\frac{1}{4}\) \(\frac{??}{6}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 4 n 6 = 24.
\(\frac{1}{4}\) = \(\frac{1}{4}\) × \(\frac{6}{6}\) = \(\frac{6}{24}\)
\(\frac{??}{6}\) = \(\frac{??}{6}\) × \(\frac{4}{4}\) = \(\frac{4}{24}\)
Simplification:
\(\frac{6}{24}\) = \(\frac{1}{4}\) > \(\frac{4}{24}\) = \(\frac{1}{6}\)
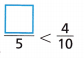
Question 10.
Answer:
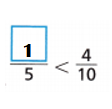
Explanation:
\(\frac{??}{5}\) \(\frac{4}{10}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 5 n 10 = 10.
\(\frac{??}{5}\) = \(\frac{??}{5}\) × \(\frac{2}{2}\) = \(\frac{2}{10}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\) × 1 = \(\frac{4}{10}\)
Simplification:
\(\frac{2}{10}\) = \(\frac{1}{5}\) < \(\frac{4}{10}\)
Question 11.
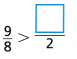
Answer:
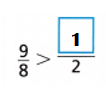
Explanation:
\(\frac{9}{8}\) \(\frac{??}{2}\)
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Common multiple of 8 n 2 = 8.
\(\frac{9}{8}\) = \(\frac{9}{8}\) × 1 = \(\frac{9}{8}\)
\(\frac{??}{2}\) = \(\frac{??}{2}\) × \(\frac{4}{4}\) = \(\frac{4}{8}\)
Simplification:
\(\frac{9}{8}\) > \(\frac{4}{8}\) = \(\frac{1}{2}\)
Question 12.
Critique Reasoning Marcos rides his bicycle \(\frac{6}{4}\) miles. Janice rides her bicycle \(\frac{14}{8}\) miles. Janice says she rides farther than Marcos because 14 > 6.
- Do you agree with Janice’s reasoning? Explain.
__________________________
__________________________
__________________________ - Use visual models to justify your answer.
Answer:
Janice says true but her reasoning is wrong because the numerators values differ not denominators.Explanation:
Number of miles Marcos rides his bicycle = \(\frac{6}{4}\)
Number of miles Janice rides her bicycle = \(\frac{14}{8}\)
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 4 n 8 = 8.
\(\frac{6}{4}\) = \(\frac{6}{4}\) × \(\frac{2}{2}\) = \(\frac{12}{8}\)
\(\frac{14}{8}\) = \(\frac{14}{8}\) × 1 = \(\frac{14}{8}\)
Simplification:
\(\frac{12}{8}\) = \(\frac{6}{4}\)< \(\frac{14}{8}\)
On Your Own
Question 13.
Open Ended Michelle has \(\frac{4}{6}\) cup of blueberries. Robin has a greater amount of blueberries, but they are measured in eighths. What could be the amount of blueberries that Robin has? Use a fraction comparison strategy to support your reasoning.

Answer:
Number of cups of blueberries Michelle has = \(\frac{1}{8}\)
Explanation:
Number of cups of blueberries Michelle has = \(\frac{4}{6}\)
Robin has a greater amount of blueberries, but they are measured in eighths.
=> Number of cups of blueberries Michelle has = \(\frac{??}{8}\)
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 6 n 8 = 24.
\(\frac{4}{6}\) = \(\frac{4}{6}\) × \(\frac{4}{4}\) = \(\frac{16}{24}\)
\(\frac{??}{8}\) = \(\frac{??}{8}\) × \(\frac{3}{3}\) = \(\frac{3}{24}\) = \(\frac{1}{8}\)
Question 14.
Use Structure Which would you use to compare \(\frac{10}{12}\) and \(\frac{2}{5}\), a common numerator or a common denominator? Explain. Use the strategy to compare the two fractions.
Answer:
\(\frac{10}{12}\) > \(\frac{2}{5}\)
Both methods are easy to solve the problem.
Explanation:
Using denominators:
compare \(\frac{10}{12}\) and \(\frac{2}{5}\)
Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 12: 12,24,36,48,60,72,84,96,108,120.
Common multiple of 5 n 12 = 60.
\(\frac{10}{12}\) = \(\frac{10}{12}\) × \(\frac{5}{5}\) = \(\frac{50}{60}\)
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{12}{12}\) = \(\frac{24}{60}\) \(\frac{50}{60}\) > \(\frac{24}{60}\)
Using Numerators:
compare \(\frac{10}{12}\) and \(\frac{2}{5}\)
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Equate numerator to 10.
\(\frac{10}{12}\)
\(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{5}{5}\) = \(\frac{10}{25}\) \(\frac{10}{12}\) > \(\frac{10}{25}\)
Compare. Write>, <,or =.
Question 15.
\(\frac{1}{8}\) ![]() \(\frac{2}{6}\)
\(\frac{2}{6}\)
Answer:
\(\frac{1}{8}\) < \(\frac{2}{6}\)
Explanation:
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Common multiple of 8 n 6 = 24.
\(\frac{1}{8}\) = \(\frac{1}{8}\) × \(\frac{3}{3}\) = \(\frac{3}{24}\)
\(\frac{2}{6}\) = \(\frac{2}{6}\) × \(\frac{4}{4}\) = \(\frac{8}{24}\) \(\frac{3}{24}\) < \(\frac{8}{24}\)
Question 16.
\(\frac{3}{8}\) ![]() \(\frac{6}{10}\)
\(\frac{6}{10}\)
Answer:
\(\frac{3}{8}\) < \(\frac{6}{10}\)
Explanation:
Multiples of 8: 8,16,24,32,40,48,56,64,72,80.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Common multiple of 8 n 10 = 40.
\(\frac{3}{8}\) = \(\frac{3}{8}\) × \(\frac{5}{5}\) = \(\frac{15}{40}\)
[\(\frac{6}{10}\) = \(\frac{6}{10}\) × \(\frac{4}{4}\) = \(\frac{24}{40}\) \(\frac{15}{40}\) < \(\frac{24}{40}\)
Question 17.
\(\frac{9}{10}\) ![]() \(\frac{11}{12}\)
\(\frac{11}{12}\)
Answer:
\(\frac{9}{10}\) < \(\frac{11}{12}\)
Explanation:
Multiples of 10: 10,20,30,40,50,60,70,80,90,100.
Multiples of 12: 12,24,36,48,60,72,84,96,108,120.
Common multiple of 10 n 12 = 60.
\(\frac{9}{10}\) = \(\frac{9}{10}\) × \(\frac{6}{6}\) = \(\frac{54}{60}\)
\(\frac{11}{12}\) = \(\frac{11}{12}\) × \(\frac{5{5}\) = \(\frac{55}{60}\) \(\frac{54}{60}\) < \(\frac{55}{60}\)
Question 18.
Reason Sasha and Elliot are picking strawberries.
Sasha picks \(\frac{7}{5}\) pounds of strawberries. Elliot picks \(\frac{8}{6}\) pounds of strawberries. Who picks more strawberries?
- Write the fractions as mixed numbers.
_________________________ - Explain how you can use the mixed numbers to compare the fractions and solve the problem.
_________________________
_________________________
_________________________
_________________________
Answer:
Sasha picks more strawberries than Elliot because numerators are same and denominator comparison, Sasha is more.Explanation:
Number of pounds of strawberries Sasha picks = \(\frac{7}{5}\)
Number of pounds of strawberries Elliot picks = \(\frac{8}{6}\)
Mixed fraction of number of pounds of strawberries Sasha picks = \(\frac{7}{5}\)
=> 1 + \(\frac{2}{5}\) = 1\(\frac{2}{5}\)
Mixed fraction of number of pounds of strawberries Elliot picks = \(\frac{8}{6}\)
=> 1 + \(\frac{2}{6}\) = 1\(\frac{2}{6}\)Multiples of 5: 5,10,15,20,25,30,35,40,45,50.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 5 n 6 = 30.
\(\frac{7}{5}\) = \(\frac{7}{5}\) × \(\frac{6}{6}\) = \(\frac{42}{30}\)
\(\frac{8}{6}\) = \(\frac{8}{6}\) × \(\frac{5{5}\) = \(\frac{40}{30}\) \(\frac{42}{30}\) > \(\frac{40}{30}\)