We included HMH Into Math Grade 4 Answer Key PDF Module 11 Lesson 3 Explain Fraction Equivalence Using Visual Models to make students experts in learning maths.
HMH Into Math Grade 4 Module 11 Lesson 3 Answer Key Explain Fraction Equivalence Using Visual Models
I Can use a visual model to show that two fractions are equivalent and explain why they are equivalent.
Spark Your Learning
Compare Jason’s and Kym’s turns. Whose turn is closer to being a full turn? Use the visual model of each turn to explain.
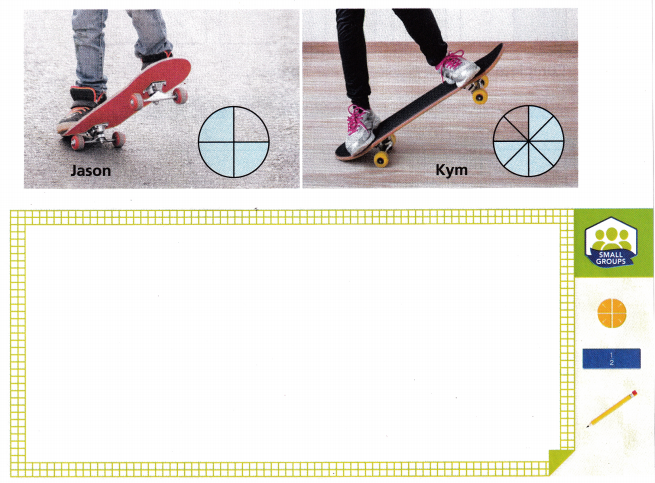
Answer:
Both are close to turn closer to being a full turn because both turns are same.
Explanation:
Jason’s turns:
Number of shaded turns of Jason = 3.
Total number of turns of Jason = 4.
Number of turns Jason makes = Number of shaded turns of Jason ÷ Total number of turns of Jason
= 3 ÷ 4 or \(\frac{3}{4}\)
Kym’s turns:
Number of shaded turns of Kym = 6.
Total number of turns of Kym = 8.
Number of turns Kym makes = Number of shaded turns of Kym ÷ Total number of turns of Kym
= 6 ÷ 8 or \(\frac{6}{8}\)
= \(\frac{6}{8}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{4}\)
Turn and Talk How do the number and size of parts compare in the visual models for Jason’s and Kym’s turns?
Answer:
Total number of turns(size of parts) and number of turns they made (shaded part) are compare in the visual models for Jason’s and Kym’s turns
Explanation:
Number of shaded turns of Jason = 3.
Total number of turns of Jason = 4.
Number of turns Jason makes = \(\frac{3}{4}\)
Number of shaded turns of Kym = 6.
Total number of turns of Kym = 8.
Number of turns Kym makes = \(\frac{6}{8}\)
Build Understanding
1. Sam wants to paint a skateboard ramp with a cool design. He has just enough paint to cover half of the ramp. Show different designs Sam can use. Divide the last two rectangles into a different number of equal parts. Shade each of the last three rectangles to show \(\frac{1}{2}\).

Complete the table to record your findings.
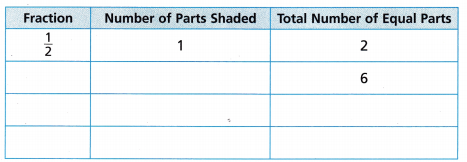
Look at the first fraction you wrote in the table.
A. How does the size of the parts compare to those in \(\frac{1}{2}\)?
____________________________
B. How does the number of parts and the number of shaded parts compare to those in \(\frac{1}{2}\) ?
____________________________
Answer:
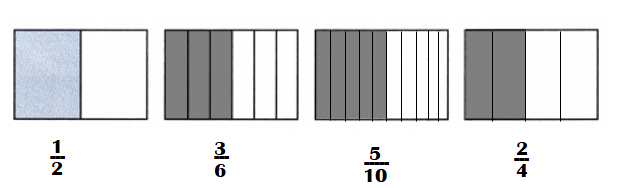
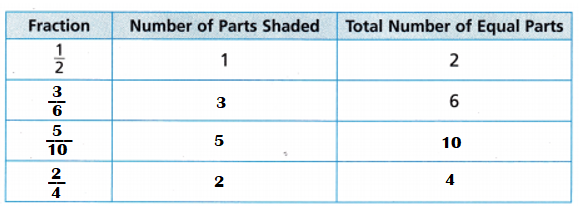
Explanation:
\(\frac{1}{2}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{3}{3}\) = \(\frac{3}{6}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{5}{5}\) = \(\frac{5}{10}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{2}{2}\) = \(\frac{2}{4 }\)
Turn and Talk Look for patterns in your table. How does the numerator and denominator for each fraction compare to those in \(\frac{1}{2}\) ?
Answer:
\(\frac{1}{2}\) < \(\frac{7}{2}\).
Explanation:
Fraction is a number that represents a portion of a whole number. Some fractions are larger than others.
Fraction = Numerator by Denominator.
Given Fraction = \(\frac{1}{2}\)
For example:
Which is bigger \(\frac{1}{2}\) and \(\frac{7}{2}\)
\(\frac{1}{2}\) < \(\frac{7}{2}\) because we check denominators and numerators.
If denominators are same , the value high in numerator is big.
If Numerators are same , the value small in denominators is big.
Step It Out
Connect to Vocabulary
Two or more fractions that name the same amount are called equivalent fractions.
2. Write an equivalent fraction for \(\frac{1}{2}\).
A. Compare the rectangle with 2 parts that shows \(\frac{1}{2}\) in Task 1 to the rectangle with 6 parts you shaded to show \(\frac{1}{2}\). Complete the equation.

B. How can you use multiplication to describe the relationship between the numerators? Between the denominators?
C. Complete the equation to show how to write a fraction equivalent to \(\frac{1}{2}\).
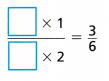
D. Complete the statement about any fraction.
To write an equivalent fraction, multiply the numerator and ____ of the fraction by ____
Answer:
Equivalent fraction for \(\frac{1}{2}\) = \(\frac{3}{6}\)
Explanation:
Equivalent fraction for \(\frac{1}{2}\):
\(\frac{3}{3}\) × \(\frac{1}{2}\) = \(\frac{3}{6}\)
Turn and Talk Look at the other fractions you wrote in Task 1. Do they agree with the statement in Part D? Explain.
Answer:
Yes, they agree with the statement in Part D. \(\frac{1}{2}\) = \(\frac{3}{6}\) both are same
Explanation:
Task 1: Fraction \(\frac{1}{2}\)
Part D: Fraction \(\frac{3}{6}\)
Check Understanding Math Board
Question 1.
Jason makes a \(\frac{5}{6}\) turn on his skateboard. Samantha makes a \(\frac{10}{12}\) turn. Did they make the same-sized turn? Use the visual models to explain.
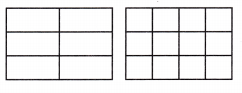
Answer:
They make the same-sized turn.
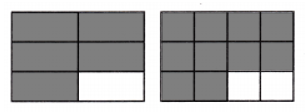
Explanation:
Number of turns on his skateboard Jason makes = \(\frac{5}{6}\)
Number of turns on his skateboard Samantha makes = \(\frac{10}{12}\)
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
\(\frac{10}{12}\) = \(\frac{10}{12}\) ÷ \(\frac{2}{2}\) = \(\frac{10}{12}\)
On Your Own
Question 2.
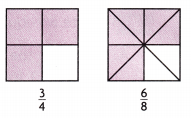
Are the fractions \(\frac{3}{4}\) and \(\frac{6}{8}\) equivalent? Use the visual models to explain how you know.
Answer:
Yes, they are the fractions \(\frac{3}{4}\) and \(\frac{6}{8}\) equivalent
Explanation:
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{2}{2}\) = \(\frac{6}{8}\) .
\(\frac{6}{8}\) = \(\frac{6}{8}\) ÷ \(\frac{2}{2}\) = \(\frac{3}{4}\)
Model with Mathematics Complete the equation to show how the two fractions are equivalent.
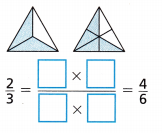
Question 3.
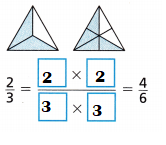
Answer:
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{2}{2}\) = \(\frac{4}{6}\)
\(\frac{4}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
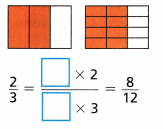
Question 4.
Answer:
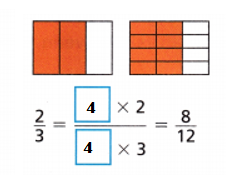
Explanation:
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
\(\frac{8}{12}\) = \(\frac{8}{12}\) ÷ \(\frac{4}{4}\) = \(\frac{2}{3}\)
Question 5.
Reason A recipe asks for \(\frac{1}{4}\) teaspoon of salt. Jonas only has a \(\frac{1}{8}\)—teaspoon measuring spoon. He fills that spoon two times to get \(\frac{1}{4}\) teaspoon of salt. Use visual models to explain why this works.

Answer:
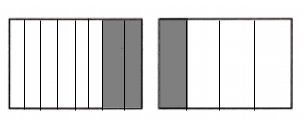
Explanation:
Quantity of teaspoon of salt a recipe asks =\(\frac{1}{4}\)
Quantity of teaspoon measuring spoon Jonas has = \(\frac{1}{8}\)
\(\frac{1}{8}\) = \(\frac{1}{8}\) × 2 = \(\frac{2}{8}\) = \(\frac{1}{4}\)
I’m in a Learning Mindset!
Did the practice help me master how to use visual models to explain equivalent fractions? Why or why not?
____________________________________
Answer:
Yes, this practice has helped the master to use visual models to explain equivalent fractions because its easy to understand the figures.
Explanation:
Visual models makes headway in identifying as well as representing equivalent fractions easily.