An Identity Matrix or Unit matrix is a matrix that is an n × n square matrix that consists of all the diagonal elements as one and all other elements as zero. It is also called an Elementary matrix. The unit matrix is represented by I or In where n is the size of the square matrix.
The identity matrix is used as the multiplicative identity of square matrices in the entire matrices concepts. If any square matrix is multiplied by the identity matrix or Unit matrix, the resultant will be the square matrix. Generally, we use Identity Matrix to find the inverse of a matrix. The 10th Grade Math Unit Matrix concept is explained clearly in this article.
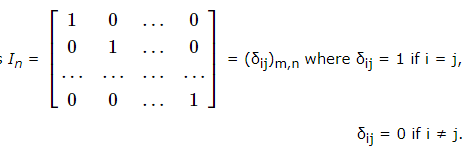
Also, find
Identity Matrix Definition | What is a Unit Matrix?
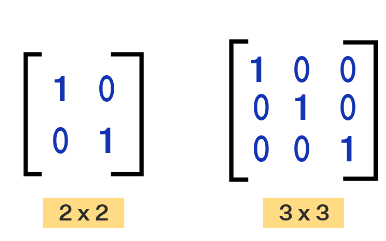
The Identity Matrix is a Square Matrix that consists of the main diagonal with 1 digit and all other elements with zero. The degree of a unit matrix is n × n. We use the notation to represent an identity matrix as I or In. The elements present in the given unit matrix remain unchanged. See the below examples to find the 2 × 2 and 3 × 3 identity matrices.
Identity Matrix is donated by In × n, where n × n represents the order of the matrix.
A × I n × n = A, A = any square matrix of order n × n.
Identity Matrix Properties
Different Properties of the Identity matrix are given here with examples. Read all the properties to know more about the elementary matrix.
1. Identity matrix is always a Square Matrix
The unit Matrices are always square matrices as they have an equal number of rows and columns. For any whole number n, there’s a related Identity matrix, n × n.
2. Multiplication of any matrix by the unit matrix, gives the matrix itself.
If any matrix is multiplied by the unit matrix, then the result will become the same matrix. For “a × b” matrix M, we get IaM = M = MIb. If B is considered to be a square matrix of order m and I is considered to be an identity matrix of order m, then BI = IB = B. The identity functions like if you multiply a matrix by the unit matrix of the same order, then you get the same initial matrix.
Example: \( A =\left[
\begin{matrix}
5&10&15 \cr
20&25&30 \cr
\end{matrix}
\right]
\) and \( I =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\), then find AI?
Solution:
Given matrices are \( A =\left[
\begin{matrix}
5&10&15 \cr
20&25&30 \cr
\end{matrix}
\right]
\) and \( I =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\).
A is a 2 × 3 matrix and I is a 2 × 2 matrix.
Multiply A with I. AI = \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) \( \left[
\begin{matrix}
5&10&15 \cr
20&25&30 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
5 + 0&10 + 0&15 + 0 \cr
0 + 20&0 + 25&0 + 30 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
5&10&15 \cr
20&25&30 \cr
\end{matrix}
\right]
\)
Therefore, the Multiplication of any matrix by the unit matrix gives the matrix itself
3. If [a] is a scalar matrix then [a] = aI.
Example: [a] = [2], I = \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
Then, 2I = 2 \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
2&0 \cr
0&2 \cr
\end{matrix}
\right]
\) = [2].
4. When we multiply one unit matrix of order n by another unit matrix of the same order, then the output matrix will also be a unit matrix of order n.
Example: Let I = \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
Multiply I with I matrix.
\( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) × \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
5. We will always get an identity matrix after multiplying two inverse matrices.
6. The determinant of an identity matrix is always equal to 1. det|I| = 1.
Read More:
Identity Matrix Examples
Various problems given here will let you know the unit matrix operations and properties clearly. So, solve every problem and understand the concept deeply.
Example 1: Determine if the given matrix is a unit matrix.
\(A = \left[
\begin{matrix}
1&1 \cr
2&1 \cr
\end{matrix}
\right]
\)
Solution: The given matrix is \(A = \left[
\begin{matrix}
1&1 \cr
2&1 \cr
\end{matrix}
\right]
\)
The Identity Matrix consists of all the diagonal elements as 1 and other elements as zero. In the given matrix A, all the diagonal matrices are 1 but the remaining elements are not zero.
Therefore, the given matrix \(A = \left[
\begin{matrix}
1&1 \cr
2&1 \cr
\end{matrix}
\right]
\) is not an identity matrix.
Example 2: If \(A = \left[
\begin{matrix}
a -4 &0 \cr
0&b – 5 \cr
\end{matrix}
\right]
\) is a unit matrix, then find the values of a and b.
Solution: Given matrix is \(A = \left[
\begin{matrix}
a -4 &0 \cr
0&b – 5 \cr
\end{matrix}
\right]
\) which is equal to \(A = \left[
\begin{matrix}
1 &0 \cr
0&1 \cr
\end{matrix}
\right]
\)
Comparing the elements of the matrices.
a – 4 = 1; a = 1 + 4; a = 5.
b – 5 = 1; b = 5 + 1; b = 6.
Therefore, the values of a and b are 5 and 6.
Example 3: Write an example of a 3 × 3 order unit matrix.
Solution: The unit matrix is the one having ones on the main diagonal & other entries as ‘zeros’. Also, for 3 × 3 order unit matrix, it consists of 3 rows and 3 columns.
Therefore, the 3 × 3 order unit matrix is \( \left[
\begin{matrix}
1&0&0 \cr
0&1&0\cr
0&0&1\cr
\end{matrix}
\right]
\)
Example 4. What is the determinant of a unit matrix?
Solution: The determinant of a unit matrix is 1.
FAQs on Identity Matrix
Faqs on Unit Matrix are given below with an explanation. Read all the faqs and score better in the exam.
1. What is an Identity Matrix?
An identity matrix is a unit matrix of order n x n where each main diagonal element is equal to 1, and the remaining elements of the matrix are equal to 0. The unit matrix is denoted by I or In.
2. Is the identity matrix nonsingular?
Yes, the identity matrix is said to be nonsingular. It is because a unit matrix determinant is not equal to 0. Also, it is the only idempotent matrix with a non-zero determinant.
3. Is Unit Matrix a Scalar Matrix?
Yes, a unit matrix is a scalar matrix when the diagonal elements are equal to 1 and the remaining elements are 0. A scalar matrix becomes a unit matrix when a scalar quantity 1 is multiplied by a unit matrix.
4. How Do You Represent the Unit Matrix?
An Identity matrix can be represented by I where all the diagonal elements are equal to 1 and the remaining elements are equal to 0.
5. Given an example of a unit matrix.
\(A = \left[
\begin{matrix}
1 &0 \cr
0&1 \cr
\end{matrix}
\right]
\) is the example of a unit matrix. It is a 2 × 2 unit matrix.
Conclusion
Check out whether the unit matrix is the same as the identity matrix by reading this article. We have given a clear explanation regarding the identity matrix with examples and faqs. Different Properties of the Unit Matrix are also included in this article for a better understanding of the identity matrix. Read the complete article and prepare well for the exam.
