Equal Matrices are the matrices that have the same number of rows, same number of columns, and also the same elements. If the order of the matrices is not equal and the elements present in the matrix are not equal, then those matrices are said to be unequal.
Let us discuss deeply the definition of equality of matrices and also the conditions that are required for matrix equality. Also, different examples are given to prove the equality of matrices in this article. Our 10th Grade Math equality matrix article will help you to identify the matrices they are with equal order and equal elements.
Read More About,
Equal Matrices Definition
Equality of Matrices is defined by comparing two matrices having the same order and same elements. If we take two matrices, their dimensions must match with each other, and also their elements also must match with each other. Also, the equal matrices have the same number of rows and a same number of columns.
Example: Two matrices A = [aij] and B = [bij] are said to be equal if and only if A and B have the same order. The matrices A and B have the same number of columns and the same number of rows. Also, corresponding elements of A and B must equal, i.e., aij = bij for all i and j where i = 1, 2, 3, ….., m; j = 1, 2, 3, ……., n. This is the exact definition of the Equal Matrix.
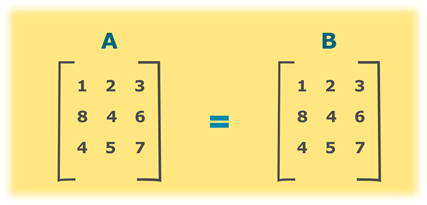
Conditions for Equality Matrix
Below are different conditions need for the equality matrices to be true. The main conditions for the equality of matrices are
If A = [aij]m×n and B = [bij]p×q
- Both matrices A and B must have the same number of rows. m must be equal to p.
- Matrices A and B must have the same number of columns. n must be equal to q.
- The elements of matrices A and B need to be equal. aij = bij for all i and j.
Example: \( A =\left[
\begin{matrix}
3&1 \cr
\end{matrix}
\right]
\) \( B =\left[
\begin{matrix}
3&1 \cr
\end{matrix}
\right]
\) are two equal matrices.
They both are 1×2 matrices. Also, the elements of the two matrices are the same.
Therefore, two matrices are equal matrices.
Also, read
Equality of Matrices Examples | Solving Equal Matrices Questions
See different examples given below to find which matrices are equal and which are not equal. Also, the rules for equality matrices and tricks to know equal matrices are given in the problems.
Example 1.
Check if the matrices \( A =\left[
\begin{matrix}
2&4&6 \cr
8&10&12 \cr
14&16&18 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
1&3&5 \cr
7&9&11 \cr
13&15&17 \cr
\end{matrix}
\right]
\) are equal or not using equality of matrices definition.
Solution:
Given matrices are \( A =\left[
\begin{matrix}
2&4&6 \cr
8&10&12 \cr
14&16&18 \cr
\end{matrix}
\right]
\) and \( B =\left[
\begin{matrix}
1&3&5 \cr
7&9&11 \cr
13&15&17 \cr
\end{matrix}
\right]
\)
The order of the two matrices is equal i.e, 3 × 3. The same number of rows and columns. So, the first condition for matrix equality is satisfied.
Now, check the elements present in the given matrices. (1, 1)th element = 2 and 1, (1, 2)th element = 4 and 3.
The elements present in the two matrices are not equal.
Therefore, the given matrices are not equal.
Example 2.
Two matrices A = [a+b 4 5 2x 3b] and B = [4 4 5 16 15] are equal. Find the values of a, b , x.
Solution:
Given matrices are A = [a+b 4 5 2x 3b] and B = [4 4 5 16 15] are equal.
The elements of the given matrices are equal.
a + b = 4
2x = 16; x = 16/2 = 8.
3b = 15; b = 15/3 = 5.
a + b = 4; a + 5 = 4; a = 4 – 5 = -1; a = -1.
Hence, a = -1, b = 5, x = 8.
Example 3.
Write othe matrix that is equal to \( A =\left[
\begin{matrix}
2&3&7 \cr
11&15&10 \cr
\end{matrix}
\right]
\)
Solution:
Given matrix is \( A =\left[
\begin{matrix}
2&3&7 \cr
11&15&10 \cr
\end{matrix}
\right]
\)
To show the equal matrix of the given matrix the number of rows and number of columns of the given matrix needs to be equal to the required matrix. Also, elements of the matrices are also equal for the required matrix.
Therefore, the required matrix is \( A =\left[
\begin{matrix}
2&3&7 \cr
11&15&10 \cr
\end{matrix}
\right]
\)
FAQs on Equality of Matrices PDF
Check different frequently asked questions and answers on matrices equality here. We have included regularly asked questions and answers below.
1. What is Equality of Matrices in Math?
Two or more matrices are said to be Equal matrices if they have the same dimensions and all corresponding elements of the matrices are equal.
2. What are the Rules for Equality of Matrices?
Below are the three rules need for matrix equality. If A = [aij]m×n and B = [bij]p×q :
- A and B Matrices have the same number of rows, i.e., m = p
- A and B Matrices have the same number of columns, i.e., n = q
- Corresponding elements of A and B are equal, i.e., aij = bij for all i and j.
3. How to Solve Equality of Matrices?
Compare the elements and order of the equal matrices to solve them. As the elements of equal matrices are equal, the unknown element given on one matrix is equal to the elements present in the other matrix.
4. Given one Example of an Equal Matrix.
\( A =\left[
\begin{matrix}
2&3&7 \cr
11&15&10 \cr
\end{matrix}
\right]
\) = \( B =\left[
\begin{matrix}
2&3&7 \cr
11&15&10 \cr
\end{matrix}
\right]
\) is the example of equal matrix.
Summary
The equal matrix concept is included here with a definition, rules, and examples. Learn the entire article without missing any part of the article to get a grip on the equal matrices concept. Different examples will help you to know which is an equal matrix and which is not.
