A column matrix is a matrix that consists of only one column. The representation of the order of the column matrix is by m x 1. In a column matrix, the rows will have single elements. Row and column in a matrix will have the elements. The column elements are vertically arranged and the row elements are horizontally arranged.
A row matrix will have a single wor and a column matrix will have a single column only. Complete matrix concepts ate given in the 10th Grade Math articles. Read the complete articles and learn the matrix concepts.
Also, check
Column Matrix Definition | What is Column Matrix?
A column matrix is a type of matrix that has only one single column. A column matric consists of only one column and multiple wors. If we consider the m × n matrix where m is the number of rows and n is the number of columns, then in a column matrix, n = 1. So, the vertical lines of elements form a column matrix.
The column matric consists of a rectangular array of elements arranged vertically.
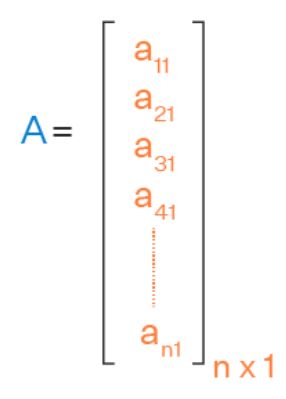
Examples of Column Matrix
Check out the below examples to know the column matrices.
\( A =\left[
\begin{matrix}
1 \cr
18 \cr
\end{matrix}
\right]
\)
The order of the above matrix is 2 × 1.
\( B =\left[
\begin{matrix}
3 \cr
5 \cr
11 \cr
13 \cr
\end{matrix}
\right]
\)
The order of the above matrix is 4 × 1.
\( C =\left[
\begin{matrix}
2 \cr
4 \cr
6 \cr
\end{matrix}
\right]
\)
The order of the above matrix is 3 × 1.
Properties of Column Matrix
Below are the different properties of the column matrix.
- The column matrix will have only one column.
- Also, a column matrix will have numerous rows.
- The column matrix is also called the rectangular matrix.
- A column matrix will be multiplied only by a row matrix.
- The number of elements present in a column matrix is equal to the number of rows present in the matrix.
- The transpose of a column matrix is a row matrix.
- We can add or subtract the column matrix with other column matrices having the same order.
- The multiplication of a column matrix with a row matrix gives a singleton matrix.
Refer More:
Operations On Column Matrix
We can perform addition, subtraction, multiplication, and also division on column matrices by following some rules.
- We can add the column matrices with the other column matrices that have the same order.
- The multiplication of a column matrix will happen only with the row matrix.
- The number of columns in the column matrix for multiplication must be equal to the number of rows in the row column.
Column Matrix Examples
We have given different examples below on the rectangular matrix or column matrix. Understand how we perform different operations on the Column Matrix by solving every problem given below.
Example 1.
Find the transpose of a column matrix
\( A =\left[
\begin{matrix}
3 \cr
17 \cr
\end{matrix}
\right]
\)
Solution:
The given matrix is \( A =\left[
\begin{matrix}
3 \cr
17 \cr
\end{matrix}
\right]
\)
To find the transpose of the given column matrix, the elements of the column matrix must be written as row elements.
\( A =\left[
\begin{matrix}
3&17 \cr
\end{matrix}
\right]
\)
Therefore, the transpose of given column matrix is \( A =\left[
\begin{matrix}
3&17 \cr
\end{matrix}
\right]
\).
Example 2.
Give the examples of column matrix of the orders of
a. 2 x 1
b. 3 x 1
c. 4 x 1
d. 5 x 1
e. 6 x 1
Solution:
a. Given that the matrix is 2 x 1.
The example of a column matrix of the order 2 x 1 is \( A =\left[
\begin{matrix}
3 \cr
17 \cr
\end{matrix}
\right]
\)
b. Given that the matrix is 3 x 1.
The example of a column matrix of the order 3 x 1 is \( A =\left[
\begin{matrix}
1 \cr
3 \cr
5 \cr
\end{matrix}
\right]
\)
c. Given that the matrix is 4 x 1.
The example of a column matrix of the order 4 x 1 is \( A =\left[
\begin{matrix}
1 \cr
3 \cr
5 \cr
7 \cr
\end{matrix}
\right]
\)
d. Given that the matrix is 5 x 1.
The example of a column matrix of the order 5 x 1 is \( A =\left[
\begin{matrix}
1 \cr
3 \cr
5 \cr
7 \cr
9 \cr
\end{matrix}
\right]
\)
e. Given that the matrix is 6 x 1.
The example of a column matrix of the order 6 x 1 is \( A =\left[
\begin{matrix}
1 \cr
3 \cr
5 \cr
7 \cr
9 \cr
11 \cr
\end{matrix}
\right]
\)
Example 3.
What is the order of the given column matrix \( A =\left[
\begin{matrix}
1 \cr
5 \cr
9 \cr
11 \cr
\end{matrix}
\right]
\)
Solution:
Given matrix is \( A =\left[
\begin{matrix}
1 \cr
5 \cr
9 \cr
11 \cr
\end{matrix}
\right]
\)
It consists of 4 rows and 1 column.
Therefore, it is a 4 x 1 matrix.
Example 4.
Which of the following is the order of a column matrix?
a. 4 x 1
b. 1 x 2
c. 2 x 3
d. 3 x 2
Solution:
We know that the order of the column matrix is m x 1. Therefore, from the given options 4 x 1 is the column matrix.
Therefore, the answer is a. 4 x 1
FAQs on Column Matrix
1. What is a column matrix?
A matrix is called a column matrix when it has only one column.
2. What is the order of the column matrix?
The order of the column matrix is n x 1, where n is the number of rows.
3. What is the Transpose of a Column Matrix?
The transpose of a column matrix gives a row matrix. If n x 1 is the Column Matrix, then the transpose of it is 1 x n which is a row matrix. The column matrix elements are arranged in a vertical manner and the row matrix elements are arranged in a horizontal format.
4. Give an example of a column matrix with the order 1 x 1.
[7] is an example of a column matrix with order 1 x 1.
Conclusion
Column Matrix or rectangular matrix definition, examples, and explanation are included in this article. Know what is the order of the column matrix and operations performed on the column matrix by reading the entire article. We have given different tricks and problems to help the students to get good marks in the exam. Also, the properties of the column matrix will give you the clarity on which operations need to perform on column matrices.
