Are you confused about learning Fractions? Learn Fractions free of cost using this website. It also explains the definition of fractions, Fraction Notation, Types of Fractions. You can also see the examples of Fractions for a better understanding of the concept.
Do Check:
Fraction – Definition
A fraction represents the part of the collection or a whole. When we divide a collection or whole into equal parts each part is a fraction of the whole.
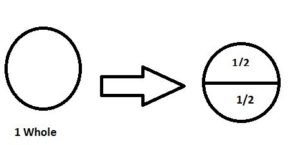
In the above diagram, the circle is divided into two equal parts. Each part is one half.
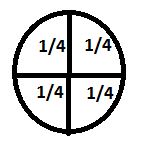
In the above diagram, the circle is divided into 4 equal parts. Each part is one-fourth. Fraction also represents the collection.

Here, the collection of plates are 8.
One-half of the 8 plates = 4
Thus,\(\frac {1}{ 2 } \) =\(\frac { 4 }{ 8 } \)
For example, In a group of 10 Lecturers, 4 are gents and 6 are ladies. Find the fraction of Lady lecturers and gents lecturers?
The fraction of Lady Lecturers is \(\frac { 6 }{ 10 } \)
The fraction of Gents Lecturer is \(\frac { 4 }{ 10 } \)
Fraction Notation
A fraction has two parts. The two parts are separated by a solidus or a vinculum. The number on the top of the solidus is called the numerator. It tells how many no. of equal parts of the whole or collection is taken. The number below the solidus is called the denominator. It shows all the divisible number of equal parts the whole or the total number of equal parts which are there in a collection.
Example:
In \(\frac { 4 }{ 8 } \) 4 represents the Numerator, which tells the no of equal parts taken. 8 represents the Denominator, which tells the total no of equal parts in a whole or collection. Examples of fractions are \(\frac { 3 }{ 8 } \), \(\frac { 2 }{ 6 } \), \(\frac { 6 }{ 8 } \) e.t.c.
Fractions are mainly divided into three types. They are 1. Proper Fraction 2. improper fraction 3. Mixed Fraction
Proper Fraction:
If the numerator is smaller than the denominator then It is called the Proper Fraction. For example \(\frac { 2 }{ 4 } \), \(\frac { 4 }{ 7 } \), \(\frac { 3 }{ 8 } \)e.t.c.
Improper Fraction:
If the numerator is larger than or equal to the denominator then it is called Improper Fraction. For example \(\frac { 5 }{ 2 } \) ,\(\frac { 4 }{ 3} \), \(\frac { 13 }{ 2 } \),etc.
Mixed Fraction:
A whole number and proper fraction together are called a Mixed Fraction. For example \(\frac { 2 1 }{ 5} \),\(\frac { 6 2 }{ 7 } \),etc.
Examples of Fraction
Example 1:
If we have two pomegranates in a basket of 7 fruits. How many fruits are there in the basket? How many pomegranates are there in the basket?

Solution:
There are seven fruits in the basket. We have two pomegranates in the basket of 7 fruits. i.e. we can write as \(\frac { 2 }{ 7 } \).
Example 2:
In the below figure the square is divided into six equal parts. Find the fractions of the shaded part and unshaded part of the square?

Solution:
In the above figure, the square is divided into six equal parts.
Four parts are shaded. The shaded part represents the four-sixth of the strip. we can write it as\(\frac { 4 }{ 6 } \).
The number of unshaded parts is two. The unshaded part represents two-sixth of the strip. It can be written as\(\frac { 2 }{6} \).
In the fraction \(\frac { 4 }{ 6 } \),4 represents the shaded part and six represent the total number of parts.
In the fraction \(\frac { 2 }{ 6 } \),2 represents the unshaded part and six represent the total number of parts.
Example 3:
In the below figure the circle is divided into four equal parts. Find the shaded part and unshaded part of the circle?
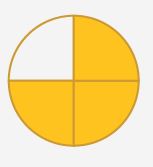
Solution:
In the above figure, the circle is divided into 4 equal parts. In the circle three parts are shaded and one part is not shaded. The shaded part represents the three-fourth of the circle. It can be written as\(\frac { 3 }{ 4} \). The unshaded part represents one-fourth of the circle. It can be written as \(\frac { 1 }{ 4 } \).
Example 4:
In a hospital, 6 children are born on the same day. out of six, two are boys and four are girls. Find the fraction of girls and boys?
Solution:
No.of children born in the hospital=6
Fraction of girls= \(\frac { 4 }{ 6 } \).
Fraction of boys= \(\frac { 2 }{ 6} \).
Example 5:
Gopal bought a basket of 20 fruits that contains 10 bananas, 5 apples,5 mangoes. Find the fractions of bananas, mangoes, apples?
Solution:
No of fruits in the basket=20
The fraction of bananas in the basket= \(\frac { 10 }{ 20 } \)
The fraction of apples in the basket=\(\frac { 5 }{ 20 } \)
The fraction of mangoes in the basket=\(\frac { 5 }{ 20 } \)
FAQs on Fraction as Part of Collection
1. What is Fraction?
A fraction represents the part of the collection or whole.
2. What are the types of fractions?
They are three types of fractions.1. Proper fractions 2. improper fractions 3. Mixed fractions.
3. What does the upper part of the fraction represent?
The upper part of the fraction represents the Numerator.
4. What does the Lower part of the fraction represent?
The Lower part of the fraction represents the Denominator.
5. What is a Proper Fraction and give the examples?
If the numerator is smaller than the denominator then It is called the Proper Fraction. It is called Proper Fraction.For example [atex]\frac { 1 }{ 4 } [/latex], \(\frac { 5}{ 7 } \), \(\frac { 2 }{ 9 } \),etc.
