Everyday Mathematics 5th Grade Answer Key Unit 5 Operations with Fractions
Everyday Mathematics Grade 5 Home Link 5.1 Answers
Using Equivalent Fractions to Solve Problems
Question 1.
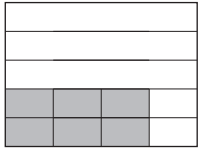
Fill in the equivalent fractions in the table below.
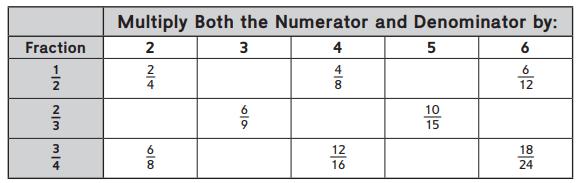
Answer:
Estimation:
Filled in the equivalent fractions in the table above as
\(\frac{1}{2}\) X 2 = \(\frac{3}{6}\),
\(\frac{1}{2}\) X 5 = \(\frac{5}{10}\),
\(\frac{2}{3}\) X 2 = \(\frac{4}{6}\),
\(\frac{2}{3}\) X 4 = \(\frac{8}{12}\),
\(\frac{2}{3}\) X 6 = \(\frac{12}{18}\),
\(\frac{3}{4}\) X 3 = \(\frac{9}{12}\),
\(\frac{3}{4}\) X 5 = \(\frac{15}{20}\).
Estimate. Then solve by finding fractions with a common denominator. Write a number sentence to show which fractions you used.
Example: \(\frac{1}{3}\) + \(\frac{7}{12}\) = ?
Estimate: close to 1, because \(\frac{1}{3}\) is less than \(\frac{1}{2}\), and \(\frac{7}{12}\) is a little more than \(\frac{1}{2}\).
Common denominator: 12
Number sentence: \(\frac{4}{12}\) + \(\frac{7}{12}\) = ?
Answer:
\(\frac{11}{12}\),
Explanation:
Given to find \(\frac{1}{3}\) + \(\frac{7}{12}\) = ,
As both denominators are different first we need to
make common denominators means we need to multiply
numerator and denominator by 4 as
\(\frac{1}{3}\) X 4 = \(\frac{1 X 4}{3 X 4}\) =
\(\frac{4}{12}\) now we add as
\(\frac{4}{12}\) + \(\frac{7}{12}\) as
denominators are common as 12 we add numerators as
\(\frac{4 + 7}{12}\) = \(\frac{11}{12}\),
therefore common denominator is 12 and
Number sentence: \(\frac{4}{12}\) + \(\frac{7}{12}\) =
\(\frac{11}{12}\).
Question 2.
\(\frac{6}{8}\) – \(\frac{1}{2}\) = ?
Common denominator: _____8_____
Number sentence: _____\(\frac{6}{8}\) – \(\frac{1}{2}\) = \(\frac{2}{8}\),
Answer:
Common denominator: 8,
Number sentence: \(\frac{6}{8}\) – \(\frac{1}{2}\) = \(\frac{2}{8}\),
Explanation:
Given to find \(\frac{6}{8}\) – \(\frac{1}{2}\) = ,
As both denominators are different first we need to
make common denominators means we need to multiply
numerator and denominator by 4 as
\(\frac{1}{2}\) X 4 = \(\frac{1 X 4}{2 X 4}\) =
\(\frac{4}{8}\) now we subtract as
\(\frac{6}{8}\) – \(\frac{4}{8}\) as
denominators are common as 8 we subtract numerators as
\(\frac{6 – 4}{8}\) = \(\frac{2}{8}\),
therefore common denominator is 8 and
Number sentence: \(\frac{6}{8}\) – \(\frac{4}{8}\) =
\(\frac{2}{8}\).
Question 3.
\(\frac{1}{6}\) + \(\frac{2}{3}\) = ?
Common denominator: ____6______
Number sentence: ____\(\frac{1}{6}\) + \(\frac{2}{3}\) = \(\frac{5}{6}\)_____
Answer:
Common denominator: 6
Number sentence: \(\frac{1}{6}\) + \(\frac{2}{3}\) = \(\frac{5}{6}\),
Explanation:
Given to find \(\frac{1}{6}\) + \(\frac{2}{3}\) = ,
As both denominators are different first we need to
make common denominators means we need to multiply
numerator and denominator by 2 as
\(\frac{2}{3}\) X 2 = \(\frac{2 X 2}{3 X 2}\) =
\(\frac{4}{6}\) now we add as
\(\frac{1}{6}\) + \(\frac{4}{6}\) as
denominators are common as 6 we add numerators as
\(\frac{1 + 4}{6}\) = \(\frac{5}{6}\),
therefore common denominator is 6 and
Number sentence: \(\frac{1}{6}\) + \(\frac{4}{6}\) =
\(\frac{5}{6}\).
Practice
Estimate. Then solve using U.S. traditional multiplication.
Show your work on the back of this page.
Question 4.
723 ∗ 89 = __64,347________
Estimate: ___723 X 89 = 64,347_______
Answer:
723 X 89 = 64,347,
Estimate : 723 X 89 =64,347,
Explanation:
Estimate : 723 X 89 = 64,347,
So 723 X 89 =
723
X 89
6507
57840
64,347
Question 5.
1,20 7 ∗ 54 = ___65,178_______
Estimate: ___1,20 7 ∗ 54 = 65,178_______
Answer:
1,207 X 54 = 65,178,
Estimate: 1,20 7 ∗ 54 = 65,178,
Explanation:
Estimate : 1,207 X 54 =65,178,
So 723 X 89 =
1,207
X 54
4828
60350
65,178
Everyday Math Grade 5 Home Link 5.2 Answer Key
Using a Common Denominator
Question 1.
For each pair of fractions in the table, find a common denominator. Then rewrite the two fractions as equivalent fractions with a common denominator. Write > or < in the space provided to create a true number sentence.
Remember the three strategies you have learned:
- List equivalent fractions.
- Check to see if one denominator is a multiple of the other denominator.
- Multiply denominators to get a quick common denominator.
Answer:
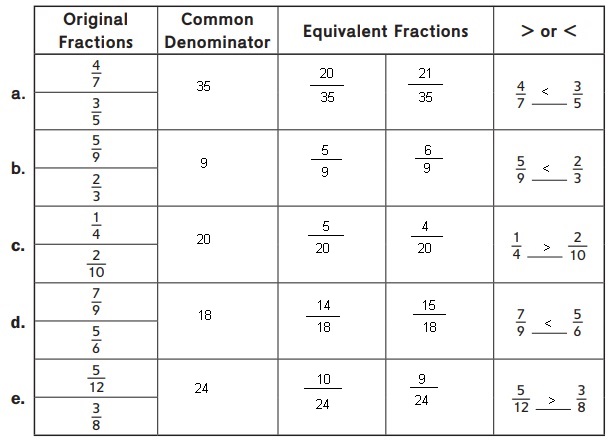
Explanation:
For each pair of fractions in the table, found a common denominator.
Then rewrote the two fractions as equivalent fractions with a common denominator. Wrote > or < in the space provided to create a true number sentence as shown above as
a. Given \(\frac{4}{7}\) , \(\frac{3}{5}\)
As both denominators are different first we need to
make common denominators 35 means we need to multiply
numerator and denominator by 5 for \(\frac{4}{7}\) and
by 7 for \(\frac{3}{5}\) we get \(\frac{20}{35}\) and
\(\frac{21}{35}\), Now if we compare we get
\(\frac{20}{35}\) < \(\frac{21}{35}\), so
\(\frac{4}{7}\) < \(\frac{3}{5}\).
b. Given \(\frac{5}{9}\) , \(\frac{2}{3}\)
As both denominators are different first we need to
make common denominators 9 means we need to multiply
numerator and denominator by 3 for \(\frac{2}{3}\) we get \(\frac{6}{9}\),Now if we compare we get
\(\frac{5}{9}\) < \(\frac{6}{9}\),
\(\frac{5}{9}\) < \(\frac{2}{3}\).
c. Given \(\frac{1}{4}\) , \(\frac{2}{10}\)
As both denominators are different first we need to
make common denominators 20 means we need to multiply
numerator and denominator by 5 for \(\frac{1}{4}\) and
by 2 for \(\frac{2}{10}\) we get \(\frac{5}{20}\) and
\(\frac{4}{20}\), Now if we compare we get
\(\frac{5}{20}\) > \(\frac{4}{20}\), so
\(\frac{1}{4}\) < \(\frac{2}{10}\).
d. Given \(\frac{7}{9}\) , \(\frac{5}{6}\)
As both denominators are different first we need to
make common denominators 18 means we need to multiply
numerator and denominator by 2 for \(\frac{7}{9}\) and
by 3 for \(\frac{5}{6}\) we get \(\frac{14}{18}\) and
\(\frac{15}{18}\), Now if we compare we get
\(\frac{14}{18}\) < \(\frac{15}{18}\), so
\(\frac{7}{9}\) < \(\frac{5}{6}\).
e. Given \(\frac{5}{12}\) , \(\frac{3}{8}\)
As both denominators are different first we need to
make common denominators 24 means we need to multiply
numerator and denominator by 2 for \(\frac{5}{12}\) and
by 3 for \(\frac{3}{8}\) we get \(\frac{10}{24}\) and
\(\frac{9}{24}\), Now if we compare we get
\(\frac{10}{24}\) > \(\frac{9}{24}\), so
\(\frac{5}{12}\) > \(\frac{3}{8}\).
Use the table to help you rewrite the problems with
common denominators. Then solve.
Question 2.
\(\frac{3}{5}\) – \(\frac{4}{7}\) = _________ – ________ = __________
Answer:
\(\frac{3}{5}\) – \(\frac{4}{7}\) =\(\frac{21}{35}\) – \(\frac{20}{35}\) =\(\frac{1}{35}\),
Explanation:
Used the table to help me to rewrite the problems with
common denominators as given
\(\frac{3}{5}\) – \(\frac{4}{7}\) =
As both denominators are different first we need to
make common denominators 35 means we need to multiply
numerator and denominator by 7 for \(\frac{3}{5}\)
and by 5 for \(\frac{4}{7}\) we get \(\frac{21}{35}\) and
\(\frac{20}{35}\), Now we subtract we get
\(\frac{21}{35}\) – \(\frac{20}{35}\), as we have
common denominators we subtract denominators as
\(\frac{21-20}{35}\) =\(\frac{1}{35}\).
Question 3.
\(\frac{1}{4}\) + \(\frac{2}{10}\) = _________ – ________ = __________
Answer:
\(\frac{1}{4}\) + \(\frac{2}{10}\) =
\(\frac{5}{20}\) + \(\frac{4}{20}\) =\(\frac{9}{20}\),
Explanation:
Used the table to help me to rewrite the problems with
common denominators as given
\(\frac{1}{4}\) +\(\frac{2}{10}\) =
As both denominators are different first we need to
make common denominators 20 means we need to multiply
numerator and denominator by 5 for \(\frac{1}{4}\) and
by 2 for \(\frac{2}{10}\) we get \(\frac{5}{20}\) and
\(\frac{4}{20}\), Now we add numerators as we have common
denominators we get \(\frac{5 + 4}{20}\) = \(\frac{9}{20}\).
Question 4.
\(\frac{5}{9}\) + \(\frac{2}{3}\) = _________ – ________ = __________
Answer:
\(\frac{5}{9}\) + \(\frac{2}{3}\) =
\(\frac{5}{9}\) + \(\frac{6}{9}\) =
\(\frac{11}{9}\) or 1\(\frac{2}{9}\),
Explanation:
Used the table to help me to rewrite the problems with
common denominators as given
\(\frac{5}{9}\) +\(\frac{2}{3}\) =
As both denominators are different first we need to
make common denominators 9 means we need to multiply
numerator and denominator by 3 for \(\frac{2}{3}\)
we get \(\frac{6}{9}\), Now we add numerators as we have common denominators as \(\frac{5 + 6}{9}\) = \(\frac{11}{9}\) as numerator is greater than denominator
we write in mixed fraction as (1 X 9 + 2 by 9), So
\(\frac{5}{9}\) + \(\frac{2}{3}\) =
\(\frac{5}{9}\) + \(\frac{6}{9}\) =
\(\frac{11}{9}\) or 1\(\frac{2}{9}\).
Practice
Solve. Show your work on the back of the page.
Question 5.
8,170 ÷ 75 → ___108 R70______
Answer:
8,170 ÷ 75 = 108 R70,
Explanation:
Given to solve 8,170 ÷ 75 =
108
75)8,170(
750
670
600
70
Therefore, 8,170 ÷ 75 = 108 R70.
Question 6.
298 ÷ 17 → ___17R9______
Answer:
298 ÷ 17 = 17 R9,
Explanation:
Given to solve 298 ÷ 17 =
17
17)298(
17
128
119
9
Therefore, 298 ÷ 17 = 17 R9.
Everyday Mathematics Grade 5 Home Link 5.3 Answers
Adding Fractions and Mixed Numbers
Estimate and then solve. Show your work.
Use your estimates to check your answers.
Remember: Before adding fractions and mixed numbers
with different denominators, you must rename one or
both fractions so both fractions have a common denominator.
Example: 2\(\frac{3}{5}\) + 4 \(\frac{2}{3}\) = ?
- Find a common denominator for the fraction parts.
The quick common denominator for \(\frac{3}{5}\) and \(\frac{2}{3}\) is the product of the
denominators, 5 ∗ 3, or 15. - Use the multiplication rule for equivalent fractions to rename each fraction so both fractions have the common denominator.
- Add.
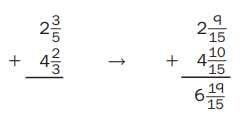
- Rename the sum. 6\(\frac{19}{15}\) = 6 + \(\frac{15}{15}\) + \(\frac{4}{15}\) = 6 + 1 \(\frac{4}{15}\) = 7 + \(\frac{4}{15}\) = 7\(\frac{4}{15}\)
Question 1.
Estimate: ___5\(\frac{5}{6}\) ______
3\(\frac{4}{6}\) + 2\(\frac{1}{6}\) = __________
Answer:
3\(\frac{4}{6}\) + 2\(\frac{1}{6}\) = 5\(\frac{5}{6}\),
Explanation:
Given to solve 3\(\frac{4}{6}\) + 2\(\frac{1}{6}\) =
both have common denominators as 6, So
3\(\frac{4}{6}\) = \(\frac{18 + 4}{6}\) =
\(\frac{22}{6}\) and 2\(\frac{1}{6}\) =
\(\frac{12 + 1}{6}\) = \(\frac{13}{6}\),
now we add \(\frac{22}{6}\) + \(\frac{13}{6}\) =
as both have common denominators 6 we add numerators as
\(\frac{22 + 13}{6}\) = \(\frac{35}{6}\) as
numerator is greater than denominator we write in
mixed fraction as (5 X 6 + 5 by 6) = 5\(\frac{5}{6}\),
therefore, 3\(\frac{4}{6}\) + 2\(\frac{1}{6}\) = 5\(\frac{5}{6}\).
Question 2.
Estimate: _________
6\(\frac{1}{3}\) + 2\(\frac{1}{6}\) = __________
Answer:
6\(\frac{1}{3}\) + 2\(\frac{1}{6}\) =
\(\frac{19}{3}\) + \(\frac{13}{6}\) =
\(\frac{38}{6}\) + \(\frac{13}{6}\) =
\(\frac{51}{6}\) = 8\(\frac{3}{6}\),
Explanation:
Given to solve 6\(\frac{1}{3}\) + 2\(\frac{1}{6}\) =
first we write mixed fraction into fraction as
6\(\frac{1}{3}\) = \(\frac{18 + 1}{3}\) =
\(\frac{19}{3}\) and 2\(\frac{1}{6}\) =
\(\frac{12 + 1}{6}\) = \(\frac{13}{6}\),
Now we need to make both common denominators as 6 so
we need to multiply numerator and denominator by 2 for
\(\frac{19}{3}\) we get \(\frac{19}{3}\) X 2 =
\(\frac{38}{6}\) , now we add \(\frac{38}{6}\) + \(\frac{13}{6}\) as both have common denominators 6
we add numerators as \(\frac{38 + 13}{6}\) = \(\frac{51}{6}\) as numerator is greater than denominator we write in
mixed fraction as (8 X 6 + 3 by 6) = 8\(\frac{3}{6}\),
therefore, 6\(\frac{1}{3}\) + 2\(\frac{1}{6}\) =
\(\frac{51}{6}\) = 8\(\frac{3}{6}\).
Question 3.
Estimate: ___________
\(\frac{3}{4}\) + \(\frac{7}{12}\) = ____________
Answer:
\(\frac{3}{4}\) + \(\frac{7}{12}\) =
\(\frac{16}{12}\) = 1\(\frac{4}{12}\),
Explanation:
Given to solve \(\frac{3}{4}\) + \(\frac{7}{12}\),
Now we need to make both common denominators as 12 so
we need to multiply numerator and denominator by 3 for
\(\frac{3}{4}\) we get \(\frac{3}{4}\) X 3 =
\(\frac{9}{12}\) , now we add \(\frac{9}{12}\) + \(\frac{7}{12}\) as both have common denominators 12
we add numerators as \(\frac{9 + 7}{12}\) = \(\frac{16}{12}\) as numerator is greater than denominator we write in
mixed fraction as (1 X 12 + 4 by 12) = 1\(\frac{4}{12}\),
therefore, \(\frac{3}{4}\) + \(\frac{7}{12}\) =
\(\frac{16}{12}\) = 1\(\frac{4}{12}\).
Question 4.
Estimate: ____________
15\(\frac{1}{2}\) + 12\(\frac{2}{5}\) = _________
Answer:
15\(\frac{1}{2}\) + 12\(\frac{2}{5}\) =
\(\frac{31}{2}\) + \(\frac{62}{5}\) =
\(\frac{155}{10}\) + \(\frac{124}{10}\) =
\(\frac{279}{10}\) = 27\(\frac{9}{10}\),
Explanation:
Given to solve 15\(\frac{1}{2}\) + 12\(\frac{2}{5}\) =
first we write mixed fraction into fraction as
15\(\frac{1}{2}\) = \(\frac{30 + 1}{2}\) =
\(\frac{31}{2}\) and 12\(\frac{2}{5}\) =
\(\frac{60 + 2}{5}\) = \(\frac{62}{5}\),
Now we need to make both common denominators as 10 so
we need to multiply numerator and denominator by 5 for
\(\frac{31}{2}\) we get \(\frac{31}{2}\) X 5 =
\(\frac{155}{10}\) and \(\frac{62}{5}\) by 2 we get
\(\frac{124}{10}\) now we add \(\frac{155}{10}\) + \(\frac{124}{10}\) as both have common denominators 10
we add numerators as \(\frac{155 + 124}{10}\) = \(\frac{279}{10}\) as numerator is greater than denominator we write in
mixed fraction as (27 X 10 + 9 by 10) = 27\(\frac{9}{10}\),
therefore, 15\(\frac{1}{2}\) + 12\(\frac{2}{5}\) =
\(\frac{31}{2}\) + \(\frac{62}{5}\) =
\(\frac{155}{10}\) + \(\frac{124}{10}\) =
\(\frac{279}{10}\) = 27\(\frac{9}{10}\).
Practice
Write each decimal using numerals.
Question 5.
three and six hundred twenty-four thousandths ___3.624____
Answer:
three and six hundred twenty-four thousandths = 3.624,
Explanation:
Given to write three and six hundred twenty-four thousandths
using numerals, So three and six hundred twenty-four thousandths =
3 + 6 X \(\frac{1}{100}\) + 24 X \(\frac{1}{1,000}\) =
3 + 0.6 + 0.024 = 3.624, therefore, three and
six hundred twenty-four thousandths = 3.624.
Question 6.
fourteen and twelve thousandths ____14.012________
Answer:
fourteen and twelve thousandths = 14.012,
Explanation:
Given to write fourteen and twelve thousandths
using numerals, So fourteen and twelve thousandths =
14 + 12 X \(\frac{1}{1,000}\) =
14 + 0.012 = 14.012, therefore, fourteen and
twelve thousandths = 14.012.
Write each decimal using words.
Question 7
1.46 ____________
Answer:
1.46 = one and forty-six hundredths,
Explanation:
Given to write 1.46 decimal in words as 1 is at
units place,4 is at tenths place and 6 at hundredths place,
therefore, 1.46 in words isone and forty-six hundredths.
Question 8.
4.309 ____________
Answer:
4.309 = four and three hundred and nine thousandths,
Explanation:
Given to write 4.309 decimal in words as 4 is at
units place and 309 is at hundred and thousandths place,
therefore, 4.309 = four and three hundred and nine thousandths.
Everyday Math Grade 5 Home Link 5.4 Answer Key
Marathon Training
Katie is training to run a marathon.
She keeps track of how many miles she runs each day.
Use the information in the table to answer the questions.
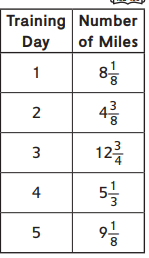
Question 1.
How many more miles did Katie run on Day 1 than on Day 2?
Number model: ____________
Estimate: ____________
Show your work: ____________
____________ miles
Answer:
Number model : 8\(\frac{1}{8}\) – 4\(\frac{3}{8}\),
Estimate : 8\(\frac{1}{8}\) – 4\(\frac{3}{8}\) =
\(\frac{65}{8}\) – \(\frac{35}{8}\) =
\(\frac{30}{8}\)miles or 3\(\frac{6}{8}\) miles
more miles did Katie ran on Day 1 than on Day 2,
Explanation:
Katie ran on Day 1 is 8\(\frac{1}{8}\) and
on Day 2 is 4\(\frac{3}{8}\), So miles did Katie run
on Day 1 than on Day 2 is 8\(\frac{1}{8}\) – 4\(\frac{3}{8}\), first we write mixed fractions in fractions as
8\(\frac{1}{8}\) = \(\frac{64 + 1}{8}\) = \(\frac{65}{8}\) and 4\(\frac{3}{8}\) = \(\frac{32 + 3}{8}\) =
\(\frac{35}{8}\), Now we subtract numerators as we
have common denominators as 8 so \(\frac{65}{8}\) – \(\frac{35}{8}\) = \(\frac{65 – 35}{8}\)miles =
\(\frac{30}{8}\)miles as numerator is greater than denomintor
we write in mixed fraction as (3 X 8 + 6 by 8) =
3\(\frac{6}{8}\) miles, therefore more miles did
Katie ran on Day 1 than on Day 2 is \(\frac{30}{8}\)miles or 3\(\frac{6}{8}\) miles.
Question 2.
How many miles did Katie run on Day 3 and Day 4 combined?
Number model: __12\(\frac{3}{4}\)miles +5\(\frac{1}{3}\) miles________
Estimate: ____________
Show your work: ____________
____________ miles
Answer:
Number model:
12\(\frac{3}{4}\)miles + 5\(\frac{1}{3}\) miles,
Estimate :
12\(\frac{3}{4}\)miles + 5\(\frac{1}{3}\) miles =
\(\frac{51}{4}\)miles + \(\frac{16}{3}\) miles =
\(\frac{217}{12}\)miles or 18\(\frac{1}{12}\) miles
did Katie run on Day 3 and Day 4 combinedly,
Explanation:
Katie ran on Day 3 is 12\(\frac{3}{4}\) and
on Day 4 is 5\(\frac{1}{3}\), So miles did Katie ran
on Day 3 and Day 4 combinedly is 12\(\frac{3}{4}\) +
5\(\frac{1}{3}\), first we write mixed fractions in fractions as
12\(\frac{3}{4}\) = \(\frac{48 + 3}{4}\) = \(\frac{51}{4}\) and 5\(\frac{1}{3}\) = \(\frac{15 + 1}{3}\) =
\(\frac{16}{3}\), Now we add them as
\(\frac{51}{4}\) + \(\frac{16}{3}\) =
\(\frac{51 X 3 + 16 X 4}{12}\)miles = \(\frac{153 + 64}{12}\) = \(\frac{217}{12}\)miles as numerator is greater than denomintor we write in mixed fraction as (18 X 12 + 1 by 12) =
18\(\frac{1}{12}\) miles, therefore more miles did
Katie ran on Day 3 and on Day 4 combinedly is \(\frac{217}{12}\)miles or 18\(\frac{1}{12}\) miles.
Question 3.
Katie set a goal to run 4 \(\frac{1}{2}\) miles on Day 5.
How much farther than her goal did she run?
Number model: ____________
Estimate: ____________
Show your work: ____________
____________ miles
Answer:
Number model : 9\(\frac{1}{8}\) – 4\(\frac{1}{2}\),
Estimate : 9\(\frac{1}{8}\) – 4\(\frac{1}{2}\) =
\(\frac{73}{8}\) – \(\frac{9}{2}\) =
\(\frac{37}{8}\)miles or 4\(\frac{5}{8}\) miles
farther more miles did Katie ran on Day 5,
Explanation:
Katie ran on Day 5 is 9\(\frac{1}{8}\) and
Katie set a goal to run 4 \(\frac{1}{2}\) miles on Day 5
So farther more miles did Katie ran on Day 5 is
9\(\frac{1}{8}\) – 4\(\frac{1}{2}\), first we write mixed fractions in fractions as 9\(\frac{1}{8}\) = \(\frac{72 + 1}{8}\) = \(\frac{73}{8}\) and 4\(\frac{1}{2}\) = \(\frac{8 + 1}{2}\) = \(\frac{9}{2}\),
Now we subtract as \(\frac{73}{8}\) – \(\frac{9}{2}\) = \(\frac{73 – 36}{8}\)miles = \(\frac{37}{8}\)miles as numerator is greater than denomintor we write
in mixed fraction as (4 X 8 + 5 by 8) = 4\(\frac{5}{8}\) miles, therefore more miles did Katie ran on Day 5 than
her setted goal is \(\frac{37}{8}\)miles or 4\(\frac{5}{8}\) miles.
Practice
Choose from the list above. Write the number that has:
Question 4.
a 7 in the hundredths place.
Answer:
128.174
Explanation:
Choosing from the list the number that has
a 7 in the hundredths place is in 128.174.
Question 5.
a 5 in the thousandths place.
Answer:
1,737.405,
Explanation:
Choosing from the list the number that has
a 5 in the thousandths place is in 1,737.405.
Question 6.
a 2 that is worth 0.2.
Answer:
8.25,
Explanation:
Choosing from the list the number that has
a 2 that is worth 0.2 is 8.25.
Everyday Mathematics Grade 5 Home Link 5.5 Answers
Fraction-Of Problems
Solve each fraction-of problem. Include a unit in your answer.
Then write a multiplication number model for each problem.
Question 1.
Suri made 6 gallons of lemonade to sell at her lemonade stand.
In one day she sold \(\frac{2}{3}\) of the lemonade.
How much lemonade did she sell?
Number model: _________
Answer:
Suri sells 4 gallons of lemonade,
Number model : \(\frac{2}{3}\) X 6 =4,
Explanation:
Given Suri made 6 gallons of lemonade to sell
at her lemonade stand.
In one day she sold \(\frac{2}{3}\) of the lemonade.
So lemonade did Suri sell is \(\frac{2}{3}\) X 6 =
\(\frac{2 X 6}{3}\) = \(\frac{12}{3}\) = 4 gallons,
therefore, Suri sells 4 gallons of lemonade and
Number model : \(\frac{2}{3}\) X 6 = 4.
Question 2.
Antonio planned to read 15 books over the summer
for the library’s summer reading challenge.
At the end of July he had read \(\frac{4}{5}\) of the books.
How many books had he read?
Number model: _________
Answer:
Antonio read 12 books,
Number model : \(\frac{4}{5}\) X 15 = 12,
Explanation:
Given Antonio planned to read 15 books over the summer
for the library’s summer reading challenge.
At the end of July he had read \(\frac{4}{5}\) of the books.
So number of many books had he read is
\(\frac{4}{5}\) X 15 = \(\frac{4 X 15}{5}\) =
\(\frac{60}{5}\) = 12, therefore Antonio read 12 books,
Number model : \(\frac{4}{5}\) X 15 = 12.
Question 3.
Elliot is riding in a 100-mile bike race to raise money for a charity.
So far he has completed \(\frac{7}{10}\) of the race.
How far has Elliot biked?
Number model: _________
Answer:
Elliot has biked 70 miles,
Number model : \(\frac{7}{10}\) X 100 = 70,
Explanation:
Given Elliot is riding in a 100-mile bike race to raise money for a charity.
So far he has completed \(\frac{7}{10}\) of the race.
So far has Elliot biked is \(\frac{7}{10}\) X 100 =
\(\frac{7 X 100}{10}\) = \(\frac{700}{10}\) = 70,
therefore, Elliot has biked 70 miles,
Number model : \(\frac{7}{10}\) X 100 = 70.
Question 4.
Erica’s garden has an area of 24 square feet.
She will use \(\frac{3}{4}\) of the space for
vegetables and \(\frac{1}{4}\) of the space for flowers.
How much space will she use for vegetables?
Number model: _________
Answer:
Erica’s used space for vegetables is 18 square feet,
Number model : \(\frac{3}{4}\) X 24 = 18,
Explanation:
Given Erica’s garden has an area of 24 square feet.
She will use \(\frac{3}{4}\) of the space for
vegetables and \(\frac{1}{4}\) of the space for flowers.
So space will she use for vegetables is \(\frac{3}{4}\) X 24 =
\(\frac{3 X 24}{4}\) = \(\frac{72}{4}\) =18 square feet,
therefore, Erica’s used space for vegetables is 18 square feet,
Number model : \(\frac{3}{4}\) X 24 = 18.
Practice
Write <, >, or = to make true number sentences.
Question 5.
0.3 ____<_____ 0.32
Answer:
0.3 < 0.32,
Explanation:
Given 0.3 and 0.32,
True number sentence: 0.3 < 0.32.
Question 6.
0.428 ____<_____ 0.43
Answer:
0.428 < 0.43,
Explanation:
Given 0.428 and 0.43,
True number sentence: 0.428 < 0.43.
Question 7.
1.68 ____=_____ 1.680
Answer:
1.68 = 1.680,
Explanation:
Given 1.68 and 1.680,
True number sentence: 1.68 = 1.680.
Question 8.
2.988 ___>____ 1.989
Answer:
2.988 > 1.989,
Explanation:
Given 2.988 and 1.989,
True number sentence: 2.988 > 1.989.
Question 9.
0.06 ____>_____ 0.006
Answer:
0.06 > 0.006,
Explanation:
Given 0.06 and 0.006,
True number sentence: 0.06 < 0.006.
Question 10.
5.64 ____>_____ 5.46
Answer:
5.64 > 5.46,
Explanation:
Given 5.64 and 5.46,
True number sentence: 5.64 > 5.46.
Everyday Math Grade 5 Home Link 5.6 Answer Key
Multiplying Whole Numbers and Fractions
Question 1.
a. What is 199–200 \(\frac{1}{6}\) of 18? _________
b. What is \(\frac{4}{6}\) of 18? _________
c. Fill in the blank to make a true number sentence.
18 ∗ \(\frac{4}{6}\) = _________
Answer:
a. 3,
b. 12,
c.12,
Explanation:
Given to find thw values of
a. (199 – 200) \(\frac{1}{6}\) of 18 =
(199 – 200)\(\frac{1}{6}\) X 18 =
1 X \(\frac{1 X 18}{6}\) =
1 X \(\frac{18}{6}\) =1 X 3 = 3.
b. \(\frac{4}{6}\) of 18 =
\(\frac{4}{6}\) X 18 =
\(\frac{4 X 18}{6}\) =
\(\frac{72}{6}\) =12.
c. 18 ∗ \(\frac{4}{6}\) =
\(\frac{18 X 4}{6}\) =
\(\frac{72}{6}\) = 12.
Question 2.
a. What is 15 ∗ 3? ____45_____
b. What is 45 ÷ 8? ___5 R5______
c. What is 15 ∗ 3 ÷ 8? ___5 R5______
d. Fill in the blank to make a true number sentence.
15 ∗ \(\frac{3}{8}\) = ___5 R5______
Answer:
a. 15 X 3 = 45,
b. 45 ÷ 8 = 5 R5,
c. 15 X 3 ÷ 8 = 5 R5,
d. 15 ∗ \(\frac{3}{8}\) = 5 R5,
Explanation:
a. Given to find 15 X 3 = 45,
so multiplying 15 by 3 we get 45.
b. 45 ÷ 8 =
5 R5
8)45(
40
5 _
Therfore, 45 ÷ 8 = 5 R5.
c. 15 X 3 ÷ 8 =
45 ÷ 8 =
5 R5
8)45(
40
5 _
Therfore, 15 X 3 ÷ 8 = 5 R5.
d. 15 ∗ \(\frac{3}{8}\) =
\(\frac{15 X 3}{8}\) =
\(\frac{45}{8}\) =
5 R5
8)45(
40
5 _
Therfore, 15 ∗ \(\frac{3}{8}\) = 5 R5.
Question 3.
The art teacher has 7 bottles of glue that are each \(\frac{2}{5}\) full. He combines them so he will have fewer bottles.
How many bottles of glue does he have after he combines them?
Number model: _7 X \(\frac{2}{5}\)________
__ \(\frac{14}{5}\) or 2\(\frac{4}{5}\)_______ bottles
Answer:
Number model: 7 X \(\frac{2}{5}\),
\(\frac{14}{5}\) or 2\(\frac{4}{5}\) bottles
of glue he have after he combines them,
Explanation:
Given the art teacher has 7 bottles of glue that are each \(\frac{2}{5}\) full. He combines them so he will have fewer bottles.
2So number of bottles of glue does he have after
he combines themis 7 X \(\frac{2}{5}\) =
\(\frac{7 X 2}{5}\) = \(\frac{14}{5}\) as
numerator is greater than denominator we write in mixed fraction
as (2 X 5 + 4 by 5) =2\(\frac{4}{5}\),
Therefore, Number model: 7 X \(\frac{2}{5}\),
\(\frac{14}{5}\) or 2\(\frac{4}{5}\) bottles
of glue he have after he combines them.
Question 4.
The librarian needs to return 24 books to the shelf.
In one hour she finished \(\frac{3}{4}\) of the job.
How many books has she returned to the shelf so far?
Number model: ____24 X \(\frac{3}{4}\),_____
______18____ books
Answer:
24 X \(\frac{3}{4}\),
18 books she has returned to the shell so far,
Explanation:
Given the librarian needs to return 24 books to the shelf.
In one hour she finished \(\frac{3}{4}\) of the job.
Number of books has she returned to the shelf so far are
24 X \(\frac{3}{4}\) = \(\frac{24 X 3}{4}\) =
\(\frac{72}{4}\) = 18, therefore 18 books she
has returned to the shell so far.
Practice
For Problems 5–7, round each decimal to the nearest tenth.
Question 5.
0.93 ___0.9____
Answer:
0.93 the nearest tenth is 0.9,
Explanation:
Rounded the decimal 0.93 to the nearest tenth is 0.9.
Question 6.
0.417 ___0.4____
Answer:
0.417 the nearest tenth is 0.4,
Explanation:
Rounded the decimal 0.417 to the nearest tenth is 0.4.
Question 7.
7.06 ___7.1_____
Answer:
7.06 the nearest tenth is 7.1,
Explanation:
Rounded the decimal 7.06 to the nearest tenth is 7.1.
For Problems 8–10, round each decimal to the nearest hundredth.
Question 8.
1.482 __1.48_____
Answer:
1.482 the nearest hundredth is 1.48,
Explanation:
Rounded the decimal 1.482 the nearest hundredth is 1.48.
Question 9.
5.715 ____5.72_____
Answer:
5.715 the nearest hundredth is 5.72,
Explanation:
Rounded the decimal 5.715 the nearest hundredth is 5.72.
Question 10.
2.996 ___3.00_____
Answer:
2.996 the nearest hundredth is 3.00,
Explanation:
Rounded the decimal 2.996 the nearest hundredth is 3.00.
Everyday Mathematics Grade 5 Home Link 5.7 Answers
Finding Fractions of Fractions
Follow the directions to solve the problems.
You will need two pieces of paper.
Question 1.
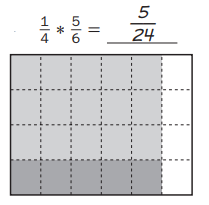
What is \(\frac{1}{3}\) of \(\frac{2}{4}\)?
a. Fold the paper into fourths. Unfold it and shade two of the fourths.
b. Fold the paper into thirds the other way, with the new folds crossing your folds from Part a. Unfold the paper and double-shade one -third of the shaded part.
c. Record what your paper looks like.
d. How much of the paper is double-shaded ? ____ \(\frac{2}{12}\)____
e. Fill in the blank: \(\frac{1}{3}\) of \(\frac{2}{4}\) is __ \(\frac{2}{12}\)_____.
Answer:
a.
Folded the paper into fourths, shaded two of the fourths,
b.
Folded the paper into thirds, doubled-shaded
one -third of the shaded part,
c. Recorded how it looks like on the paper,
d. \(\frac{2}{12}\),
e. \(\frac{2}{12}\),
Explanation:
Given to solve \(\frac{1}{3}\) of \(\frac{2}{4}\) =
\(\frac{2}{4}\) X \(\frac{1}{3}\) = \(\frac{2 X 1}{4 X 3}\) = \(\frac{2}{12}\),
a. Folded the paper into fourths.
Unfolded it and shaded two of the fourths as shown above,
b. Folded the paper into thirds the other way,
with the new folds crossing your folds from Part a.
Unfolded the paper and double-shaded one -third
of the shaded part as shown above.
c. Recorded how it looks like on the paper,
d. The amount of paper that is double-shaded
\(\frac{1}{3}\) of \(\frac{2}{4}\) =
\(\frac{2}{4}\) X \(\frac{1}{3}\) = \(\frac{2 X 1}{4 X 3}\) = \(\frac{2}{12}\).
e. \(\frac{1}{3}\) of \(\frac{2}{4}\) is
\(\frac{2}{4}\) X \(\frac{1}{3}\) = \(\frac{2 X 1}{4 X 3}\) = \(\frac{2}{12}\).
Question 2.
What is \(\frac{3}{4}\) of \(\frac{2}{3}\)?
a. Fold the paper into thirds. Unfold it and shade two of the thirds.
b. Fold the paper into fourths the other way, with the new folds crossing your folds from Part a. Unfold the paper and double-shade three-fourths of the shaded part.
c. Record what your paper looks like.
d. How much of the paper is double-shaded? ________
e. Fill in the blank: \(\frac{3}{4}\) of \(\frac{2}{3}\) is ________.
Answer:
a.
Folded the paper into thirds, shaded two of the thirds,
b.
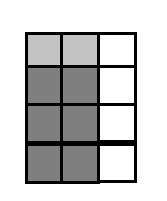
Folded the paper into fourths, double-shaded
three-fourths of the shaded part,
c. Recorded how it looks like on the paper,
d. \(\frac{6}{12}\),
e. \(\frac{6}{12}\),
Explanation:
Given to solve \(\frac{3}{4}\) of \(\frac{2}{3}\) =
\(\frac{3}{4}\) X \(\frac{2}{3}\) = \(\frac{3 X 2}{4 X 3}\) = \(\frac{6}{12}\),
a. Folded the paper into thirds.
Unfolded it and shaded two of the thirds as shown above,
b. Folded the paper into fourths the other way,
with the new folds crossing your folds from Part a.
Unfolded the paper and double-shaded three-fourths of
the shaded part as shown above.
c. Recorded how it looks like on the paper,
d. The amount of paper that is double-shaded
\(\frac{3}{4}\) of \(\frac{2}{3}\) =
\(\frac{3}{4}\) X \(\frac{2}{3}\) =
\(\frac{3 X 2}{4 X 3}\) = \(\frac{6}{12}\).
e. \(\frac{3}{4}\) of \(\frac{2}{3}\) is
\(\frac{3}{4}\) X \(\frac{2}{3}\) =
\(\frac{3 X 2}{4 X 3}\) = \(\frac{6}{12}\).
Practice
Make an estimate. Then solve.
Use your estimate to check whether your answer makes sense.
Question 3.
Answer:
Explanation:
Estimate : 1.42 + 3. 37 = 4.79,
Used my estimate to check whether my answer is true
as 1.42
+3.37
4.79, which is true.
Question 4.
Answer:
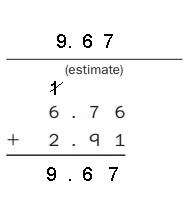
Explanation:
Estimate : 6.76 + 2.91 = 9.67,
Used my estimate to check whether my answer is true
as 6.76
+2.91
9.67, which is true.
Question 5.
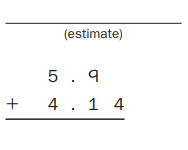
Answer:
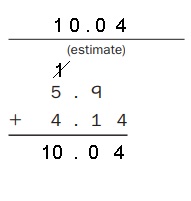
Explanation:
Estimate : 5.9 + 4.14 = 10.04,
Used my estimate to check whether my answer is true
as 5.9
+4.14
10.04, which is true.
Everyday Math Grade 5 Home Link 5.8 Answer Key
Using Area Models to Multiply Fractions
Label the blank tick marks on the number lines.
- Use the number lines to write the length and width of the shaded rectangle.
- Find the area of the shaded rectangle.
(The area of the big square is 1 square unit.)
Think: Into how many equal parts is the big square divided?
How many parts are shaded? - Write a multiplication number sentence for the area
of the shaded rectangle.
Question 1.
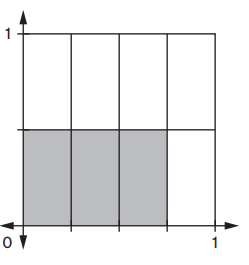
Length of shaded rectangle: __3/4______unit
Width of shaded rectangle: ___1/2_____unit
Area of shaded rectangle: ___3/8_____square unit
Number sentence: ____3/4____ × ___1/2_____ = ___3/8_____
Answer:
Length of shaded rectangle: 3/4 unit
Width of shaded rectangle: 1/2 unit
Area of shaded rectangle: 3/8 square unit
Number sentence: 3/4 × 1/2 = 3/8,
Explanation:
* Used the number lines to write the length and width of
the shaded rectangle as
Length of shaded rectangle: 3/4 unit
Width of shaded rectangle: 1/2 unit
* Founded the area of the shaded rectangle as
(The area of the big square is 1 square unit.)
Thinking: Into how many equal parts is the big square divided and
How many parts are shaded as
\(\frac{3}{4}\) X \(\frac{1}{2}\) =
\(\frac{3 X 1}{4 X 2}\) = \(\frac{3}{8}\),
* Wrote a multiplication number sentence for the area of the shaded rectangle as \(\frac{3}{4}\) X \(\frac{1}{2}\) =
\(\frac{3}{8}\) respectively.
Question 2.
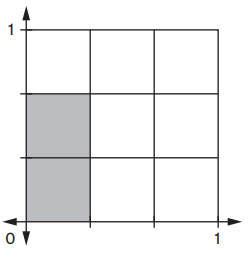
Length of shaded rectangle: ___1/3_____unit
Width of shaded rectangle: ___2/3_____unit
Area of shaded rectangle: ___2/9_____square unit
Number sentence: ___1/3_____ × ___2/3_____ = ___2/9_____
Answer:
Length of shaded rectangle: 1/3 unit
Width of shaded rectangle: 2/3 unit
Area of shaded rectangle: 2/9 square unit
Number sentence: 1/3 × 2/3 = 2/9,
Explanation:
* Used the number lines to write the length and width of
the shaded rectangle as
Length of shaded rectangle: 1/3 unit
Width of shaded rectangle: 2/3 unit
* Founded the area of the shaded rectangle as
(The area of the big square is 1 square unit.)
Thinking: Into how many equal parts is the big square divided and
How many parts are shaded as
\(\frac{1}{3}\) X \(\frac{2}{3}\) =
\(\frac{1 X 2}{3 X 3}\) = \(\frac{2}{9}\),
* Wrote a multiplication number sentence for the area of the shaded rectangle as \(\frac{1}{3}\) X \(\frac{2}{3}\) =
\(\frac{2}{9}\) respectively.
Practice
Make an estimate. Then solve. Use your estimate
to check whether your answer makes sense.
Question 3.
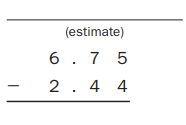
Answer:
Explanation:
Estimate : 6.75 – 2.44 = 4.31,
Used my estimate to check whether my answer is true
as 6.75
– 2.44
4.31, which is true.
Question 4.
Answer:
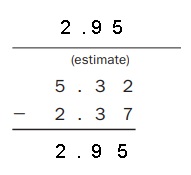
Explanation:
Estimate : 5.32 – 2.37 = 2.95,
Used my estimate to check whether my answer is true
as 5.32
– 2.37
2.95, which is true.
Question 5.
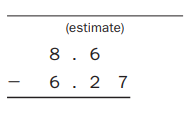
Answer:
Explanation:
Estimate : 8.6 – 6.27 = 2.33,
Used my estimate to check whether my answer is true
as 8.6
– 6.27
2.33, which is true.
Everyday Mathematics Grade 5 Home Link 5.9 Answers
Using an Algorithm to Multiply Fractions
A Fraction Multiplication Algorithm To multiply two fractions, multiply the numerators and multiply the denominators.
For example: \(\frac{2}{3} * \frac{3}{8}=\frac{(2 * 3)}{(3 * 8)}=\frac{6}{24}\)
For Problems 1–6, use the algorithm to multiply the fractions.
Question 1.
\(\frac{1}{3}\) * \(\frac{1}{2}\) = ___1/6______
Answer:
\(\frac{1}{3}\) * \(\frac{1}{2}\) = \(\frac{1}{3}\),
Explanation:
Multiplying the fractions \(\frac{1}{3}\) * \(\frac{1}{2}\) by multiplying the numerators and multiplying the denominators as
\(\frac{1 X 1}{3 X 2}\) = \(\frac{1}{6}\).
Question 2.
\(\frac{2}{4}\) * \(\frac{2}{3}\) = ____4/12_______
Answer:
\(\frac{2}{4}\) * \(\frac{2}{3}\) = \(\frac{4}{12}\),
Explanation:
Multiplying the fractions \(\frac{2}{4}\) * \(\frac{2}{3}\) by multiplying the numerators and multiplying the denominators as
\(\frac{2 X 2}{4 X 3}\) = \(\frac{4}{12}\).
Question 3.
\(\frac{4}{5}\) * \(\frac{2}{5}\) = ____8/25______
Answer:
\(\frac{2}{4}\) * \(\frac{2}{3}\) = \(\frac{4}{12}\),
Explanation:
Multiplying the fractions \(\frac{2}{4}\) * \(\frac{2}{3}\) by multiplying the numerators and multiplying the denominators as
\(\frac{2 X 2}{4 X 3}\) = \(\frac{4}{12}\).
Question 4.
\(\frac{2}{10}\) * \(\frac{2}{3}\) = _____4/30_____
Answer:
\(\frac{2}{10}\) * \(\frac{2}{3}\) = \(\frac{4}{30}\),
Explanation:
Multiplying the fractions \(\frac{2}{10}\) * \(\frac{2}{3}\) by multiplying the numerators and multiplying the denominators as
\(\frac{2 X 2}{10 X 3}\) = \(\frac{4}{30}\).
Question 5.
\(\frac{2}{8}\) * \(\frac{5}{6}\) = _____10/48______
Answer:
\(\frac{2}{8}\) * \(\frac{5}{6}\) = \(\frac{10}{48}\),
Explanation:
Multiplying the fractions \(\frac{2}{8}\) * \(\frac{5}{6}\) by multiplying the numerators and multiplying the denominators as
\(\frac{2 X 5}{8 X 6}\) = \(\frac{10}{48}\).
Question 6.
\(\frac{5}{12}\) * \(\frac{2}{7}\) = ____10/84_______
Answer:
\(\frac{5}{12}\) * \(\frac{2}{7}\) = \(\frac{10}{84}\),
Explanation:
Multiplying the fractions \(\frac{5}{12}\) * \(\frac{2}{7}\) by multiplying the numerators and multiplying the denominators as
\(\frac{5 X 2}{12 X 7}\) = \(\frac{10}{84}\).
Question 7.
If you multiply \(\frac{2}{3}\) ∗ \(\frac{6}{10}\), will the product be more than \(\frac{2}{3}\) or less than \(\frac{2}{3}\)? How do you know?
Answer:
Less than \(\frac{2}{3}\) by checking,
Explanation:
First we multiply \(\frac{2}{3}\) X \(\frac{6}{10}\) =
\(\frac{2 X 6}{3 X 10}\) = \(\frac{12}{30}\), Now
\(\frac{12}{30}\) = 0.4 and \(\frac{2}{3}\) = 0.66,
as 0.4 < 0.66, So \(\frac{12}{30}\) < \(\frac{2}{3}\).
Question 8.
If you multiply \(\frac{2}{3}\) ∗ \(\frac{6}{10}\), will the product be more than \(\frac{6}{10}\) or less than \(\frac{6}{10}\)? How do you know?
Answer:
Less than \(\frac{6}{10}\) by checking,
Explanation:
First we multiply \(\frac{2}{3}\) X \(\frac{6}{10}\) =
\(\frac{2 X 6}{3 X 10}\) = \(\frac{12}{30}\), Now
\(\frac{12}{30}\) = 0.4 and \(\frac{6}{10}\) = 0.6,
as 0.4 < 0.6, So \(\frac{12}{30}\) < \(\frac{6}{10}\).
In Problems 9–12, write true or false. Do not multiply.
Question 9.
\(\frac{3}{4}\) ∗ \(\frac{7}{10}\) is less than \(\frac{3}{4}\).
Answer:
True,
Explanation:
First we multiply \(\frac{3}{4}\) X \(\frac{7}{10}\) =
\(\frac{3 X 7}{4 X 10}\) = \(\frac{21}{40}\), Now
\(\frac{21}{40}\) = 0.525 and \(\frac{3}{4}\) = 0.75,
So true \(\frac{3}{4}\) ∗ \(\frac{7}{10}\) is less than \(\frac{3}{4}\).
Question 10.
\(\frac{7}{9}\) ∗ \(\frac{11}{12}\) is greater than \(\frac{11}{12}\).
Answer:
False,
Explanation:
First we multiply \(\frac{7}{9}\) X \(\frac{11}{12}\) =
\(\frac{7 X 11}{9 X 12}\) = \(\frac{77}{108}\), Now
\(\frac{77}{108}\) = 0.712 and \(\frac{11}{12}\) = 0.916,
So false as \(\frac{7}{9}\) ∗ \(\frac{11}{12}\) is not greater than \(\frac{11}{12}\).
Question 11.
\(\frac{4}{5}\) ∗ \(\frac{2}{8}\) is greater than\(\frac{2}{8}\) but less than \(\frac{4}{5}\).
Answer:
False,
Explanation:
First we multiply \(\frac{4}{5}\) X \(\frac{2}{8}\) =
\(\frac{4 X 2}{5 X 8}\) = \(\frac{8}{40}\), Now
\(\frac{8}{40}\) = 0.2, \(\frac{2}{8}\) = 0.25 and
\(\frac{4}{5}\) = 0.8,
So false as \(\frac{4}{5}\) ∗ \(\frac{2}{8}\) is not greater than \(\frac{2}{8}\) but less than \(\frac{4}{5}\).
Question 12.
\(\frac{6}{7}\) ∗ \(\frac{1}{4}\) is less than \(\frac{6}{7}\) and less than \(\frac{1}{4}\).
Answer:
True,
Explanation:
First we multiply \(\frac{6}{7}\) X \(\frac{1}{4}\) =
\(\frac{6 X 1}{7 X 4}\) = \(\frac{6}{28}\), Now
\(\frac{6}{28}\) = 0.214, \(\frac{6}{7}\) = 0. 857 and
\(\frac{1}{4}\) = 0.250,
So true as \(\frac{6}{7}\) ∗ \(\frac{1}{4}\) is less than \(\frac{6}{7}\) and also less than \(\frac{1}{4}\).
Practice
Question 13.
\(\frac{2}{3}\) + \(\frac{1}{6}\) = ___5/6_____
Answer:
\(\frac{2}{3}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\),
Explanation:
Given \(\frac{2}{3}\) + \(\frac{1}{6}\) before
adding as both denominators need to be same so we multiply
\(\frac{2}{3}\) by 2 before adding as \(\frac{2 x 2}{3 x 6}\) = \(\frac{4}{6}\), now denominators are same 6 so we add
numerators as \(\frac{4}{6}\) + \(\frac{1}{6}\) =
\(\frac{4 + 1}{6}\) = \(\frac{5}{6}\),
Therefore, \(\frac{2}{3}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\).
Question 14.
\(\frac{3}{4}\) + \(\frac{3}{8}\) = ___9/8 or 1_1/8_____
Answer:
\(\frac{3}{4}\) + \(\frac{3}{8}\) = \(\frac{9}{8}\) or 1\(\frac{1}{8}\),
Explanation:
Given \(\frac{3}{4}\) + \(\frac{3}{8}\) before
adding as both denominators need to be same so we multiply
\(\frac{3}{4}\) by 2 before adding as \(\frac{3 x 2}{4 x 2}\) = \(\frac{6}{8}\), now denominators are same 8 so we add
numerators as \(\frac{6}{8}\) + \(\frac{3}{8}\) =
\(\frac{6 + 3}{8}\) = \(\frac{9}{8}\),
as numerator is greater we can write in mixed fraction as
(1 X 8 + 1 by 8) = 1\(\frac{1}{8}\),
Therefore, \(\frac{3}{4}\) + \(\frac{3}{8}\) = \(\frac{9}{8}\) or 1\(\frac{1}{8}\).
Question 15.
\(\frac{2}{5}\) + \(\frac{1}{4}\) = ___13/20_____
Answer:
\(\frac{2}{5}\) + \(\frac{1}{4}\) = \(\frac{13}{20}\),
Explanation:
Given \(\frac{2}{5}\) + \(\frac{1}{4}\) before
adding as both denominators need to be same so we
multiply numerator and denominator by 4 to\(\frac{2}{5}\) before adding as \(\frac{2 x 4}{5 x 4}\) = \(\frac{8}{20}\) and \(\frac{1}{4}\) by 5 before adding as \(\frac{1 x 5}{4 x 5}\) = \(\frac{5}{20}\) now denominators are same 20 so we add numerators as \(\frac{8}{20}\) + \(\frac{5}{20}\) =
\(\frac{8 + 5}{20}\) = \(\frac{13}{20}\),
Therefore, \(\frac{2}{5}\) + \(\frac{1}{4}\) = \(\frac{13}{20}\).
Everyday Math Grade 5 Home Link 5.10 Answer Key
Mystery Models
Write a multiplication number sentence that represents the
amount of shaded space in the pictures below.
Add to the picture or create a new drawing to represent
your number sentence.
Question 1.
Answer:
\(\frac{1}{3}\) x \(\frac{2}{4}\) = \(\frac{2}{12}\) or
\(\frac{2}{4}\) x \(\frac{1}{3}\) = \(\frac{2}{12}\)
Explanation:
Wrote a multiplication number sentence that represents the
amount of shaded space in the picture as
\(\frac{1}{3}\) x \(\frac{2}{4}\) = \(\frac{1 X 2}{3 X 4}\) = \(\frac{2}{12}\),
Added to the picture to create a new drawing to represent
my number sentence as shown above.
Question 2.
Answer:
\(\frac{3}{4}\) x \(\frac{2}{5}\) = \(\frac{6}{20}\),
\(\frac{2}{5}\) x \(\frac{3}{4}\) = \(\frac{6}{20}\),
Explanation:
Wrote a multiplication number sentence that represents the
amount of shaded space in the picture as
\(\frac{3}{4}\) X \(\frac{2}{5}\) = \(\frac{3 X 2}{4 X 5}\) = \(\frac{6}{20}\),
Added to the picture to create a new drawing to represent
my number sentence as shown above.
Practice
Solve.
Question 3.
1\(\frac{1}{2}\) + 2\(\frac{2}{8}\) = __________
Answer:
1\(\frac{1}{2}\) + 2\(\frac{2}{8}\) = \(\frac{30}{8}\) or 3\(\frac{6}{8}\),
Explanation:
Given 1\(\frac{1}{2}\) + 2\(\frac{2}{8}\),
First we will write mixed fractions into fractions as 1\(\frac{1}{2}\) = (1 X 2 + 1 by 2) = \(\frac{3}{2}\) and 2\(\frac{2}{8}\) =
(2 x 8 + 2 by 8) = \(\frac{18}{8}\), before
adding as both denominators need to be same so we
multiply numerator and denominator by 4 to \(\frac{3}{2}\)
before adding as \(\frac{3 x 4}{2 x 4}\) = \(\frac{12}{8}\) now denominators are same 8 so we add numerators as \(\frac{12}{8}\) + \(\frac{18}{8}\) =
\(\frac{12 + 18}{8}\) = \(\frac{30}{8}\),
as numerator is greater than denominator we write in
mixed fraction as (3 X 8 + 6 by 8) = 3\(\frac{6}{8}\),
Therefore, 1\(\frac{1}{2}\) + 2\(\frac{2}{8}\) = \(\frac{30}{8}\) or 3\(\frac{6}{8}\).
Question 4.
6 – 3\(\frac{1}{3}\) = ___2 2/3______
Answer:
6 – 3\(\frac{1}{3}\) = \(\frac{8}{3}\) or 2\(\frac{2}{3}\),
Explanation:
Given 6 – 3\(\frac{1}{3}\),
First we will write mixed fraction into fractions as 3\(\frac{1}{3}\) =
(3 X 3 + 1 by 3) = \(\frac{10}{3}\) before
subtracting as both denominators need to be same so we
multiply numerator and denominator by 3 to \(\frac{6}{1}\)
before adding as \(\frac{6 x 3}{1 x 3}\) = \(\frac{18}{3}\) now denominators are same 3 so we subtract numerators as \(\frac{18}{3}\) – \(\frac{10}{3}\) =
\(\frac{18 – 10}{3}\) = \(\frac{8}{3}\),
as numerator is greater than denominator we write in
mixed fraction as (2 X 3 + 2 by 3) = 2\(\frac{2}{3}\),
Therefore, 6 – 3\(\frac{1}{3}\) = \(\frac{8}{3}\) or 2\(\frac{2}{3}\),
Question 5.
1\(\frac{4}{9}\) + 5\(\frac{2}{3}\) = _________
Answer:
1\(\frac{4}{9}\) + 5\(\frac{2}{3}\) =
\(\frac{64}{9}\) or 7\(\frac{1}{9}\),
Explanation:
Given 1\(\frac{4}{9}\) + 5\(\frac{2}{3}\),
First we will write mixed fractions into fractions as 1\(\frac{4}{9}\) = (1 X 9 + 4 by 9) = \(\frac{13}{9}\) and 5\(\frac{2}{3}\) =
(5 x 3 + 2 by 3) = \(\frac{17}{3}\), before
adding as both denominators need to be same so we
multiply numerator and denominator by 3 to \(\frac{17}{3}\) before adding as \(\frac{17 x 3}{3 x 3}\) = \(\frac{51}{9}\) now denominators are same 9 so we add numerators as \(\frac{13}{9}\) + \(\frac{51}{9}\) =
\(\frac{13 + 51}{9}\) = \(\frac{64}{9}\),
as numerator is greater than denominator we write in
mixed fraction as (7 X 9 + 1 by 9) = 7\(\frac{1}{9}\),
Therefore, 1\(\frac{4}{9}\) + 5\(\frac{2}{3}\) =
\(\frac{64}{9}\) or 7\(\frac{1}{9}\).
Question 6.
8\(\frac{1}{3}\) – 3\(\frac{3}{4}\) = ___4 7/12_______
Answer:
8\(\frac{1}{3}\) – 3\(\frac{3}{4}\) =
\(\frac{55}{12}\) or 4\(\frac{7}{12}\),
Explanation:
Given 8\(\frac{1}{3}\) – 3\(\frac{3}{4}\),
First we will write mixed fractions into fractions as 8\(\frac{1}{3}\) = (8 X 3 + 1 by 3) = \(\frac{25}{3}\) and 3\(\frac{3}{4}\) =
(3 x 4 + 3 by 4) = \(\frac{15}{4}\), before
subtracting as both denominators need to be same so we
multiply numerator and denominator by 4 to \(\frac{25}{3}\) before subtracting as \(\frac{25 x 4}{3 x 4}\) = \(\frac{100}{12}\) and multiply numerator and denominator by 3 to \(\frac{15}{4}\) as \(\frac{15 X 3}{4 X 3}\) = \(\frac{45}{12}\) now denominators are same 12 so we subtract numerators as \(\frac{100}{12}\) – \(\frac{45}{12}\) =
\(\frac{100 – 45}{12}\) = \(\frac{55}{12}\),
as numerator is greater than denominator we write in
mixed fraction as (4 X 12 + 7 by 12) = 4\(\frac{7}{12}\),
Therefore, 8\(\frac{1}{3}\) – 3\(\frac{3}{4}\) =
\(\frac{55}{12}\) or 4\(\frac{7}{12}\).
Everyday Mathematics Grade 5 Home Link 5.11 Answers
Finding Equivalent Fractions
Question 1.
a. List three fractions that are equivalent to 1.
___2/2____, ___3/3____, ____5/5___
b. Use the fractions you wrote in Part a to find three
fractions equivalent to \(\frac{6}{7}\).
Example: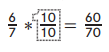 
_______, _______, _______
Answer:
a. \(\frac{2}{2}\), \(\frac{3}{3}\), \(\frac{5}{5}\),
b. \(\frac{24}{28}\), \(\frac{54}{63}\) and
\(\frac{150}{175}\),
Explanation:
a. Three fractions that are equivalent to 1 are
\(\frac{2}{2}\), \(\frac{3}{3}\), \(\frac{5}{5}\),
b. Using the fractions I wrote in Part a to find three
fractions equivalent to \(\frac{6}{7}\) are
\(\frac{24}{28}\), \(\frac{54}{63}\), \(\frac{150}{175}\) because as \(\frac{2}{2}\) X \(\frac{12}{14}\) = \(\frac{24}{28}\) = \(\frac{6}{7}\),
\(\frac{3}{3}\) X \(\frac{18}{21}\) = \(\frac{54}{63}\) = \(\frac{6}{7}\),
\(\frac{5}{5}\) X \(\frac{30}{35}\) = \(\frac{150}{175}\) =\(\frac{6}{7}\) respectively.
Question 2.
You are solving fraction addition problems.
Use the information to find equivalent fractions.
a. Original fraction: \(\frac{4}{5}\)
Denominator needed: 20
Multiply by: ____4/4______
Equivalent fraction: ____16/20_______
Answer:
Denominator needed: 20
Multiply by: \(\frac{4}{4}\)
Equivalent fraction: \(\frac{16}{20}\),
Explanation:
Given \(\frac{4}{5}\) the equivalent fraction is
as numerator is 4 so we multiply numerator and
denominator by 4 as \(\frac{4}{5}\) X \(\frac{4}{4}\) =
\(\frac{4 X 4}{5 X 4}\) = \(\frac{16}{20}\),
therefore denominator needed is 20,
Multiply by: \(\frac{4}{4}\) and
Equivalent fraction: \(\frac{16}{20}\).
b. Original fraction: \(\frac{1}{3}\)
Denominator needed: 18
Multiply by: ____6/6______
Equivalent fraction: ____6/18______
Answer:
Denominator needed: 18
Multiply by: \(\frac{6}{6}\)
Equivalent fraction: \(\frac{6}{18}\),
Explanation:
Given \(\frac{1}{3}\) the equivalent fraction is
as numerator is 6 so we multiply numerator and
denominator by 6 as \(\frac{1}{3}\) X \(\frac{6}{6}\) =
\(\frac{1 X 6}{3 X 6}\) = \(\frac{6}{18}\),
therefore denominator needed is 18,
Multiply by: \(\frac{6}{6}\) and
Equivalent fraction: \(\frac{6}{18}\).
Question 3.
Addison wanted to find a fraction equivalent to \(\frac{3}{8}\) with 16 in the denominator. He thought: “8 ∗ 2 = 16, so I need to multiply \(\frac{3}{8}\) by 2.” He got an answer of \(\frac{3}{16}\).
a. Is \(\frac{3}{16}\) equivalent to \(\frac{3}{8}\)? How do you know?
Answer:
No,
\(\frac{3}{16}\) ≠ \(\frac{3}{8}\),
Explanation:
Given Addison wanted to find a fraction equivalent to \(\frac{3}{8}\) with 16 in the denominator. He thought: “8 ∗ 2 = 16, so I need to multiply \(\frac{3}{8}\) by 2.” He got an answer of \(\frac{3}{16}\) but Addison is incorrect as \(\frac{3}{16}\)
is not equivalent to \(\frac{3}{8}\).
b. What mistake did Addison make?
Answer:
Addison multiplyed only denominator by 2 not numerator,
Explanation:
Given Addison wanted to find a fraction equivalent to \(\frac{3}{8}\) with 16 in the denominator. He thought: “8 ∗ 2 = 16, so I need to multiply \(\frac{3}{8}\) by 2.” He got an answer of \(\frac{3}{16}\) but Addison is incorrect as \(\frac{3}{16}\)
is not equivalent to \(\frac{3}{8}\) as he multipled
only denominator by 2 not numerator.
Practice
Solve.
Question 4.
What is \(\frac{2}{3}\) of 9?
Answer:
\(\frac{2}{3}\) of 9 is 6,
Explanation:
Given to solve \(\frac{2}{3}\) of 9,
So \(\frac{2}{3}\) X 9 = \(\frac{2 X 9}{3}\) =
\(\frac{18}{3}\) = 6.
Question 5.
What is \(\frac{3}{5}\) of 20?
Answer:
\(\frac{3}{5}\) of 20 is 12,
Explanation:
Given to solve \(\frac{3}{5}\) of 20,
So \(\frac{3}{5}\) X 20 = \(\frac{3 X 20}{5}\) =
\(\frac{60}{5}\) = 12.
Question 6.
Explain how you found your answer for Problem 5.
Answer:
Solving and multiplying \(\frac{3}{5}\) X 20,
Explanation:
By solving \(\frac{3}{5}\) X 20 \(\frac{3 X 20}{5}\) =
\(\frac{60}{5}\) = 12 I found the answer for Problem 5.
Everyday Math Grade 5 Home Link 5.12 Answer Key
Writing Fraction Multiplication Stories
Solve each multiplication problem. Then write a number
story that matches the number sentence and representation.
Example:
Number Story: Mr. Danielson had a tray of pumpkin bread that was \(\frac{5}{6}\) full. After sharing his bread with students, \(\frac{1}{4}\) of what he had brought was left.
What fraction of the whole tray was left?
Question 1.
4 ∗ \(\frac{2}{3}\) = _____8/3_ or 2 2/3____
Number Story: __________
Answer:
4 ∗ \(\frac{2}{3}\) = \(\frac{8}{3}\) or 2\(\frac{2}{3}\),
Number Story :
Our class has 4 groups each group have 10 children who can play
cricket, in that \(\frac{2}{3}\) of children participated
in the competition, So how many groups of children
participated in all?,
Explanation:
Given 4 ∗ \(\frac{2}{3}\) = \(\frac{4 X 2}{3}\) =
\(\frac{8}{3}\) or 2\(\frac{2}{3}\),
Number Story :
Our class has 4 groups each group have 10 children who can play
cricket, in that \(\frac{2}{3}\) of children participated
in the competition, So how many groups of children
participated in all? Wrote number story above.
Question 2.
\(\frac{1}{2}\) ∗ 16 = ___8______
Number Story: __________
Answer:
\(\frac{1}{2}\) X 16 = 8,
Number Story :
There are 16 books in library out which \(\frac{1}{2}\) of books
are moral stories, Therefore how many books are moral stories
in library?,
Explanation:
Given \(\frac{1}{2}\) X 16 = 8,
Number Story :
There are 16 books in library out which \(\frac{1}{2}\) of books
are moral stories, Therefore how many books are moral stories
in library?, Wrote number story above.
Practice
Make an estimate. Then add or subtract. Show your work on
the back of this page.
Question 3
4.79 + 2.03 = ?
Estimate: ____6.82______
4.79 + 2.03 = ___6.82_______
Answer:
Estimate: 6.82,
4.79 + 2.03 = 6.82,
Explanation:
My estimate is 6.82,
4.79
+2.03
6.82.
Question 4.
8.25 – 3.91 = ?
Estimate: ____4.34______
8.25 – 3.91 = __4.34________
Answer:
Estimate : 4.34,
8.25 – 3.91 = 4.34,
Explanation:
My estimate is 4.34,
8.25
-3.91
4.34.
Everyday Mathematics Grade 5 Home Link 5.13 Answers
Solving Fraction Division Problems
Write a number model using a letter for the unknown.
Solve, showing your solution strategy with representations or drawings. Summarize your work with a division number model.
Check your answer using multiplication and
write a number sentence to show how you checked.
Question 1.
Ben has \(\frac{1}{2}\) of a loaf of bread.
If he and his 3 friends share the \(\frac{1}{2}\) loaf equally,
how much of the whole loaf will each person get?
Number model: _____1/2 X 1/4 = 1/8_______
Each person will get __1/2_____ loaf of bread.
Answer:
Number model:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{2}\) X \(\frac{1}{4}\) = \(\frac{1}{8}\),
Each person will get \(\frac{1}{2}\) loaf of bread,
Explanation:
Given Ben has \(\frac{1}{2}\) of a loaf of bread.
If he and his 3 friends share the \(\frac{1}{2}\) loaf equally,
Part of the whole loaf will each person get is
Number model:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{2}\) X \(\frac{1}{4}\) = \(\frac{1}{8}\),
Each person will get \(\frac{1}{8}\) X 4 = [/latex] = \(\frac{4}{8}\) = \(\frac{1}{2}\) loaf of bread.
Question 2.
Amanda has a piece of ribbon that is \(\frac{1}{4}\) yard long.
She wants to share the ribbon with 2 friends so that they can each wear a ribbon for Breast Cancer Awareness Month.
If each of the 3 friends gets the same amount, how much
ribbon will each person get?
Number model: ____1/4 X 1/3 = 1/12______
Each person will get ___1/4_______ yard of ribbon.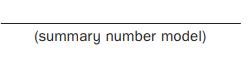 
Answer:
Number model:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{4}\) X \(\frac{1}{3}\) = \(\frac{1}{12}\),
Each person will get \(\frac{1}{4}\) yard of ribbon,
Explanation:
Given Amanda has a piece of ribbon that is \(\frac{1}{4}\) yard long. She wants to share the ribbon with 2 friends so that they can each wear a ribbon for Breast Cancer Awareness Month.
If each of the 3 friends gets the same amount,
Number model:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{4}\) X \(\frac{1}{3}\) = \(\frac{1}{12}\),
Each person will get ribbon is \(\frac{1}{12}\) X 3 =
\(\frac{3}{12}\) = \(\frac{1}{4}\).
Practice
Make an estimate. Then use U.S. traditional multiplication to solve.
Show your work on the back of this page.
Question 3.
Estimate: ___22,113_____
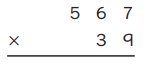
Answer:
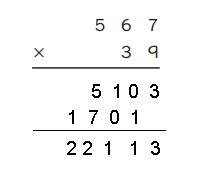
Explanation:
Given 567 X 39 =
Estimate = 567 X 39 =22,113 which is reasonable as shown above.
Question 4.
Estimate: ___71,568_____
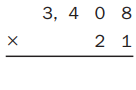
Answer:
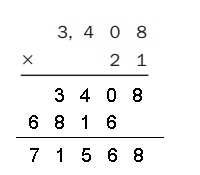
Explanation:
Given 3,408 X 21 =
Estimate = 3,408 X 21 =71,568 which is reasonable as shown above.
Everyday Math Grade 5 Home Link 5.14 Answer Key
More Fraction Division Problems
For Problems 1 and 2, write a number model using a
letter for the unknown. Solve, showing your solution strategy.
Summarize your work with a division number model.
Check your answer using multiplication, and
write a number sentence to show how you checked.
Question 1.
Charity is packing a 2-pound container of trail mix into
bags for a camping trip.
Each bag holds \(\frac{1}{8}\) pound of trail mix.
If Charity uses all 2 pounds of trail mix,
how many \(\frac{1}{8}\) pound bags will she have?
Number model: __2 ÷ 1/8 =16_______
Charity will have _____16 ,___ \(\frac{1}{8}\) pound bags.
Answer:
Number model: __2 ÷ \(\frac{1}{8}\) =16_______
Charity will have _____16 ,___ \(\frac{1}{8}\) pound bags,
Explanation:
Given Charity is packing a 2-pound container of trail mix into
bags for a camping trip.
Each bag holds \(\frac{1}{8}\) pound of trail mix.
If Charity uses all 2 pounds of trail mix then
Number model = 2 ÷\(\frac{1}{8}\) = 2 X 8 = 16,
Charity will have 16, \(\frac{1}{8}\) pound bags she will have.
Question 2.
Davis has a thin box that is 5 inches wide.
He wants to use the box to store markers that
are \(\frac{1}{2}\) inch wide. If he lines up
the markers side by side and uses the entire width of the box,
how many markers can Davis fit in the box?
Number model: __5 ÷ 1/2 =10________
Davis will be able to fit _____5_____ markers in the box. 
Answer:
Number model: 5 ÷ \(\frac{1}{2}\) = 10,
Davis will be able to fit 5 markers in the box,
Explanation:
Given Davis has a thin box that is 5 inches wide.
He wants to use the box to store markers that
are \(\frac{1}{2}\) inch wide. If he lines up
the markers side by side and uses the entire width of the box,
number of markers can Davis fit in the box are
5 ÷ \(\frac{1}{2}\) = 5 X 2 = 10,
So 10 X \(\frac{1}{2}\) = 5 markers in the box.
Practice
Make an estimate. Then solve. Show your work on the back of this page
Question 3.
623 ÷ 8 → ____77R7_______
Estimate: ___77R7_____
Answer:
623 ÷ 8 = 77 remainder 7,
Estimate: 77R7,
Explanation:
Given 623 ÷ 8 =
77 R 7
8)623(
56
63
56
7
So, 623 ÷ 8 = 77 remainder 7 and
estimate is also reasonable.
Question 4.
4,495 ÷ 50 → ___89R45________
Estimate: ___89R45________
Answer:
4,495 ÷ 50 = 89 remainder 45,
Estimate: 89R45,
Explanation:
Given 4,495 ÷ 50 =
89 R 45
50)4,495(
4,450
45
So, 4,495 ÷ 50 = 89 remainder 45 and
estimate is also reasonable.