Everyday Math Grade 5 Answers Unit 3 Fraction Concepts, Addition, and Subtraction

Everyday Mathematics 5th Grade Answer Key Unit 3 Fraction Concepts, Addition, and Subtraction

Everyday Mathematics Grade 5 Home Link 3.1 Answers

Modeling and Solving Fair Share Number Stories

Use a drawing to model each number story. Then solve.
Question 1.
You are sharing 2 loaves of bread with 5 friends. You want each person to get a fair share. How much bread will each person get?
Solution: __________
Model:
Answer:

Question 2.
Betsy and 3 of her friends are splitting a whole watermelon. There are 6 circular slices of watermelon. How many slices of watermelon will each person get?
Solution: __________
Model:
Answer:

Question 3.
Darius and Matthew have 3 fruit bars. They are both hungry after playing football and decide to split the fruit bars evenly. How much fruit bar will each boy get?
Solution: __________
Model:
Answer:

Practice
Make an estimate and solve. Show your work on the back of this page .
Question 4.

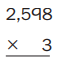
Estimate: ___________
Answer:

Question 5.

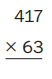
Estimate: ___________
Answer:

Everyday Math Grade 5 Home Link 3.2 Answer Key

Fair Share Problems with Number Models

Solve each number story. Draw a picture and write a number model to show how you solved each problem.
Question 1.
Mr. Chu is slicing 4 cantaloupes for his class. There are 24 students in the class. If Mr. Chu cuts the cantaloupes to make an equal portion for each student, how much of a whole cantaloupe will each student get?
___________ cantaloupe
Number model: __________
Answer:

Question 2.
Two classrooms are sharing 7 packages of unit cubes. If the packages are split evenly, how many packages will each classroom receive?
___________ packages
Number model: ___________
Answer:

Question 3.
Jane, Max, and Greg are splitting a 10-ounce bag of popcorn. If they share the popcorn equally, how many ounces of popcorn will each person get?
___________ ounces
Number model: ___________
Answer:

Practice
Question 4.
a. 540 ÷ 9 = ___________
b. 540 ÷ 90 = ___________
c. 5,400 ÷ 90 = ___________
Answer:

Question 5.
a. 320 ÷ 80 = ___________
b. 3,200 ÷ 8 = ___________
c. 32,000 ÷ 800 = ___________
Answer:

Everyday Mathematics Grade 5 Home Link 3.3 Answers

Division Number Stories with Remainders

For each number story, write a number model with a letter for the unknown. Then solve. You may draw a picture to help. Explain what you did with the remainder.
Question 1.
Ms. Davis’s class is having a picnic. There are 27 students in her class. If each picnic table seats 6 people, how many picnic tables will the class need so that all of the students and Ms. Davis have a seat?
Number model: ___________
Quotient: ___________ Remainder: ___________
Answer: They will need ___________ tables.
Circle what you did with the remainder.
Ignored it Reported it as a fraction Rounded the quotient up Why?
Answer:

Question 2.
Nolan brought 2 boxes of fruit bars to share
with his football team. There are 12 bars in
each box and 16 people on the team. If the
bars are shared equally, how many fruit bars
will each person get?
Number model: ___________
Quotient: ___________ Remainder: ___________
Answer: ___________
Circle what you did with the remainder.
Ignored it Reported it as a fraction Rounded the quotient up Why?
Answer:

Practice
Evaluate each expression.
Question 3.
8 + (6 ∗ 3) ___________
Answer:

Question 4.
(6 + 2) ∗ (9 – 5) ___________
Answer:

Question 5.
12 ÷ [3 ∗ (10 ÷ 5)] ___________
Answer:

Question 6.
{20 ÷ [7 + (6 ÷ 2)]} ∗ 5 ___________
Answer:

Everyday Math Grade 5 Home Link 3.4 Answer Key

Fractions on a Number Line

Question 1.
Divide this number line to show halves. Label each tick mark with a fraction.

Answer:

Question 2.
Divide this number line to show fourths. Label each tick mark with a fraction.

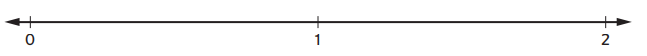
Answer:

Question 3.
Divide this number line to show eighths. Label each tick mark with a fraction.

Answer:

Use the number lines above or the Fraction Number Lines Poster to solve Problems 4–6.
Question 4.
Which number is greater? Circle the greater number in each pair.
a. \(\frac{3}{8}\) or \(\frac{1}{4}\)
b. \(\frac{2}{2}\) or \(\frac{5}{4}\)
c. 1\(\frac{5}{8}\) or \(\frac{3}{2}\)
Answer:

Question 5.
Rename each fraction as a mixed number.
a. \(\frac{6}{4}\) = _________
b. \(\frac{3}{2}\) = ___________
c. \(\frac{13}{8}\) = __________
Answer:

Question 6.
Rename each mixed number as a fraction.
a. 1\(\frac{2}{2}\) = ___________
b. 1\(\frac{6}{8}\) = ___________
c. 1\(\frac{1}{4}\) = ___________
Answer:

Practice
Question 7.
Write each number in standard notation.
a. 3 ∗ 102 = ___________
b. 5 ∗ 103 = ___________
c. 8 ∗ 104 =___________
Answer:

Question 8.
Write each number as a product, using exponential notation.
a. 900 = ___________
b. 6,000 = ___________
c. 70,000 = ___________
Answer:

Everyday Mathematics Grade 5 Home Link 3.5 Answers

More Fraction Top-It

Eddie and his friend are playing another version of Fraction Top-It. Each player turns over 4 number cards and places them as the digits on the gameboard. The player with the larger quotient wins the round.
Eddie’s cards are 2, 6, 3, and 4.
Question 1.
If you were Eddie, how would you place your cards? What is the quotient?

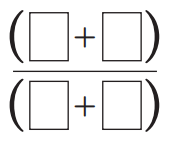
Answer:

Question 2.
What rule can Eddie use to create the largest possible fraction? Explain why this rule works.
Answer:

Practice
Question 3.
Write the value of the 3 in each of the following numbers.
a. 1,322,072 ___________
b. 8,236,914 ___________
c. 5,703,000 ___________
d. 4,091,316 ___________
e. 8,192,038 ___________
f. 7,025,943 ___________
Answer:

Everyday Math Grade 5 Home Link 3.6 Answer Key

Fractions and Number Sense

Question 1.
Josie calculated \(\frac{1}{5}\) + \(\frac{1}{2}\) and said the answer was \(\frac{2}{7}\). Explain how you know that Josie’s answer does not make sense.
Did you need to calculate an exact answer to know that Josie’s answer doesn’t make sense? Tell someone at home why you did or didn’t need to calculate an exact answer.
Answer:

Question 2.
Renee calculated \(\frac{3}{6}\) + \(\frac{2}{4}\) and said the answer was \(\frac{5}{10}\). Josie solved the same problem and said the answer was 1. Whose answer is more reasonable? Explain how you know.
Answer:

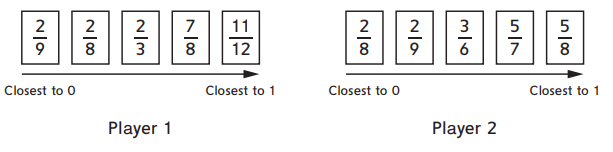
Question 3.
Two students are playing Build-It. To win, all 5 cards must be in order from smallest to largest. Circle the winning set of cards.

Answer:

Practice
Insert grouping symbols to make true number sentences.
Question 4.
6 × 4 + 1 = 30
Answer:

Question 5.
12 ÷ 3 × 2 – 1 = 1
Answer:

Question 6.
48 ÷ 6 + 5 × 3 = 39
Answer:

Question 7.
\(\frac{50}{10}\) + \(\frac{10}{2}\) = 5
Answer:

Everyday Mathematics Grade 5 Home Link 3.7 Answers

Estimating with Fractions

For Problems 1 and 2, circle the best estimate. Explain your estimation strategies to someone at home.
Question 1.
The sum of \(\frac{3}{4}\) and \(\frac{18}{19}\)is closest to _________.
0
1
2
Answer:

Question 2.
2\(\frac{3}{8}\) – \(\frac{3}{4}\) is _________
less than 2
greater than 2
Answer:

For Problems 3–5, refer to the number line below.

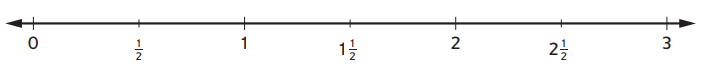
Question 3.
Henry ran 1\(\frac{5}{8}\) miles in the morning and \(\frac{9}{10}\) mile in the afternoon. About how many miles did he run in all? Place an X on the number line to show your estimate.
Answer:

Question 4.
Tia ran 2\(\frac{7}{8}\) miles. George ran 1\(\frac{1}{10}\) miles. About how many more miles did Tia run than George? Place a star on the number line to show your estimate.
Answer:

Question 5.
Explain how you estimated the difference in Problem 4.
Answer:

Practice
Use V = B × h or V = l × w × h to solve.
Question 6.
What is the volume of a box that is 14 inches long, 7 inches wide, and 10 inches high?
The volume of the box is ____________ cubic inches.
Number model: ________
Answer:

Question 7.
The floor of Raj’s classroom has an area of 525 feet. The ceiling is 12 feet high. What is the volume of Raj’s classroom?
The volume of the classroom is ____________ ft³.
Number model: ________
Answer:

Everyday Math Grade 5 Home Link 3.8 Answer Key

Renaming Fractions

You can make trades to find new names for mixed numbers and fractions greater than 1.
Example 1:

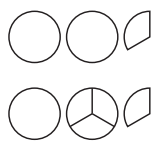
Start with 2\(\frac{1}{3}\).
Trade 1 whole for \(\frac{3}{3}\).
Now you have 1 whole and 4 thirds, or 1 \(\frac{4}{3}\).
Another name for 2 \(\frac{1}{3}\) is 1 \(\frac{4}{3}\)

Example 2:

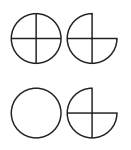
Start with \(\frac{7}{4}\)
Trade \(\frac{4}{4}\) for 1 whole.
Now you have 1 whole and 3 fourths, or 1 \(\frac{3}{4}\).
Another name for \(\frac{7}{4}\) is 1 \(\frac{3}{4}\)

In Problems 1 and 2, find at least one more name for each fraction or mixed number. Do not change the denominator. Check that your trades were fair and record the trades you made. You can use the pictures to help you think about making trades.
Question 1.
3 \(\frac{1}{2}\)

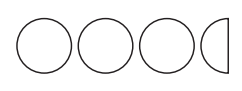
Name: _____________
Trade: _____________
Answer:

Question 2.
1 \(\frac{7}{6}\)

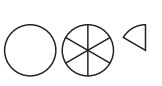
Name: _____________
Trade: _____________
Answer:

In Problems 3 and 4, cross out the fraction or mixed number that does not name the same number as the others in the group. You can draw pictures to help you.
Question 3.
4\(\frac{1}{8}\), \(\frac{33}{8}\), 3\(\frac{5}{8}\)
Answer:

Question 4.
3\(\frac{6}{4}\), 1\(\frac{10}{4}\), 4\(\frac{2}{4}\)
Answer:

Practice
Make an estimate and solve. Use the back of the paper if you need more space.
Question 5.
Estimate: __________

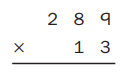
Answer:

Question 6.
Estimate: __________

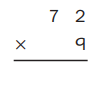
Answer:

Everyday Mathematics Grade 5 Home Link 3.9 Answers

Solving More Mixed-Number Stories

For each story:

• Write a number model with a letter for the unknown.
• Make an estimate.
• Solve. You can use a drawing or number line to help.
• Use your estimate to check whether your answer makes sense.

Question 1.
To make purple paint, Stephen mixed 1 \(\frac{1}{4}\) gallons of red paint with 1 \(\frac{3}{4}\) gallons of blue paint. How many gallons of purple paint did he make?
Number model: __________
Estimate: _________
__________ gallons
Answer:

Question 2.
Ethel had 4 feet of ribbon. She used 1 \(\frac{1}{4}\) feet for a craft project. How many feet of ribbon does she have left?
Number model: __________
Estimate: _________
__________ feet
Answer:

Question 3.
A macaroni and cheese recipe calls for 1\(\frac{2}{3}\) cups of shredded cheddar cheese and 1 \(\frac{2}{3}\) cups of shredded mozzarella cheese. How many cups of cheese are used in the recipe?
Number model: _________
Estimate: _________
_________ cups
Answer:

Practice
Divide. Show your work on the back of the page.
Question 4.
6,125 ÷ 44 = ?
Estimate: _________
Answer:

Question 5.
2,967 ÷ 21 = ?
Estimate: ___________
Answer:

Everyday Math Grade 5 Home Link 3.10 Answer Key

Fraction Addition with Circle Pieces
Question 1.
a. These fraction circle pieces show \(\frac{1}{3}\) + \(\frac{1}{6}\). Draw a line to show how you could use fraction circle pieces to change the problem to \(\frac{2}{6}\) + \(\frac{1}{6}\).

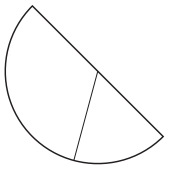
Answer:

b. Complete the number sentences.
\(\frac{2}{6}\) + \(\frac{1}{6}\) = __________
\(\frac{1}{3}\) + \(\frac{1}{6}\) = ____________
Answer:

Question 2.
a. What fraction addition problem do these fraction circles show? _________

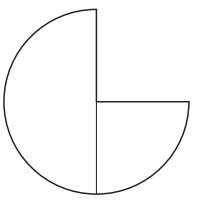
Answer:

b. Draw a line to show how you could use the fraction circle pieces above to change the problem so that both fractions have the same denominator.
Answer:

c. Complete the number sentences.

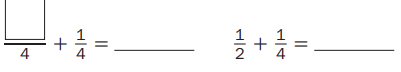
Answer:

Question 3.
Explain why it is easier to add fractions when they have the same denominator.
Answer:

Practice
Write an expression to model each situation.
Question 4.
Sandra picked 10 blue flowers and 16 red flowers. Then she divided the flowers equally into 2 bouquets. ____________
Answer:

Question 5.
A recipe called for \(\frac{2}{3}\) cup flour. Kyle doubled the recipe. Then he added \(\frac{1}{4}\) cup more flour to make the dough less sticky. ___________
Answer:

Everyday Mathematics Grade 5 Home Link 3.11 Answers

Playing Fraction Capture

Question 1.
Cole was playing Fraction Capture. He recorded his addition expressions, but he forgot to write down the fractions he formed with his dice rolls.
Fill in the fraction column of Cole’s record sheet with fractions he might have formed.

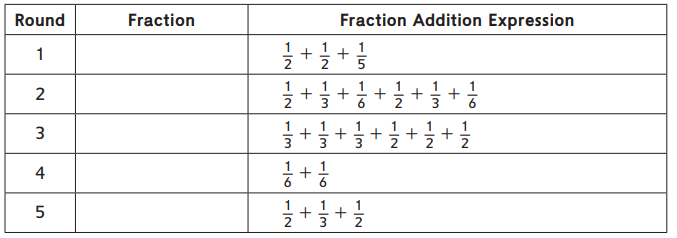
Answer:

Question 2.
Mackenzie was playing Fraction Capture and rolled a 6 and a 2.
a. Write an addition expression to show fractions she could have captured if she used her dice rolls to form \(\frac{2}{6}\).
Answer:

b. Write an addition expression to show fractions she could have captured if she used her dice rolls to form \(\frac{6}{2}\).
Answer:

Practice
Write each of the fractions below as a division expression. Then write each fraction as a whole number or a mixed number.
Question 3.
\(\frac{5}{4}\)
Division expression: _________
Mixed or whole number: _________
Answer:

Question 4.
\(\frac{16}{8}\)
Division expression: _________
Mixed or whole number: _________
Answer:

Question 5.
\(\frac{14}{3}\)
Division expression: _________
Mixed or whole number: _________
Answer:

Question 6.
\(\frac{17}{12}\)
Division expression: _________
Mixed or whole number: _________
Answer:

Everyday Math Grade 5 Home Link 3.12 Answer Key

Solving Fraction Number Stories

Solve each number story. Show your work and make sure your answer is clear.
Question 1.
Anton is training for a cross-country race. He ran 2 \(\frac{2}{4}\)miles on Saturday and 3 \(\frac{1}{4}\) miles on Sunday. How much farther did Anton run on Sunday? How do you know?
Answer:

Question 2.
Nina had 9 apples to share with 5 of her friends. If all 6 people get an equal share, how many apples will each person get? How do you know?
Answer:

Question 3.
Anna and Daniel are playing Fraction Capture. Anna is trying to find sections that add up to \(\frac{3}{4}\). She knows that \(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4}\), but she wants to earn an extra point for using a fraction with a different denominator. Write another number sentence Anna could use to show a sum of \(\frac{3}{4}\).
Answer:

Practice
Find the volume of each figure below.
Question 4.

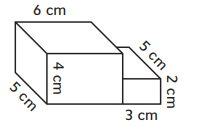
Volume = __________
Answer:

Question 5.

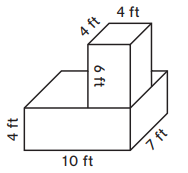
Volume = __________
Answer:

Everyday Math Grade 5 Home Link 3.13 Answer Key

Solving Fraction-Of Problems

Question 1.
What is \(\frac{1}{2}\) of 24?
Answer:

Question 2.
What is \(\frac{1}{3}\) of 24?
Answer:

Question 3.
What is \(\frac{1}{4}\) of 24?
Answer:

Question 4.
An animal shelter has 36 pets available for adoption. \(\frac{1}{4}\) of them are puppies. How many are puppies?
______________ of the pets are puppies.
Answer:

Question 5.
A teacher had 20 ounces of water in her water bottle. She drank \(\frac{1}{5}\) of the water. How many ounces did she drink?
She drank __________ ounces.
Answer:

Practice
Make an estimate. Then divide. Write your remainder as a fraction. Use your estimate to check the reasonableness of your answer.
Question 6.
7,002 ÷ 53 = ?
Estimate: ___________
Answer:

Question 7.
2,956 ÷ 67 = ?
Estimate: ___________
Answer:

Everyday Mathematics Grade 5 Home Link 3.14 Answers

Solving More Fraction-Of Problems

In today’s lesson you used drawings to solve fraction-of problems that do not have whole number answers. For example, you could find \(\frac{1}{2}\) of 7 by drawing:

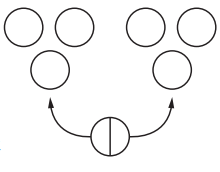
Today you used drawings to solve fraction-of problems that do not have whole number answers. For example, you could find \(\frac{1}{2}\) of 7 by making a drawing like the one at the right.
Question 1.
What is \(\frac{1}{2}\) of 7?
Answer:

Question 2.
What is \(\frac{1}{3}\) of 7?
Answer:

Question 3.
What is \(\frac{1}{4}\) of 7?
Answer:

Question 4.
Kai had 15 yards of kite string. He had to cut off \(\frac{1}{4}\) of it when his kite got stuck in a tree. How much string did he cut off?
He cut off ________ yards of string.
Answer:

Question 5.
Joan made 3 quarts of soup. She ate \(\frac{1}{7}\) of the soup each day for a week. How much soup did she eat each day?
She ate ________ quart of soup.
Answer:

Practice
Make an estimate. Then multiply. Use U.S. traditional multiplication for at least one problem. Use your estimate to check the reasonableness of your answer. Show your work on the back.
Question 6.
35 ∗ 49 = ?
Estimate: ____________
Answer:

Question 7.
209 ∗ 63 = ?
Estimate: ____________
Answer: