Everyday Math Grade 5 Answers Unit 6 Investigations in Measurement; Decimal Multiplication and Division

Everyday Mathematics 5th Grade Answer Key Unit 6 Investigations in Measurement; Decimal Multiplication and Division

Everyday Mathematics Grade 5 Home Link 6.1 Answers

Multiplying and Dividing by Powers of 10

Use the ideas below to help you solve Problems 1–9
To multiply by a power of 10, move the decimal point to the right of the number of places indicated by the exponent. For example, to multiply by 103, move the decimal point to the right 3 places. This works because the exponent tells the number of times a start number is multiplied by 10. Each time a number is multiplied by 10, the digits shift 1 place to the left, which moves the decimal point 1 place to the right.
Example: 4.3 × 10³ = 4.3 × 10 × 10 × 10 = 4,300

To divide by a power of 10, move the decimal point to the left of the number of places indicated by the exponent. For example, to divide by 103, move the decimal point to the left in 3 places. This works because dividing by 10 is the same as multiplying by \(\frac{1}{10}\). Each time a number is multiplied by \(\frac{1}{10}\), the digits shift from 1 place to the right, which moves the decimal point from 1 place to the left.
Example: 4.3 ÷ 10³ = 4.3 ÷ (10 × 10 × 10) = 4.3 ÷ 1,000 = 0.0043

Question 1.
6.8 × 10² = _________
Answer:

6.8 x (10 × 10) = 6.8×100 = 680

Question 2.
43.9 ÷ 10² = _________
Answer:

43.9 ÷ (10 × 10) = 43.9 ÷ 100 =0.439

Question 3.
237.5 ÷ 10² = _________
Answer:

237.5 ÷ (10 × 10) = 237.5 ÷ 100 = 2.375

Question 4.
5.29 × 10⁴ = _________
Answer:

5.29 x (10 x 10 x 10 x 10) = 5.29 x 10000 = 52900

Question 5.
13.2 ÷ 10³ = __________
Answer:

13.2 ÷ (10 × 10 × 10) = 13.2 ÷ 1,000 = 0.0132

Question 6.
71.8 × 10³ = _________
Answer:

71.8 x (10 x 10 x 10) = 71.8 x 1000 = 71800

Question 7.
9.4 × 10⁵ = _______
Answer:

9.4 x (10 x 10 x 10 x 10 x 10) = 9.4 x 100000 = 940000

Question 8.
3.6 ÷ 10⁴ = _________
Answer:

3.6 ÷ (10 × 10 × 10 x 10) = 3.6 ÷ 10000 = 0.00036

Question 9.
Explain how you moved the decimal point in Problem 2 and why. Use clear mathematical language.
Answer:

In problem 2, there is division. In the case of division, we should move the decimal point to the left side in the numerator concerning the number of zeroes in the denominator. There are two zeroes in problem 2, so we have to move two decimal points left side.

Practice
Question 10.

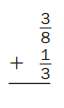
Answer:

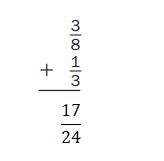
Question 11.

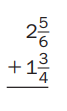
Answer:

 

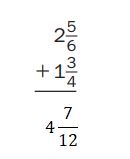
Everyday Math Grade 5 Home Link 6.2 Answer Key

Playing Exponent Ball

Tony is playing Exponent Ball. He wrote down each of his expressions but wasn’t sure how far to move the ball on each play.
Question 1.
Complete Tony’s record sheet. Use Table 1 to determine the number of yards to move the ball.

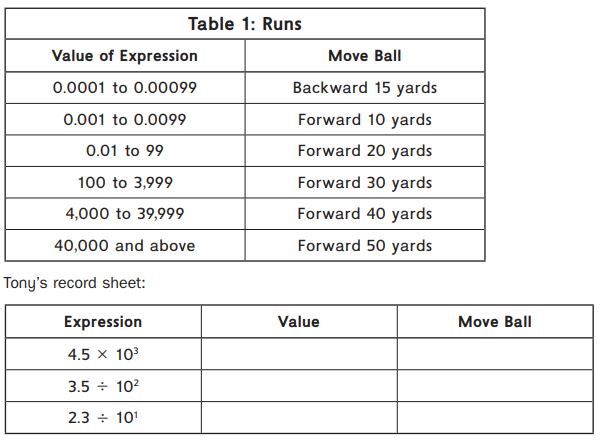
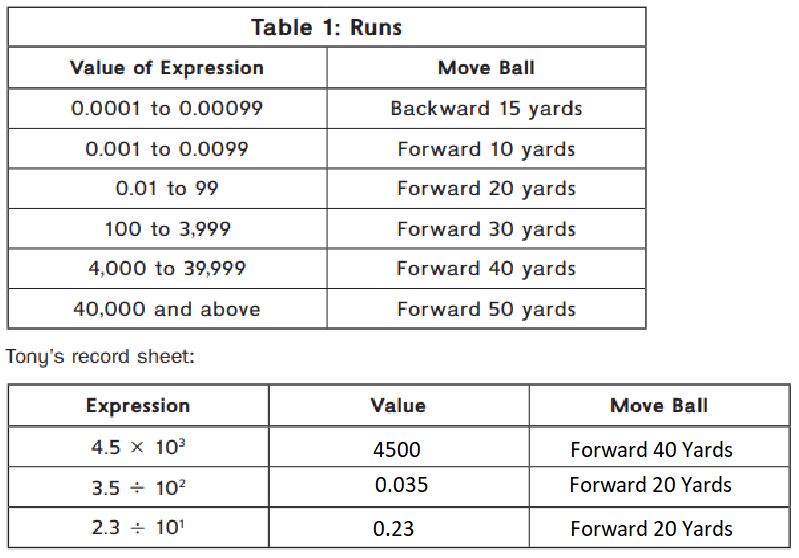
Answer:

 

Question 2.
Choose one of the expressions. Explain how you found the value and determined how far to move the ball.
Answer:

In the first expression, there is multiplication. So, we have to move the decimal to the right side. Hence, there are 3 zeroes, decimal is moved to right up to three values. And also with the help of the above table, 4500 lies between 4000 to 39,999. So, the ball should be Forwarded 40 Yards.

Practice
Question 3.

Answer:

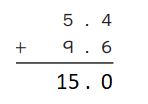
Question 4.

Answer:

Question 5.

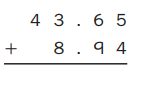
Answer:

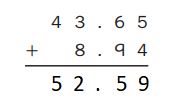
Everyday Mathematics Grade 5 Home Link 6.3 Answers

Solving Conversion Problems

Question 1.
Convert between kilograms (kg) and grams (g) to complete the table below.

Answer:

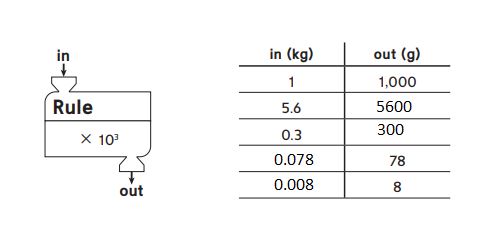
Question 2.
What rule could you use to convert from grams to kilograms? Hint: How can you find them in number if you know the outnumber? Use exponential notation.
Answer: 1000 grams is equal to 1kg i.e., (1 Kg = 10³ ).

Use the rules from Problems 1 and 2 to help you solve the number stories below. Show your work. Label the units for each step.
Question 3.
Micah has a cat and a parrot. Her cat weighs 2.3 kg and her parrot weighs 65 g. How many more kilograms does the cat weigh than the parrot?
The cat weighs _________ kg more than the parrot.
Answer:

The cat weighs 2.235 kg more than the parrot.

Question 4.
Jasmine’s dog weighs 15 kg. The dog’s collar weighs 200 g. How many grams does the dog weigh when it is wearing its collar?
The dog weighs _______ g with its collar.
Answer:

The dog weighs 14,800 g with its collar

Practice
Solve.
Question 5.

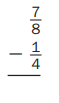
Answer:

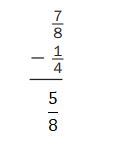
Question 6.

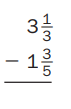
Answer:

 

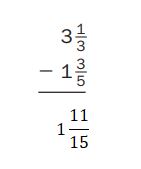
Everyday Math Grade 5 Home Link 6.4 Answer Key

Using Line Plots to Analyze Growth

Sammy and Marla are keeping track of how much they grow each month.
Question 1.
a. Use the information in the table to make a line plot to show Sammy’s growth.

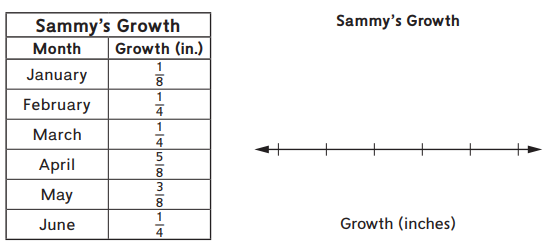
Answer:

 

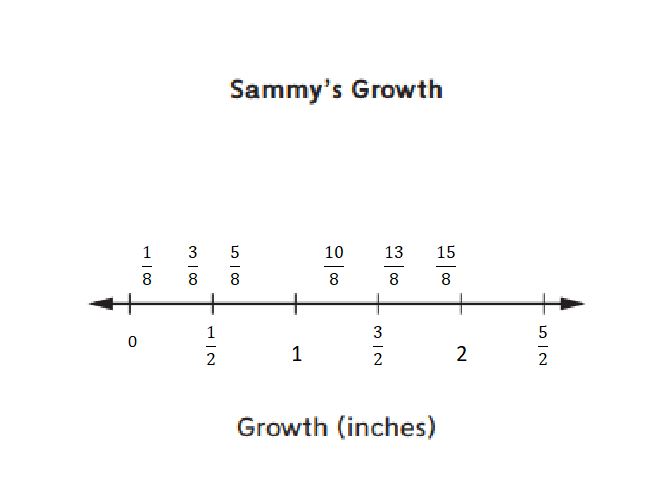
b. How much did Sammy grow in 6 months? ________ inches
Answer:

15/8 inches. 

Question 2.

a. Use the information in the table to make a line plot to show Marla’s growth.

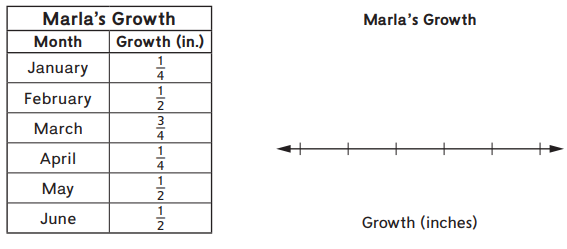
Answer:

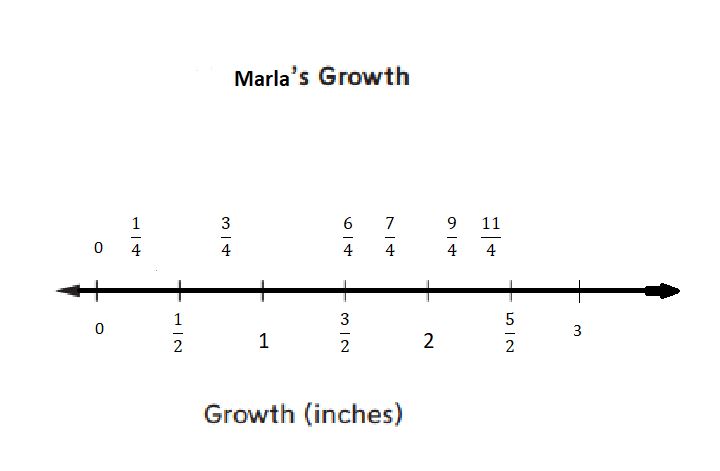
b. How much did Marla grow in 6 months? ________ inches
Answer:

11/4 inches

Question 3.
a. Who grew more in 6 months, Sammy or Marla?
b. How much more?
c. Write a number model to show how you solved Part b.
Answer:

a. Marla grew more in 6 months.

b. 7/8 inches more than Sammy

c. Marla’s Height = 11/4 = 22/8

Sammy’s Height = 15/8

Therefore, 22/8-15/8 = 7/8.

Everyday Mathematics Grade 5 Home Link 6.5 Answers

A Milkshake Problem

Rachel is having a slumber party with 7 friends. Her mom made a big batch of milkshakes. Rachel’s little brother tried to help by pouring the milkshakes in glasses, but he had trouble pouring the same amount into each glass

Question 1.
Plot the amount of milkshake in each glass on the line plot below.

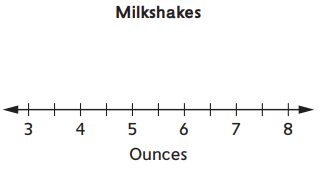
Answer:

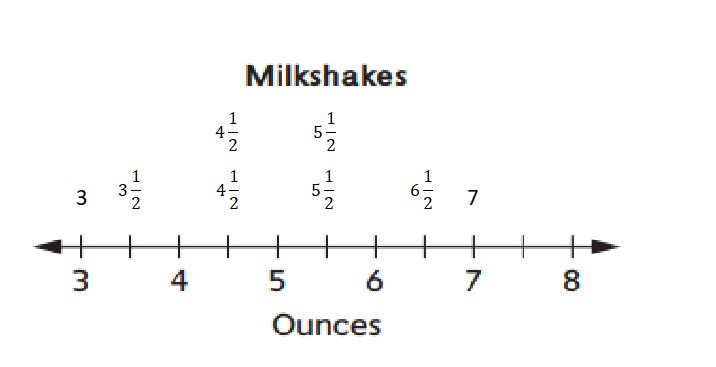
Rachel wants to even out the servings so that everyone will get the same amount of milkshakes. Answer the questions to help you figure out how many ounces Rachel should pour into each glass.

Remember: To even out data, add all the numbers in the data set, and then divide by the number of data points.
Question 2.
a. How many total ounces of milkshake did Rachel’s mom make? __________ ounces

Answer:

40 ounces of milkshakes
b. How many glasses of milkshake are needed? __________ glasses

Answer:

8 glasses are needed because there are a total of 8 members (1+7)

c. Write a number model that represents dividing the milkshake evenly among all the glasses. __________

Answer:

To divide the milkshake evenly among all the glasses,

Number of  ounces of milkshake / total members

i.e., 40 ounces / 8 members = 5

therefore, 5 ounces of milkshake should be poured into each glass for evenly distribution.

d. How many ounces of milkshake will each friend get? __________ ounces
Answer:

5 ounces of milkshake will each friend get

Practice
Solve.
Question 3.
7.6 × 10² = __________
Answer:

7.6 x (10 x 10) = 760

Question 4.
18.2 ÷ 10² = __________
Answer:

18.2 ÷ (10 x 10) = 0.182

Question 5.
779.5 ÷ 10⁴ = __________
Answer:

779.5 ÷ (10 x 10 x 10 x 10) = 0.7795

Question 6.
81.23 × 10⁴ = __________
Answer:

81.23 × (10 x 10 x 10 x 10) = 0.008123

Everyday Math Grade 5 Home Link 6.6 Answer Key

Using Volume Formulas

Formulas for Volume of a Rectangular Prism
V = l ∗ w ∗ h
V = B ∗ h

Use either of the volume formulas to help you solve the problems below. Write a number model to show how you found the volume. You may use a calculator.
Question 1.
The Aon Center in Chicago is a tall square tower. Its base covers an area of about 37,636 square feet. The building is about 1,136 feet tall. What is the volume of the Aon Center?
Volume: about _____________ cubic feet
Number model: _________________
Answer:

Volume: about 42,754,496 cubic feet
Number model:

37,636*1,136 = 42,754,496

Question 2.
The Great Wall of China is about 20 feet high and about 15 feet wide. What is the volume of a 1-mile section of the wall? (The whole wall is more than 5,000 miles long!)
Hint: 1 mile = 5,280 feet
Volume: about _____________ cubic feet
Number model: _____________
Answer:

Volume: about 1,584,000 cubic feet
Number model:  5,280*20*15 = 1,584,000

Question 3.
The Cathedral of Notre Dame in Paris, France covers an area of 4,800 square meters. The roof is about 43 meters high. What is the volume of the interior of the cathedral?
Volume: about _____________ cubic meters
Number model: _____________
Answer:

Volume: about 206,400 cubic meters
Number model:  4,800*43 =206,400

Practice
Multiply. Show your work.
Question 4.
\(\frac{2}{3}\) ∗ 34 = ________
Answer:

= 2/3 x 34

= 68/3

Question 5.
72 ∗ \(\frac{1}{7}\) = _________
Answer:

= 72 x 1/7

= 72/7

Everyday Mathematics Grade 5 Home Link 6.7 Answers

Volume in Milliliters and Cubic Centimeters

Solve the problems below. Use V = l × w × h and V = B × h to help you solve. Record the volumes in cubic centimeters and milliliters. Remember: 1 cm³ = 1 mL
Question 1.
The area of the base of a pencil case is 100 square centimeters. The pencil case is 5 centimeters tall. What is the volume of the pencil case?
_____________ cm³
_____________ mL
Answer:

The volume of the pencil case is 500 cm³

The volume of the pencil case is 500 mL

Question 2.
A small aquarium is 20 centimeters long and 25 centimeters wide. The water in the aquarium is 20 centimeters high. What is the volume of the water in the aquarium?
_____________ cm³
_____________ mL
Answer:

The volume of the water in the aquarium is 10,000 cm³

The volume of the water in the aquarium is 10,000 mL

Question 3.
Alex has a calibrated bottle. The water level is at the 0 mL mark. When Alex places a baseball under the water, the water level rises to the 200 mL mark. What is the volume of the baseball?
_____________ cm³
_____________ mL
Answer:

The volume of the baseball is 200 cm³

The volume of the baseball is 200 mL

Question 4.
For each problem above, which unit of volume makes more sense? Explain your answers.
a. Problem 1:
Answer:

Units of values vary but the value remained constant. Hence, both units of volumes are the same in expressing the value.

b. Problem 2:
Answer:

Units of values vary but the value remained constant. Hence, both units of volumes are the same in expressing the value.

c. Problem 3:
Answer:

Units of values vary but the value remained constant. Hence, both units of volumes are the same in expressing the value.

Practice
Multiply.
Question 5.
\(\frac{7}{8}\) ∗ \(\frac{1}{2}\) = _________
Answer:

= 7/8 x 1/2

= 7×1 / 8×2

= 7/16

Question 6.
\(\frac{5}{9}\) ∗ \(\frac{5}{6}\) = __________
Answer:

= 5/9 x 5/6

= 5×5 / 9×6

= 25/54

Everyday Math Grade 5 Home Link 6.8 Answer Key

Estimating Decimal Products and Quotients

Kyle and Emma came up with different answers to their homework. For each problem, make an estimate. Write a number sentence to show how you estimated. Then circle the student who has the correct answer.
Question 1.
8.82 ÷ 1.4 = ? Estimate: ___________
Kyle: 63
Emma: 6.3
Answer:

The estimated value is 6.3.

Because 1.4 x 6.3 nearly equals 8.82

Emma has the correct answer

 

Question 2.
17.6 ∗ 8.5 = ? Estimate: ___________
Kyle: 149.6
Emma: 14.96
Answer:

Estimated value is 149.6

Because when 17.6 x 8.5 equals to 149.6

Kyle has the correct answer

Question 3.
2,812.95 ÷ 89.3 = ? Estimate: ___________
Kyle: 31.5
Emma: 315.0
Answer:

Estimated value  is 31.5

Because, when 2,812.95 ÷ 89.3 equals to 31.5

Kyle has the correct answer

Question 4.
65.2 ∗ 112.5 = ? Estimate: ___________
Kyle: 733.5
Emma: 7,335
Answer:

Estimated value is 7,335

Because, when 65.2 x 112.5 equals 7,335

Emma has the correct answer

 

Question 5.
209.1 ÷ 24.6 = ? Estimate: ___________
Kyle: 8.5
Emma: 85.0
Answer:

Estimated value is 8.5

Because, When 24.6 x 8.5 equals 209.1

Kyle has the answer

Question 6.
3.6 ∗ 0.25 = ? Estimate: ___________
Kyle: 9.0
Emma: 0.9
Answer:

Estimated value is  0.9

Because, When 3.6 x 0.25  equals 0.9

Emma has the answer.

Practice
Make an estimate. Then solve.
Question 7.
526 ÷ 17 =?

Answer:

Question 8.
\(\frac{1963}{88}\) = ?

Answer:

Everyday Mathematics Grade 5 Home Link 6.9 Answers

Multiplying Decimals

Today you learned two different strategies for multiplying decimals. Try to use each decimal multiplication strategy at least once to solve Problems 1–4. Show your work on the back of this page.

Estimation Strategy
Make an estimate.
Multiply as if the factors were whole numbers.
Use your estimate to insert a decimal point in the product.
Example: 70.4 ∗ 18.6 = ?
Think: 70 ∗ 20 is about 1,400.
704 ∗ 186 = 130,944
The product should be close to 1,400, so it must be 1,309.44.

Shifting the Decimal Point Strategy
Multiply each factor by a power of 10 to get whole numbers.
Multiply the whole-number factors.
“Undo” the multiplication by powers of 10. Think about how dividing by the same powers of 10 would shift the decimal point in the answer.
Example: 70.4 ∗ 18.6 = ?
70.4 ∗ 101 = 704 18.6 ∗ 101 = 186
704 ∗ 186 = 130,944
Think: Dividing by 101 will shift the decimal point from 1 place to the left, and dividing by the other 101 will shift the decimal point to another place to the left.
I need to shift it to two places in all. So
70.4 ∗ 18.6 = 1,309.44.

Question 1.
81.3 ∗ 47.5 = ________
Answer:

= (81.3 x 10) * (47.5 x 10)

= (813) * (475)

= 3,86175

by move two decimal points to left side,

Therefore, 81.3 ∗ 47.5 = 3,861.75

Question 2.
7.8 ∗ 215.6 = __________
Answer:

Estimated value is 1,720

(7.8*10) * (215.6*10)

78 x 2156

168,168

Shifting the two decimal points to left side,

= 1681.68

The product should be close to 1,720, so it must be 1681.68

Question 3.
0.57 ∗ 3.0 = ________
Answer:

Estimated value is 1.5

(0.57*100) * (3*100)

57 x 300

17,100

Shifting the four decimal points to left side,

= 1.71

The product should be close to 1.5, so it must be 1.71

1.71

Question 4.
1,094.25 ∗ 22.6 = ___________
Answer:

Estimated value is 25,162

(1,094.25*100) * (22.6*100)

109425 *2260

247300500

Shifting the four decimal points to left side,

= 24730.05

The product should be close to 25,162 , so it must be 24,730.

Practice
Solve. Show your work on the back of this page.
Question 5.
\(\frac{1}{9}\) ÷ 5 = _______
Answer:

= 1/9 ÷ 5

= 1/ (9 x 5)

= 1/45

Question 6.
\(\frac{1}{2}\) ÷ 12 = _______
Answer:

= 1/2 ÷ 12

= 1/ (2 x 12)

= 1/24

Everyday Math Grade 5 Home Link 6.10 Answer Key

Checking Whether My Answer Makes Sense

Question 1.
Pizza by the Pan sold 4 dozen pizzas in the afternoon. That night, they sold 2.5 times as many pizzas as they did during the afternoon. How many pizzas did they sell in all that day? Show your work and check whether your answer makes sense. Show how you can tell that your answer makes sense.
Answer:

Number of pizzas sold in the afternoon = 4 dozens = 4 x 12 = 48

Number of pizzas sold in the night = 2.5 times the pizzas sold in the afternoon = 2.5 x 48 = 120

Therefore, Total number of pizzas sold in a day is 48 + 120 =168.

Practice
Divide. Show your work on the back of this page.
Question 2.
6 ÷ \(\frac{1}{3}\) = _________
Answer:

= 6 ÷ 1/3

= (6 x 3) /1

= 18

Question 3.
10 ÷ \(\frac{1}{4}\) = __________
Answer:

= 10 ÷ 1/4

= (10 x 4) /1

= 40

Everyday Mathematics Grade 5 Home Link 6.11 Answers

Dividing Decimals by Whole Numbers

For Problems 1 and 2:

• Make an estimate. Write a number sentence to record your estimate.
• Divide as if the dividend were a whole number. Show your work on the computation grid.
• Use your estimate to place the decimal point. Record your answer.

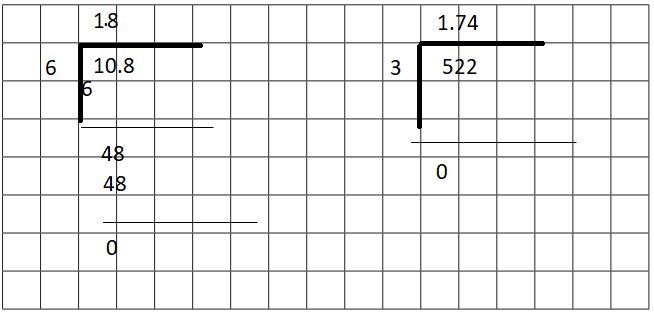
Question 1.
\(\frac{10.8}{6}\) = ?
Estimate: _________

\(\frac{10.8}{6}\) = _________
Answer:

Estimate : 1.67

= (10.8*10) / (6)

108/6

18.0

By shifting the one decimal point to the left side, it is 1.8

It is very close to 1.67. Then it must be 1.8

Question 2.
\(\frac{5.22}{3}\) = ?
Estimate: _________

\(\frac{5.22}{3}\) = _________
Answer:

Estimate : 1.66

= (5.22*100) / (3)

522/3

174.0

By shifting the two decimal points to the left side, it is 1.74

It is very close to 1.66. Then it must be 1.74

Answer:

Practice
Multiply. Show your work.
Question 3.
\(\frac{2}{5}\) ∗ 30 = _______
Answer:

= 2/5 * 30

= 2*30 /5

= 60/5 =12

Question 4.
16 ∗ \(\frac{1}{3}\) = ________
Answer:

= 16*1 /3

= 16/3

Everyday Math Grade 5 Home Link 6.12 Answer Key

Dividing by Decimals

For Problems 1–3:

• Rewrite the problem as an equivalent problem that has a whole-number divisor. Be sure to multiply the dividend and divisor by the same number.
• Solve the equivalent problem using any method you wish. If you don’t solve the problem mentally, show your work.
• Record your answer to the equivalent problem and the original problem.

One example is done for you.

Example: 2.8 ÷ 0.4 = ?
Think: Multiplying 0.4 by 10 will give me a whole number, so I should also multiply 2.8 by 10 to make an equivalent problem.
(2.8 ∗ 10) ÷ (0.4 ∗ 10) = 28 ÷ 4
Equivalent problem: 28 ÷ 4 = ?
Answer to equivalent problem: 7
2.8 ÷ 0.4 = 7

Question 1.
7.2 ÷ 0.6 = ?
Equivalent problem: ___________
Answer to equivalent problem: ___________
7.2 ÷ 0.6 = ___________
Answer:

(7.2 * 10) ÷ (0.6 ∗ 10) = 72 ÷ 6

Equivalent problem:  72 ÷ 6

Answer to equivalent problem: 12

7.2 ÷ 0.6 = 12

Question 2.
44 ÷ 0.5 = ?
Equivalent problem: ___________
Answer to equivalent problem: ___________
44 ÷ 0.5 = ___________
Answer:

(44 * 10) ÷ (5) = 440÷5

Equivalent problem:  440 ÷ 5

Answer to equivalent problem: 88

44 ÷ 0.5 = 88

Question 3.
1.92 ÷ 0.16 = ?
Equivalent problem: ___________
Answer to equivalent problem: ___________
1.92 ÷ 0.16 = ___________
Answer:

(1.92 * 100) ÷ (0.16 * 100) = 192÷16

Equivalent problem:  192 ÷ 16

Answer to equivalent problem: 12

1.92 ÷ 0.16 = 12

 

Practice
Add. Show your work on the back of this page.
Question 4.
6.48 + 9.34 = ___________
Estimate: ___________
Answer:

Estimate = 15.8

Answer = 15.82

Question 5.
15.71 + 12.2 = ___________
Estimate: ___________
Answer:

Estimate = 28

Answer = 27.91

Everyday Mathematics Grade 5 Home Link 6.13 Answers

Interpreting Reaction-Time Data

Garrett tried the Grab-It Gauge experiment with his left hand. He recorded his results on the line plot below. Use the data to answer the questions.

Question 1.
Which time(s) came up most often for Garrett? ___________ sec
Answer:

0.15,0.16,0.17,0.18 (each two times) came up most often for Garrett

Question 2.
Write Garrett’s reaction times in order from fastest to slowest.
Answer:

0.19, 0.18, 0.18, 0.17, 0.17, 0.16, 0.16, 0.15, 0.15, 0.14  are reaction times from fastest to lowest.

Question 3.
What is the difference between Garrett’s fastest time and his slowest time?
___________ sec
Answer:

Fastest time = 0.19 secs

Slowest time = 0.14 secs

Difference = 0.19-0.14 = 0.05

Therefore, the difference between Garrett’s fastest time and his slowest time is 0.05 secs.

Question 4.
What is Garrett’s evened-out reaction time? Record your calculations.
Expression: ___________
Evened-out reaction time: ___________ sec
Answer:

Question 5.
What would you say is a typical reaction time for Garrett’s left hand? Why?
Answer:

0.165 is is a typical reaction time for Garrett’s left hand because it is mean for the given reaction times.

Practice
Subtract. Show your work on the back of this page.
Question 6.
5.63 – 2.19 = ___________
Estimate: ___________
Answer:

Estimate = 3.5

Answer = 3.44

Question 7.
44.12 – 3.85 = ___________
Estimate: ___________
Answer:

Eestimate = 40

Answer = 40.27