Everyday Math Grade 3 Answers Unit 3 Operations

Everyday Mathematics 3rd Grade Answer Key Unit 3 Operations

Everyday Mathematics Grade 3 Home Link 3.1 Answers

“ What’s My Rule? ”

Family Note Today your child practiced adding, subtracting, multiplying, and dividing in “What’s My Rule?” problems. Children were introduced to the “What’s My Rule?” routine in Kindergarten Everyday Mathematics. In First and Second Grade Everyday Mathematics, they continued to use the routine to practice addition and subtraction. You can find an explanation of function machines and “What’s My Rule?” tables on pages 74-75 in the Student Reference Book. Ask your child to explain how they work. Help your child fill in all the missing parts for these problems.

Complete the “What’s My Rule?”problems. Make up problems of your own for the last table. Explain to someone how you figured out the in and out numbers.
Question 1.

Answer:

Explanation:
Rule : Subtract 7 so
in – 14 , out – 14 -7 = 7,
in -7, out – 7 – 0 = 7,
in – 12, out – 12 – 7 = 5,
in – 15, out – 15 – 7 = 8,
in – 10, out – 10 – 7 = 3,
in – 21, out – 21 – 7 = 14 as shown above.

Question 2.

Answer:

Explanation:
Rule : Multiply by 5 so
in – 1 , out – 1 X 5 = 5,
in -5, out – 5 X 5 = 25, (25/5 = 5),
in – 4, out – 4 X 5 = 20,(20/5 = 4),
in – 6, out – 6 X 5 = 30, (30/5 = 6),
in – 2, out – 2 X 5 = 10 as shown above.

Question 3.

Answer:

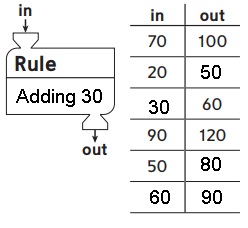
Explanation:
Rule : Adding 30 so
in – 70 , out – 70 + 30 = 100,
in -20, out – 20 + 30 = 50,
in – 30, out – 30 + 30 = 60, (60 – 30 = 30),
in – 90, out – 90 + 30 = 120,
in – 50, out – 50 + 30= 80,
in – 60, out – 60 + 30 = 90, (90 – 30 = 60)  as shown above.

Question 4.

Answer:

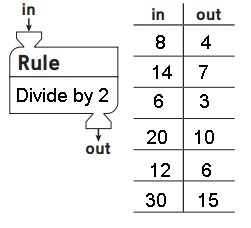
Explanation:
Rule : Dividing by 2 so
in – 8 , out – 8/2 = 4,
in -6, out – 6/2 = 3,
in – 20, out – 20/2 = 10,
in – 12, out – 12/2 = 6,
in – 30, out – 30/2= 15 as shown above.

Everyday Math Grade 3 Home Link 3.2 Answer Key

Solving Problems Home Link 3-2 with Estimation

Family Note Today your child used close-but-easier numbers and estimation to solve problems. Ask your child to explain what a close-but-easier number is and when it might make sense to use an estimate rather than an exact answer. Using mental math in making estimates is important in everyday life and in Everyday Mathematics.

Question 1.
Use close-but-easier numbers to estimate the answer to this problem.
78 + 43 = ?
My close-but-easier numbers are _____120________
My estimate is ___121_______
Answer:
My close-but-easier numbers are 120,
My estimate is 121,

Explanation:
Used close-but-easier numbers to estimate
the answer to this problem 78 + 43 =
My close-but-easier numbers are 120,
My estimate is 121.

Question 2.
At their October meeting, the school’s book club set a goal for its members to read 1,000 books before the end of the year. In October the book club read 221 books, and in November they read 387 books. Without using a pencil and paper, use close-but-easier numbers to make an estimate of about how many books the club will need to read in December to reach its goal.
My close-but-easier numbers are _____400________.
The club needs to read about _____392________ books in December.
Answer:
My close-but-easier numbers are _____400________.
The club needs to read about _______392______ books in December,

Explanation:
Given at their October meeting, the school’s book club
set a goal for its members to read 1,000 books before
the end of the year.
In October the book club read 221 books, and in
November they read 387 books. Without using
a pencil and paper, used close-but-easier numbers
to make an estimate of about how many books the
club will need to read in December to reach its goal
as (1,000 – (221 + 387)) = 1,000 – 608 = 392 books,
Therefore, my close-but-easier numbers are 400.
The club needs to read about 392 books in December.

Everyday Mathematics Grade 3 Home Link 3.3 Answers

Partial-Sums Addition

Family Note Today your child learned about adding 3-digit numbers using partial-sums addition. Your child may choose to use partial-sums addition or may prefer a different method.

Solve each addition problem. You may want to use partial-sums addition. Use an estimate to check that your answer makes sense. Write a number model to show your estimate
Question 1.
Estimate: ____340_____

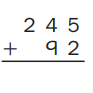
Answer:

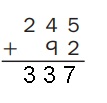
Explanation:
Solvedaddition problem used partial-sums addition.
Used an estimate to check that myour answer makes sense.
Wrote a number model to show my estimate as 340.

Question 2.
Estimate: _340________

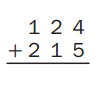
Answer:

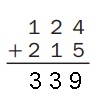
Explanation:
Solvedaddition problem used partial-sums addition.
Used an estimate to check that myour answer makes sense.
Wrote a number model to show my estimate as 340.

Question 3.
Estimate: __560_______

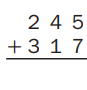
Answer:

Explanation:
Solvedaddition problem used partial-sums addition.
Used an estimate to check that myour answer makes sense.
Wrote a number model to show my estimate as 560.

Question 4.
Estimate: __570_______

Answer:

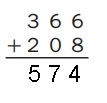
Explanation:
Solvedaddition problem used partial-sums addition.
Used an estimate to check that myour answer makes sense.
Wrote a number model to show my estimate as 570.

Everyday Math Grade 3 Home Link 3.4 Answer Key

Multidigit Addition

Family Note Today your child learned column addition, a strategy for adding multidigit numbers. Discuss the example with your child.

Tell someone about column addition.
Example: 248 + 79 = ?
Estimate: 200 + 100 = 300

Add each column of numbers.
There are two digits in the ones column, so trade 10 ones for 1 ten,
then move 1 ten to the tens column.
There are two digits in the tens column, 2 12 7 so trade 10 tens for 1 hundred, then move 1 hundred to the hundreds column.
248 + 79 = 327.

Question 1.
For the problem below, estimate the sum. Then use column addition to solve. Show your work. Use your estimate to check whether your answer makes
sense.
89 + 26 = ?
Estimate: _____90 + 30 = 120______
89 + 26 = _____115______
Answer:

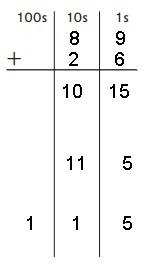
Explanation:
Adding each column of numbers.
There are two digits in the ones column,
so trade 10 ones for 1 ten,
then move 1 ten to the tens column.
There are two digits in the tens column,
1 1 so trade 10 tens for 1 hundred, then
move 1 hundred to the hundreds column.
89 + 26 = 115.

Everyday Mathematics Grade 3 Home Link 3.5 Answers

Counting-Up Subtraction

Family Note Today your child reviewed the counting-up method for subtraction. Discuss the example problem with your child.

Explain counting-up subtraction to someone at home. Use it to solve Problems 1 and 2. Show what you did on an open number line or with number sentences. Compare your answers to your estimates to check whether your answers make sense.
Example: 468 – 274 = ?
Estimate: 500 – 300 = 200

468 – 274 = 194

Question 1.
531 – 329 = ?
Estimate: ___500 – 300 = 200________
531 – 329 = ____202_______
Answer:

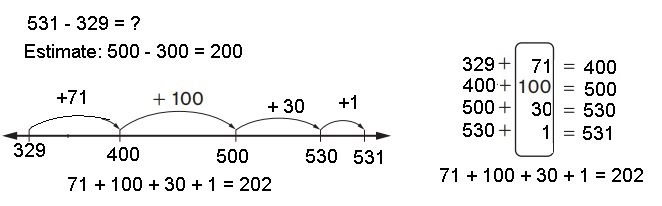
531 – 329 = 202,

Explanation:
Given to solve 531 – 329 =
So estimate is 500 – 200 = 200 and on number line
as shown above we get 531 – 329 = 202 which is near
to my estimate as 500 – 300 = 200, So 202 ≈ 200.

Question 2.
331 – 209 = ?
Estimate: __300 –  200 = 100___
331 – 209 = ____122_____
Answer:

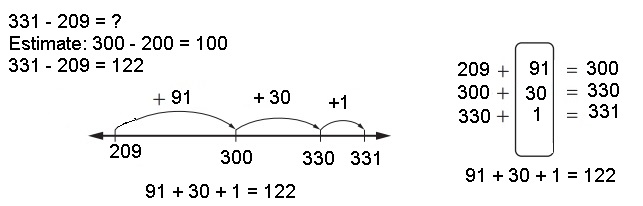
Explanation:
Given to solve 331 – 209 =
So estimate is 300 – 200 = 100 and on number line
as shown above we get 331 – 209 = 122 which is near
to my estimate as 300 – 200 = 100, So  122 ≈ 100.

Everyday Math Grade 3 Home Link 3.6 Answer Key

Expand-and-Trade Subtraction

Family Note Today your child used expand-and-trade subtraction to find differences between 3-digit numbers. This method reinforces children’s understanding of place value. Learning different strategies helps children think flexibly and apply strategies that make sense to them.

Fill in the unit. Estimate and then solve the problems. You may use any strategy you like. Use your estimates to check that your answers make sense. On the back of this Home Link, explain how you solved one of the problems.
Question 1.
Estimate: ____500 – 300 = 200___

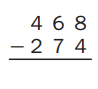
Answer:
Estimate : 500 – 300 = 200,

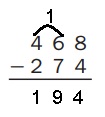
Explanation:
Given to solve 468 – 274,
As per estimate it is 500 – 300 = 200 and
solving we get 468 – 274 = 194, So 200 ≈ 194.

Question 2.
Estimate: ___500 – 300 = 200____

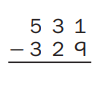
Answer:
Estimate : 500 – 300 = 200,

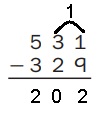
Explanation:
Given to solve 531 – 329,
As per estimate it is 500 – 300 = 200 and
solving we get 531 – 329 = 202, So 200 ≈ 202.

Question 3.
Estimate: ____300 – 200 = 100___

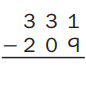
Answer:
Estimate : 300 – 200 = 100,

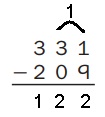
Explanation:
Given to solve 331 – 209,
As per estimate it is 300 – 200 = 100 and
solving we get 331 – 209 = 122, So 100 ≈ 122.

Question 4.
Estimate: ___600 – 400 = 200___

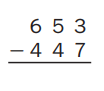
Answer:
Estimate :  600 – 400 = 200,

Explanation:
Given to solve 653 – 447,
As per estimate it is 600 – 400 = 200 and
solving we get 653 – 447 = 206, So 200 ≈ 206.

Everyday Mathematics Grade 3 Home Link 3.7 Answers

Scaled Bar Graph

Family Note Today your child sorted pattern blocks and created a bar graph with a scale of more than 1 to represent the data. Scales on bar graphs should have equally spaced intervals to represent data, such as below, where the scale is marked in intervals of 2.

Talk to someone at home about the data shown on the bar graph below. Then use the information shown on the graph to answer the questions.

Question 1.
How many more children chose Shuffle to 100 than Multiplication Draw?
Answer:
2 more children chose Shuffle to 100 than Multiplication Draw,

Explanation:
As per data shown on the bar graph above
Shuffle to 100 have 9 number of children and
Multiplication Draw have 7 number of children so
number of  more children chose Shuffle to 100 than
Multiplication Draw is 9 – 7 = 2.

Question 2.
How many more children chose Roll to 1,000 than Spin and Round?
Answer:
2 more children chose Roll to 1,000 than Spin and Round,

Explanation:
As per data shown on the bar graph above
Roll to 1000 have 6 number of children and
Spin and Round have 4 number of children
More children chose Roll to 1,000 than Spin and Round is
6 – 4 = 2,

Question 3.
How many fewer children chose Shuffle to 100 than the
combined total of children who chose Roll to 1,000 and
Multiplication Draw?
Answer:
4 fewer children chose Shuffle to 100 than the
combined total of children who chose Roll to 1,000 and
Multiplication Draw,

Explanation:
As per data shown on the bar graph above
Shuffle to 100 have 9 children, Roll to 1,000
have 6 children and Multiplication Draw have
7 children, So combined total of children who
chose Roll to 1,000 and Multiplication Draw are
6 + 7 = 13, Now fewer children chose Shuffle to 100
than the combined total of children who chose Roll
to 1,000 and Multiplication Draw are 13 – 9 = 4.

Question 4.
Write your own question about the graph. Then write the answer.
Answer:
The graph is about favourite math games,

Explanation:
On X-axis we have games names as Spin and Round,
Shuffle to 100, Multiplication Draw and Roll to 1,000
and on Y-axis we have number of children
from zero(0) to ten(10) as shown above.

Everyday Math Grade 3 Home Link 3.8 Answer Key

Interpreting a Picture Graph

Family Note Today your child learned to read and draw picture graphs with a scale of more than one. The key on a picture graph shows a symbol that represents the scale.

The picture graph shows how many fish each child caught on a fishing trip.

Use the graph to answer the questions.
Question 1.
How many fish did Amy catch? ____2____ fish
Answer:
2 fish Amy catch,

Explanation:
As shown in the picture graph Amy catch 2 fish,

Question 2.
How many fish did Chen catch? ___8_____ fish
Answer:
Chen catch 8 fish,

Explanation:
As shown in the picture graph Chen catch 8 fish,

Question 3.
How many more fish did Bill catch than Maria? ____6____ fish
Answer:
Bill catch 6 fish more than Maria,

Explanation:
As shown in the picture graph Bill catch 10 fish and
Maria has catched 4 fish, So more fish did Bill catch
than Maria is 10 – 4 = 6 fish.

Question 4.
Maria catches 3 more fish. Now how many has she caught in all? ____7____ fish
Answer:
Maria catches 7 fish in all,

Explanation:
As shown in the picture graph Maria has catch 4 fish,
if Maria catches 3 more fish then in all Maria catches
4 + 3 = 7 fish.

Revise the picture graph to show the number of fish Maria caught in all.
Question 5.
Did Chen and Max or Beth and Bill catch more fish? How many more? Explain your answer.
Answer:
Beth and Bill caught more fish than Chen and Max,
Beth and Bill caught 6 more fish,

Explanation:
As shown in the picture graph Beth catch
11 fish, Bill catch 10 fish so Beth and Bill caught
11 + 10 = 21 fish, Now Chen catch 8 fish and
Max catch 7 fish so Chen and Max catch 8 + 7 = 15 fish,
So more fish are catched by Beth and Bill than by
Chen and Max by 21 – 15 = 6 more fish.

Everyday Mathematics Grade 3 Home Link 3.9 Answers

Multiplication Squares

Family Note Today your child learned about multiplication squares,
such as 3 × 3 = 9 and 7 × 7 = 49.
Help your child practice multiplication squares by
completing the Rolling and Recording Squares activity below.
If you don’t have a 10-sided die, you will need a
set of cards numbered 1 through 10,
preferably two or more of each.
You can use a regular deck of playing cards 2–10,
using the aces as 1s.
Continue to help your child practice multiplication
with the included Fact Triangles.

Rolling and Recording Square s
Directions
1 Work with a family member.
2 Roll a 10-sided die (or draw a card) and make a
multiplication square using that number as both factors.
3 Figure out the product. Shade the first open box above that product.
4 Take turns until one column is filled. (If drawing cards, reuse them.)

Practice
Fill in the unit box. Write these problems on the back of this page and
show your work there. Write a number sentence for your estimate.
Use any method you wish to solve each problem.

1² = 1, Number sentence : 1 X 1 = 1,
2² = 4, Number sentence : 2 X 2 = 4,
3² = 9, Number sentence : 3 X 3 = 9,
4² = 16, Number sentence : 4 X 4 = 16,
5² = 25, Number sentence : 5 X 5 = 25,
6² = 36, Number sentence : 6 X 6 = 36,
7² = 49, Number sentence : 7 X 7 = 49,
8² = 64, Number sentence : 8 X 8 = 64,
9² = 81, Number sentence : 9 X 9 = 81,
10² = 100, Number sentence : 10 X 10 = 100.

Question 5.
Estimate: ___50 + 770 = 820_____
49 + 768 = ___817_____
Answer:
Estimate: 50 + 770 = 820,
49 + 768 = 817,

Explanation:
Given to solve 49 + 768 =,
Estimate is 50 + 770 = 820 and
49 + 768 = 817.

Question 6.
Estimate: ____360 + 600  = 960______
356 + 598 = ____954______
Answer:
Estimate: 360 + 600 = 960,
356 + 598 = 954,

Explanation:
Given to solve 356 + 598 =,
Estimate is 360 + 600 = 960 and
356 + 598 = 954.

×, ÷ Fact
Triangles: Multiplication Squares

Explanation:
As shown above in the triangle : Multiplication Squares
3 X 3 = 9, 9 ÷ 3 = 3,
4 X 4 = 16, 16 ÷ 4 = 4,
6 X 6 = 36, 36 ÷ 6 = 6,
7 X 7 = 49, 49 ÷ 7 = 7,
8 X 8 = 64, 64 ÷ 8 = 8,
9 X 9 = 81, 81 ÷ 9 = 9.

Everyday Math Grade 3 Home Link 3.10 Answer Key

The Turn-Around Rule for Multiplication

Family Note Today your child explored the turn-around rule for multiplication, which says two numbers may be multiplied in either order and the product will remain the same.
For example: 2 × 5 = 10 and 5 × 2 = 10.
Knowing this rule can help children multiply more easily.
Children also took inventory of the facts they can solve quickly and
easily and those they still need to practice.

Sketch an array to match each fact. Then sketch that array turned around. Record a number sentence to match the second array.
Question 1.

Answer:
Explanation:
Sketched an array to match each fact as 2 X 6 = 12,
Then sketched that array turned around as 6 X 2 = 12.
Recorded a number sentence to match the second array as
6 X 2 = 12 as shown above.

Question 2.

Answer:

Explanation:
Sketched an array to match each fact as 5 X 3 = 15,
Then sketched that array turned around as 3 X 5 = 15.
Recorded a number sentence to match the second array as
3 X 5 = 15 as shown above.

Question 3.
Use Problems 1 and 2 to tell someone why the turn-around rule works.
Answer:
The turn-around rule works and gets the same results,

Explanation:
Each array shows the same number of dots,
but the rows and columns are switched,
I can also switch the numbers around when I multiply
so the turn-around rule works and gets the same results.

Question 4.
Choose a multiplication fact you need to practice.
Write a strategy you can use to figure it out.
My fact: ______2____ × _____3_____ = ____6______
Strategy: ___3 + 3 = 6_______
Answer:
My fact : 3 X 2 = 6,
Strategy = 3 + 3 = 6,

Explanation:
My fact is 3 X 2 = 6 and applying strategy is
the repeated addition of the same number is
expressed by multiplication in short, hence
repeated addition of 3 two times is equal to
3 multiplied by 2, So 3 x 2 = 3 + 3 = 6, the result is same.

Everyday Mathematics Grade 3 Home Link 3.11 Answers

Adding a Group

Family Note Today your child learned another strategy for solving multiplication facts. Children used familiar facts, or helper facts, including the 2s, 5s, and 10s facts, to figure out facts they didn’t know. Today your child learned the adding-a-group strategy. Children added a group to helper 2s and 5s facts to solve other facts. Eventually children will know all their multiplication facts, but in the meantime, practicing strategies such as adding a group helps them figure out facts they do not know and also supports their understanding of multiplication and its properties.

Solve.
Question 1.
Jamila has 5 shelves of books with 7 books on each shelf.
How many books does she have?
Draw an array to show Jamila’s books.
5 × 7 = _____35_____
Answer:

Explanation:
Given Jamila has 5 shelves of books with
7 books on each shelf, So number of books
does she have are 5 X 7 = 35,
Drawn an array to show Jamila’s books above.

Question 2.
Jamila’s sister gives her 7 more books to fill a new shelf.
Now she has 6 rows of 7 books. Add a row of books to
your array above. Then figure out how many books Jamila has now.
6 × 7 = ____42____
Answer:

Explanation:
Given Jamila’s sister gives her 7 more books to fill a new shelf.
Now she has 6 rows of 7 books. Added a row of books to
my array above. Number of books Jamila has now are
6 X 7 = 42 books.

Question 3.
How did 5 × 7 help you figure out 6 × 7?
Answer:
5 X 7 helped to figure out 6 X 7 by adding
1 X 7 one more time to result of 5 X 7,

Explanation:
5 X 7 helped to figure out 6 X 7 as we get
5 X 7 = 35 to this result we add one more time 1 X 7
and get results of 6 X 7= 35 + 7 = 42,
therefore 5 X 7 helped to figure out 6 X 7.

Everyday Math Grade 3 Home Link 3.12 Answer Key

Subtracting a Group

Family Note Today your child learned the subtracting-a-group
strategy for solving multiplication facts.
Children subtracted groups from 5s and 10s helper facts
to solve other facts.
For example, to solve 4 × 6,
they might start with 5 × 6 = 30 and
subtract a group of 6: 30 – 6 = 24, so 4 × 6 = 24.
Continue to help your child practice multiplication
with the included Fact Triangles.

Question 1.
Use 10 × 4 and the array below to help figure out 9 × 4.
9 × 4 = ?
Helper fact: 10 × 4 = 40

a. Draw on the array above to show how to use
10 × 4 to figure out 9 × 4.
Answer:

Explanation:
Drawn on the array above to show how to use
10 × 4 to figure out 9 × 4 respectively.

b. Solve. 9 × 4 = ____36______
Answer:
9 X 4 = 36,

Explanation:
Solved 9 X 4 as 9 times 4 we get 36.

c. How did knowing 10 × 4 help you figure out 9 × 4?
Answer:
By subtracting 1 from 10 = 9 and multiplying with 4,
or as 10 X 4 = 40 and subtracting 1 group of 4 as
40 – 4 = 36,

Explanation:
10 X 4 helped out to figure out 9 X 4 by
subtracting 1 from 10 = 9 and then multiplying it
with 4 helped to solve 9 X 4 or multiplying 10 to 4
we get 40 to it subtracting 1 group of 4 we get
40 – 4 = 36 also.

Practice
Question 2.
9 × 10 =
Answer:
9 X 10 = 90,

Explanation:
To solve 9 X 10 we multiply 9 by 10 we get 90.

Question 3.
9 × 5 =
Answer:
9 X 5 = 45,

Explanation:
To solve 9 X 5 we multiply 9 by 5 we get 45.

Question 4.
__________ = 8 × 5
Answer:
40 = 8 X 5,

Explanation:
To solve 8 X 5 we multiply 8 by 5 we get 40.

Question 5.
____80______ = 8 × 10
Answer:
80 = 8 X 10,

Explanation:
To solve 8 X 10 we multiply 8 by 10 we get 80.

Everyday Mathematics Grade 3 Home Link 3.13 Answers

Name-Collection Boxes

Family Note Today your child discussed and wrote equivalent names for numbers in name collection boxes. You can find an explanation of name-collection boxes on pages 96-97 in the Student Reference Book.

Question 1.
Write at least 10 names for the number 18 in the name-collection box.
Then explain to someone at home how the box works.
Have that person add another name for 18.

Answer:

Explanation:
Wrote at least 10 names for the number 18 in the
name-collection box above as
1. 9 + 9, adding 9 to 9 we get 18,
2. 2 X 9, multiplying 2 by 9 we get 18,
3. Number of days in 2 weeks + 4 days means
14 + 4 = 18,
4. 36 ÷ 2 =18, Dividing 36 by 2 we get 18,
5. One and half dozen means 12 + 6 = 18,
6. By using tally numbers as shown above,
7. Adding 6 to 6 and 6 we get 18,
8. Subtracting 2 from 20 we get 18,
9. Writing 18 in words as Eighteen,
10. Adding 8 to 10 we get 18,
Now adding one more name for 18 as
multiplying 3 with 6 we get 18.

Question 2.
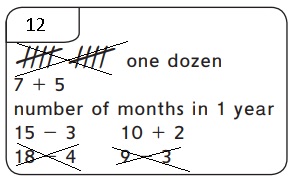
Three of the names do not belong in this box. Cross them out.
Then write the name of the box on the tag.

Answer:

Explanation:
Wrote three of the names do not belong in this box as
1. Tally number,
2. 18 – 4,
3. 9 – 3 crossed them out as shown above,
rest all names are 12 so wrote the name of
the box on the tag as 12.

Question 3.
Make up a problem like Problem 2. Do not write
the name of the box on the tag. Write 4 names for
the number and 2 names that are not names for the number.
To check whether the problem makes sense, ask someone
at home to tell you which 2 names do not belong.
Then have that person write the name of the box on the tag.
Answer:
Names are 1. 10 + 6,  2. 4 X 4,
3. 2 dozen,  4. 32 ÷ 2, 5. 24 – 4 and 6. 8 + 8,
Now 2 names that are not names for the number are
2 dozen and 24 -4, The name of the box on the tag is 16,

Explanation:
Wrote 4 names for the number and 2 names that
are not names for the number as
1. 10 + 6, adding 6 to 10 we get 16,
2. 4 X 4, multipling 4 by 4 we get 16,
3. 2 dozen,  two dozens = 12 + 12 we get 24,
4. 32 ÷ 2, 32 divided by 2 we get 12,
5. 24 – 4, subtracting 4 from 24 we get 20 and
6. 8 + 8, adding 8 to 8 we get 16,
Now 2 names that are not names for the number are
3. 2 dozen and 5. 24 -4, therefore the name of the box
on the tag is 16.