Everyday Mathematics 3rd Grade Answer Key Unit 7 Fractions
Everyday Mathematics Grade 3 Home Link 7.1 Answers
Liquid Volume Hunt
Family Note Today your child used a set of benchmark beakers to estimate and measure liquid volume in liters (L) and milliliters (mL). Liquid volume is a measure of how much liquid a container can hold. Help your child look at labels to find containers of liquids that are measured in milliliters and liters. Have your child record the items in the table below.
Please send clean, empty, unbreakable containers to school for our next lesson.
Question 1.
Examine labels on items for liquid volume measured in liters or milliliters. Record your findings in the table below.
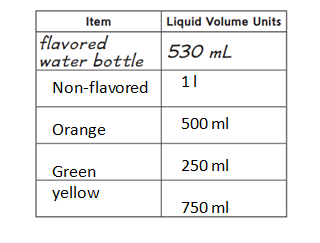
Answer:
Flavored water bottle = 530ml.
non-flavored water bottle = 1 liter.
orange color bottle = 500 ml.
green color bottle = 250 ml.
yellow color bottle = 750 ml.
Explanation:
In the above-given question,
given that,
Liquid volume is a measure of how much liquid a container can hold.
containers of liquids that are measured in milliliters and liters.
I am assuming the bottles with liquids.
Flavored water bottle = 530ml.
non-flavored water bottle = 1 liter.
orange color bottle = 500 ml.
green color bottle = 250 ml.
yellow color bottle = 750 ml.
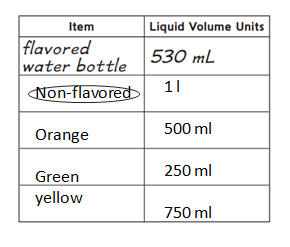
Question 2.
Circle an item that you can use as a benchmark for 1 liter.
Answer:
The item is non-flavored water bottle.
Explanation:
In the above-given question,
given that,
Liquid volume is a measure of how much liquid a container can hold.
containers of liquids that are measured in milliliters and liters.
I am assuming the bottles with liquids.
The item is non-flavored water bottle.
Question 3.
Put a star next to an item that you can use as a benchmark for 500 milliliters.
Answer:
The item is orange color bottle.
Explanation:
In the above-given question,
given that,
Liquid volume is a measure of how much liquid a container can hold.
containers of liquids that are measured in milliliters and liters.
I am assuming the bottles with liquids.
so the 500 ml contains orange color bottle.
Try This
Question 4.
Estimate the liquid volume of a clean dinner plate: about _________ mL
If you have a measuring tool marked with milliliters, find the liquid volume of your dinner plate by measuring how much water it holds before spilling over the edges.
about _________ mL
On the back of this page, explain how you found the liquid volume of the dinner plate.
Answer:
The dinner plate holds 500 ml of water before it spilling over the edges.
Explanation:
In the above-given question,
given that,
The clean dinner plate is about 500 ml.
Everyday Math Grade 3 Home Link 7.2 Answer Key
Exploring Equivalent Fractions
Family Note Today your child explored different representations of equal shares and played Fraction Memory. Help your child make sense of the Fraction Memory round below.
Question 1.
Nash chose these two cards in a round of Fraction Memory:
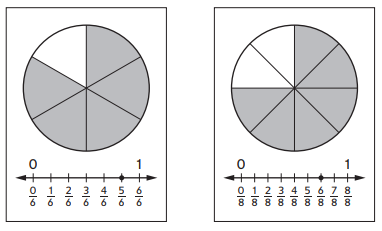
Nash says that these cards show equivalent fractions. Do you agree or disagree? Explain.
Answer:
No.
Explanation:
In the above-given question,
given that,
in 1st circle is shaded with 5/6 portion.
2nd circle is shaded with 6/8.
so both of the circles are not equal.
so disagree.
Practice
Solve.
Question 2.
6 × 9 = _________
Answer:
6 x 9 = 54.
Explanation:
In the above-given question,
given that,
Multiply.
6 x 9 = 54.
Question 3.
9 × 8 = _________
Answer:
9 x 8 = 72.
Explanation:
In the above-given question,
given that,
Multiply.
8 x 9 = 72.
9 x 8 = 72.
Question 4.
_________ = 7 × 8
Answer:
7 x 8 = 56.
Explanation:
In the above-given question,
given that,
Multiply.
7 x 8 = 56.
Everyday Mathematics Grade 3 Home Link 7.3 Answers
Number Stories with Measures
Family Note Today your child solved number stories involving time, volume, mass, and length. Help your child make sense of the stories below. Problems 1 and 2 are similar to those we solved in class. For the Try This problem, you may wish to remind your child that 2 halves make 1 whole.
Solve. Use drawings or number models to show your work.
Question 1.
The liquid volume of 1 juice box is about 150 mL. What is the liquid volume of 3 juice boxes?
about ![]()
Answer:
The liquid volume of 3 juice boxes = 450 ml.
Explanation:
In the above-given question,
given that,
The liquid volume of 1 juice box is about 150 ml.
150 + 150 = 300.
300 + 150 = 450.
150 x 3 = 450.
so the liquid volume of 3 juice boxes = 450 ml.
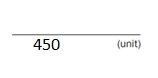
Question 2.
Art club ends at 3:30 P.M. Your mom arrives to pick you up at 3:10 P.M. If the teacher lets you out 5 minutes late, about how long does your mom have to wait?
about ![]()
Answer:
The number of minutes mom have to wait = 25 minutes.
Explanation:
In the above-given question,
given that,
Art club ends at 3:30 P.M.
Mom arrives to pick up at 3:10 P.M.
If the teacher lets you out 5 minutes late.
3:30 + 5 = 3:35.
3:35 – 3:10 = 3:25.
so the mom have to wait for 25 minutes.
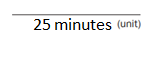
Try This
Question 3.
Anastasia’s water bottle has a liquid volume of about 1 liter. She drinks about 1 \(\frac{1}{2}\) bottles of water every day.
About how many liters of water does Anastasia drink in 5 days? You may draw a picture.
about ![]()
Answer:
The number of liters of water does Anastasia drink in 5 days = 7.5 liters.
Explanation:
In the above-given question,
given that,
Anastasia’s water bottle has a liquid volume of about 1 liter.
She drinks about 1 \(\frac{1}{2}\) bottles of water every day.
1 day = 1.5.
5 x 1.5 = 7.5.
so the number of liters of water does Anastasia drink in 5 days = 7.5 liters.

Everyday Math Grade 3 Home Link 7.4 Answer Key
Fraction Strips
Family Note Today your child made a set of fraction strips. Fraction strips are equal-length strips folded into equal parts. Each equal part is labeled with the appropriate unit fraction, such as \(\frac{1}{2}\) and \(\frac{1}{4}\). The strips can be used to compare fractions.
Help your child shade rectangles to show each fraction and write fractions that match the shaded parts.
Shade each rectangle to match the fraction below it.
Example: 
Question 1.
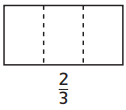
Answer:
2 boxes are filled out of 3 boxes.
Explanation:
In the above-given question,
given that,
there are 3 boxes.
out of 3 boxes,2 are filled.
2/3.
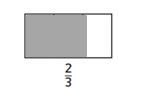
Question 2.
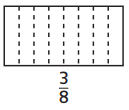
Answer:
3 boxes are filled out of 8 boxes.
Explanation:
In the above-given question,
given that,
there are 8 boxes.
out of 8 boxes,3 are filled.
3/8.
Question 3.
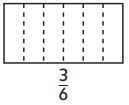
Answer:
3 boxes are filled out of 6 boxes.
Explanation:
In the above-given question,
given that,
there are 6 boxes.
out of 6 boxes,3 are filled.
3/6.

Question 4.
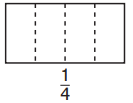
Answer:
1 box is filled out of 4 boxes.
Explanation:
In the above-given question,
given that,
there are 4 boxes.
out of 4 boxes,1 are filled.
1/4.
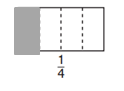
Compare the shaded parts of the fraction strips. Write >, <, or = to make the number sentence true

Question 5.
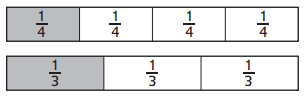
\(\frac{1}{4}\) ________ \(\frac{1}{3}\)
Answer:
1/4 < 1/3.
Explanation:
In the above-given question,
given that,
the numbers are 1/4 and 1/3.
1/4 = 0.25.
1/3 = 0.3.
0.25 < 0.3.
1/4 < 1/3.
Question 6.
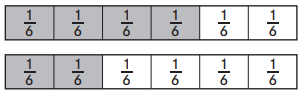
\(\frac{4}{6}\) __________ \(\frac{2}{6}\)
Answer:
4/6 > 2/6.
Explanation:
In the above-given question,
given that,
the numbers are 4/6 and 2/6.
4/6 = 0.6.
2/6 = 0.3.
0.6 > 0.3.
4/6 > 2/6.
Practice
Make an estimate. Then show how you solve each problem on the back of this page. Explain to someone how you can use your estimate to check whether your answer makes sense.
Question 7.
963 – 548 = __________
My estimate: __________
Answer:
963 – 548 = 415.
Explanation:
In the above-given question,
given that,
difference.
963 – 548 = 415.
950 – 550 = 400.
Question 8.
412 + 298 = __________
My estimate: __________
Answer:
412 + 298 = 710.
Explanation:
In the above-given question,
given that,
Addition.
412 + 298 = 710.
400 + 300 = 700.
Everyday Mathematics Grade 3 Home Link 7.5 Answers
Fractions on Number Lines
Family Note Today your child learned about fractions as numbers on a number line. Children made their own Fraction Number-Line Posters by dividing number lines from 0 to 1 into equal-size parts, or distances. They labeled the tick marks with the appropriate fractions. Support your child in locating fractions on the number lines below.
Question 1.
Write the fraction that represents the distance the triangle moved.

Answer:
The missing fractions are 1/2 and 3/8.
Explanation:
In the above-given question,
given that,
some of the fractions are missing.
the missing fractions are 1/2 and 3/8.
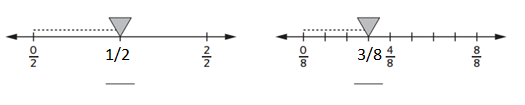
Question 2.
Write the missing fractions.

Answer:
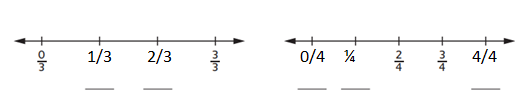
The missing fractions are 1/3, 2/3, 0/4, 1/4, and 4/4.
Explanation:
In the above-given question,
given that,
the number lines.
some of the fractions are missing.
the missing fractions are 1/3.
1/3 + 1/3 = 2/3.
1/3 and 2/3.
0/4 + 1 = 1/4.
1/4 + 3 = 4/4.
Practice
Fill in the unit. Solve. Show your work.
Question 3.
333 + 492 = _________
Answer:
333 + 492 = 825.
Explanation:
In the above-given question,
given that,
Addition.
333 + 492 = 825.
Question 4.
_______ = 888 – 678
Answer:
888 – 678 = 210.
Explanation:
In the above-given question,
given that,
Subtraction.
888 – 678 = 210.
Everyday Math Grade 3 Home Link 7.6 Answer Key
More Fractions on Number Lines
Family Note Today your child identified fractions that are less than or greater than 1 on number lines. Help your child count the number of equal parts or distances between 0 and 1 and label each tick mark with a fraction.
For each number line, fill in the missing numbers. Then name the fraction at each point.
Question 1.

_________ names the point on the number line.
Answer:
The missing fractions are 1/3, 2/3.
Explanation:
In the above-given question,
given that,
the numbers on the number line.
0/3 + 1 = 1/3.
1/3 + 1 = 2/3.
so the missing numbers are 1/3, 2/3.
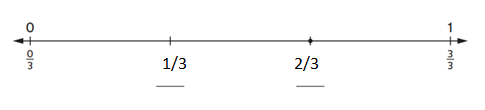
Question 2.
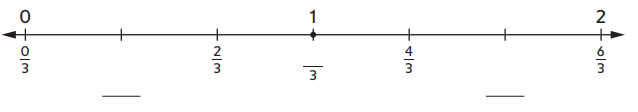
_________ names the point on the number line.
Answer:
The missing fractions are 1/3, 3/3, 5/3.
Explanation:
In the above-given question,
given that,
the numbers on the number line.
1/3 + 1 = 2/3.
2/3 + 1 = 3/3.
4/3 + 1 = 5/3.
so the missing numbers are 1/3, 3/3, 5/3.
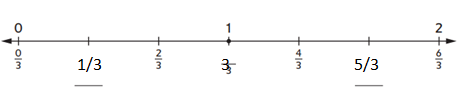
Question 3.
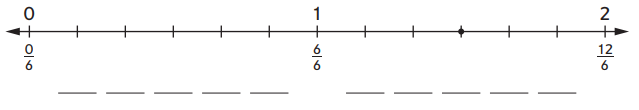
_________ names the point on the number line.
Answer:
The missing fractions are 1/6, 2/6, 3/6, 4/6, 5/6, 7/6, 8/6, 9/6, 10/6, 11/6.
Explanation:
In the above-given question,
given that,
the numbers on the number line.
0/6 + 1 = 1/6.
1/6 + 1 = 2/6.
2/6 + 1 = 3/6.
3/6 + 1 = 4/6.
4/6 + 1 = 5/6.
6/6 + 1 = 7/6.
7/6 + 1 = 8/6.
8/6 + 1 = 9/6.
9/6 + 1 = 10/6.
10/6 + 1 = 11/6.
so the missing numbers are 1/6, 2/6,3/6, 4/6, 5/6, 7/6, 8/6, 9/6, 10/6, 11/6.
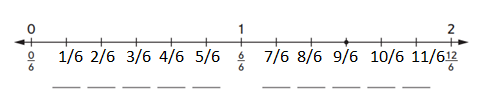
Question 4.
Look at the point on each number line. Which point names a fraction greater than 1?
Answer:
The fraction greater than 1 is 9/6.
Explanation:
In the above-given question,
given that,
the fraction greater than 1.
6/6 = 1.
Practice
Fill in the unit. Solve. Show your workon the back of this page.
Question 5.
549 – 289 = ________
Answer:
549 – 289 = 260.
Explanation:
In the above-given question,
given that,
Subtraction.
549 – 289 = 260.
Question 6.
739 + 261 = _________
Answer:
739 + 261 = 1000.
Explanation:
In the above-given question,
given that,
Addition.
739 + 261 = 1000.
Everyday Mathematics Grade 3 Home Link 7.7 Answers
Comparing Fractions to \(\frac{1}{2}\)
Family Note Today your child wrote number sentences comparing fractions shown with fraction circles and number lines. Ask your child to explain whether the fractions represented below are greater than (>), less than (<), or equal to (=) \(\frac{1}{2}\)
Shade each circle to match the fraction below it.
Example:
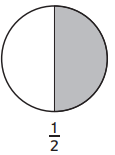
Question 1.
Answer:
2 boxes are filled out of 3 boxes.
Explanation:
In the above-given question,
given that,
the circle is divided into 3 parts.
out of 3 parts 2 parts are filled.
2/3.
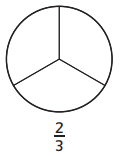
Question 2.
Answer:
3 boxes are filled out of 6 boxes.
Explanation:
In the above-given question,
given that,
the circle is divided into 6 parts.
out of 6 parts 3 parts are filled.
3/6.
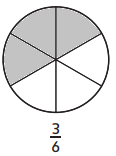
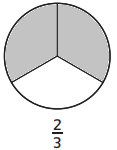
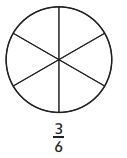
Question 3.
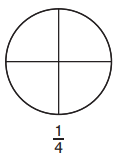
Answer:
1 box are filled out of 4 boxes.
Explanation:
In the above-given question,
given that,
the circle is divided into 4 parts.
out of 4 parts 1 part are filled.
1/4.
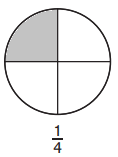
Look at the shaded parts of the circles.
Question 4.
Write the fraction above that is less than \(\frac{1}{2}\).
Answer:
1/4.
2 boxes are filled out of 3 boxes.
Explanation:
In the above-given question,
given that,
1/2 = 0.5.
1/4 = 0.25.
1/4 < 1/2.
Question 5.
Write the fraction above that is equal to \(\frac{1}{2}\).
Answer:
3/6.
Explanation:
In the above-given question,
given that,
3/6 = 0.5.
1/2 = 0.5.
Question 6.
Write the fraction above that is greater than \(\frac{1}{2}\).
Answer:
2/3.
Explanation:
In the above-given question,
given that,
2/3 = 0.6.
1/2 = 0.5.
Question 7.
Write <, >, or = to make the sentence true. You may draw a picture to help.
\(\frac{3}{4}\) __________ \(\frac{1}{4}\)
Answer:
3/4 > 1/4.
Explanation:
In the above-given question,
given that,
the numbers are 3/4 and 1/4.
3/4 = 0.75.
1/4 = 0.25.
0.75 > 0.25.
Everyday Math Grade 3 Home Link 7.8 Answer Key
Sorting Fractions
Family Note Today your child looked for patterns to help order fractions with the same numerator. Children recognized that as a fraction’s denominator gets larger the fraction gets smaller. They were able to write this as a rule for ordering fractions with the same numerator. For Problem 1, your child will sort a set of fractions into two groups: fractions greater than 1 and fractions less than 1. In Problem 2, your child will look for patterns to help sort any set of fractions into these two groups.
Question 1.
Look at the fractions below and sort them into two groups: fractions less than 1 and fractions greater than 1. Use the number lines on the following page to help you.
\(\frac{1}{2}, \frac{2}{3}, \frac{6}{4}, \frac{3}{2}, \frac{7}{8}, \frac{5}{3}, \frac{6}{8}, \frac{7}{6}\)

Answer:
The fraction less than 1 = 1/2, 2/3, 7/8, 6/8.
The fraction greater than 1 = 6/4, 3/2, 5/3, 7/6.
Explanation:
In the above-given question,
given that,
the fractions are 1/2, 2/3, 7/8, 6/8, 6/4, 3/2, 5/3, 7/6.
the fractions less than 1 = 1/2, 2/3, 7/8, 6/8.
the fraction greater than 1 = 6/4, 3/2, 5/3, 7/6.

Question 2.
Look for a pattern in the fractions you sorted. Describe a pattern that can help you decide whether a fraction is less than 1 or greater than 1.
Fraction Number Lines
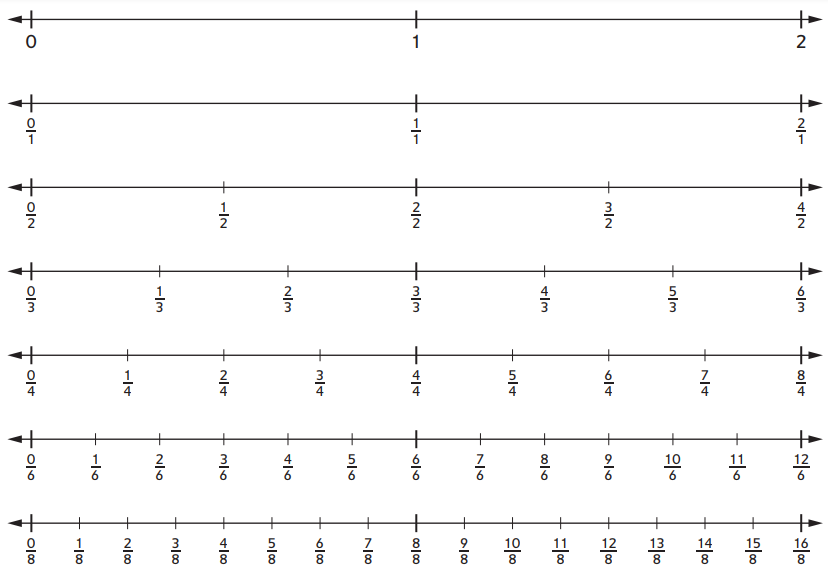
Answer:
The fractions that are less than 1 is the numerator is less than the denominator.
the fractions that are greater than 1 is the numerator is greater than the denominator.
Explanation:
In the above-given question,
given that,
the fractions less than 1 are 1/2, 1/3, 1/4, 2/3, 3/4.
the fraction greater than 1 are 16/8, 15/8, 14/8, 13/8, 12/8 ….
Everyday Mathematics Grade 3 Home Link 7.9 Answers
Locating Fractions on Number Lines
Family Note Today your child learned to partition, or divide, number lines into equal parts and then locate and label fractions between whole numbers. The denominator of the given fraction describes the number and size of the equal parts. A whole on each number line below is equal to the distance between 0 and 1.
Partition the wholes on each number line. Then locate and label the given fractions. Tell someone at home how you partitioned your number lines.
Question 1.
\(\frac{1}{2}\)

Answer:
The missing fractions are 1/2.
Explanation:
In the above-given question,
given that,
the fraction is 1/2.
1/2 is located in the middle of the number line.
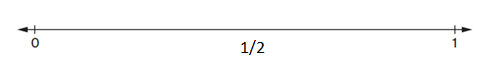
Question 2.
\(\frac{1}{4}\)

Answer:
The missing fractions are 1/4.
Explanation:
In the above-given question,
given that,
the fraction is 1/4.
1/4 is located in the middle of the number line.

Question 3.
\(\frac{2}{3}\)

Answer:
The missing fractions are 2/3.
Explanation:
In the above-given question,
given that,
the fraction is 2/3.
2/3 is located in the right side of the number line.
Question 4.
\(\frac{5}{6}\)

Answer:
The missing fractions are 5/6.
Explanation:
In the above-given question,
given that,
the fraction is 5/6.
5/6 is located in the right side of the number line.

Try This
Question 5.
\(\frac{3}{2}\)

Answer:
The missing fractions are 3/2.
Explanation:
In the above-given question,
given that,
the fraction is 3/2.
3/2 is located in the right side of the number line.

Everyday Math Grade 3 Home Link 7.10 Answer Key
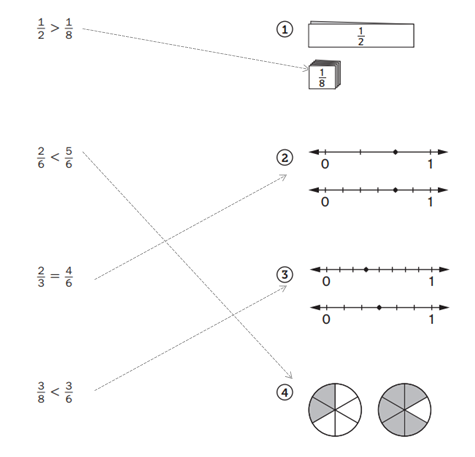
Matching Fraction Tools
Family Note Your child has been using number lines, fraction circles, and fraction strips to learn about and represent fractions. Today your child used these tools to make and justify fraction comparisons. Encourage your child to explain how he or she matched each number sentence with a picture that represents the fraction comparison.
Draw a line from each number sentence to the picture that represents it.
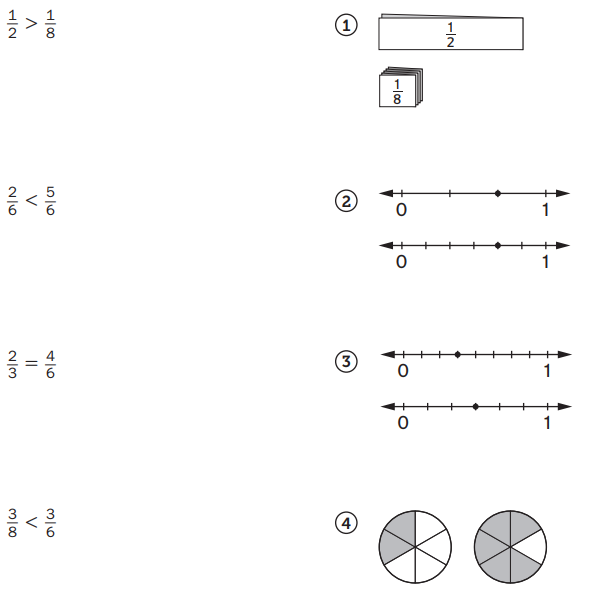
On the back of this page, write one of the above fraction number sentences. Sketch a different fraction tool that shows the same comparison.
Answer:
1/2 > 1/8.
Explanation:
In the above-given question,
given that,
2/6 < 5/6 is matched with circles.
Everyday Mathematics Grade 3 Home Link 7.11 Answers
Fraction Number Stories
Family Note Today your child solved fraction number stories using a variety of fraction models, including pictures. Encourage your child to sketch a picture to represent each story.
Solve these number stories. Show your answer as a fraction. You may draw pictures to show your work.
Question 1.
Ralph read \(\frac{1}{8}\) of his book. What fraction of the book does he still have left to read?
My sketch:
____________ of his book
Answer:
The fraction of the book does he still has left to read = 7/8.
Explanation:
In the above-given question,
given that,
Ralph read 1/8 of his book.
1/8 + 7/8 = 8/8.
8/8 = 1.
so the fraction of the book does he still have left to read = 7/8.
Question 2.
Four friends equally share two bottles of juice. How much juice will each friend get?
My sketch:
____________ of a bottle of juice
Answer:
The fraction of juice will each friend gets = 1/2.
Explanation:
In the above-given question,
given that,
Four friends equally share two bottles of juice.
1/4 + 1/4 = 2/4.
2/4 = 1/2.
so the fraction of juice will each friend gets = 1/2.
Question 3.
Nora rode her bike \(\frac{2}{2}\) of a block. Brady rode his bike \(\frac{4}{4}\) of the same block. Compare the distances each child rode. What do you notice?
Explain your answer.
My sketch:
Answer:
They both rode the same distance.
Explanation:
In the above-given question,
given that,
Nora rode her bike 2/2 = 1 of a block.
Brady rode his bike 4/4 = 1 of the same block.
so they both rode the same distance.
Everyday Math Grade 3 Home Link 7.12 Answer Key
Fractions of Collections
Family Note Today your child used fractions to name parts of collections of objects. As you help your child, encourage him or her to use sketches, pennies, or other tools to solve the number stories.
Solve. Explain to someone at home how you figured out the numerator and the denominator for each fraction in Problems 1–3.
Question 1.
12 dogs are in the park. 2 of them are chasing a ball.
What fraction of the dogs are chasing a ball? ________
Answer:
The fraction of the dogs are chasing a ball = 2/12.
Explanation:
In the above-given question,
given that,
12 dogs are in the park.
2 of them are chasing a ball.
2/12 = 1/6.
so the fraction of the dogs are chasing a ball = 2/12.
Question 2.
7 children are waiting for the school bus. 4 of them are girls.
What fraction of the children are girls? ________
Answer:
The fraction of the children are girls = 4/7.
Explanation:
In the above-given question,
given that,
7 children are waiting for the school bus.
4 of them are girls.
4/7.
so the fraction of the children are girls = 4/7.
Question 3.
There are 16 tulips in the garden. 4 of them are red.
What fraction of the tulips are not red? ________
Answer:
The fraction of the tulips are not red = 12/16.
Explanation:
In the above-given question,
given that,
There are 16 tulips in the garden.
4 of them are red.
16 – 4 = 12.
12/16.
Question 4.
Lisa and Carlie each have 6 cups. \(\frac{2}{6}\) of Lisa’s cups are yellow. \(\frac{4}{6}\) of Carlie’s cups are yellow. Who has more yellow cups?
Draw a picture to show your thinking.
________ has more yellow cups.
Answer:
Carlie has more yellow cups.
Explanation:
In the above-given question,
given that,
Lisa and Carlie each have 6 cups.
2/6 of Lisa’s cups are yellow.
4/6 of Carlie’s cups are yellow.
2/6 = 0.33.
4/6 = 0.6.
so Carlie has more yellow cups.
Practice
Fill in the un it. Solve. Show your work on the back of this page.
Question 5.
476 = 741 – ________
Answer:
741 – 265 = 476.
Explanation:
In the above-given question,
given that,
Subtraction.
265 + 476 = 741.
741 – 265 = 476.
Question 6.
558 = ________ – 328
Answer:
886 – 328 = 558.
Explanation:
In the above-given question,
given that,
subtraction.
558 + 328 = 886.
886 – 328 = 558.