Everyday Math Grade 3 Answers Unit 4 Measurement and Geometry

Everyday Mathematics 3rd Grade Answer Key Unit 4 Measurement and Geometry

Everyday Mathematics Grade 3 Home Link 4.1 Answers

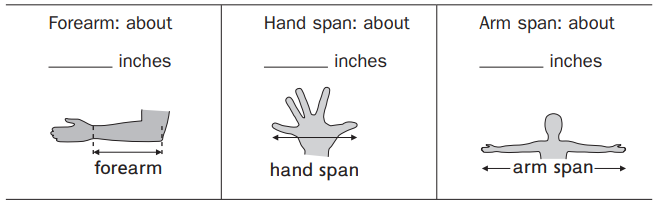
Body Measures

Family Note Today your child measured to the nearest half inch. Help your child measure an adult at home. Use a tape measure if available, or mark lengths on a piece of string and then measure the string with a ruler.

Measure an adult at home to the nearest \(\frac{1}{2}\) inch. Fill in the information below:
Name of adult: ___________
Height: about ___________ inches
Length of shoe: about ___________ inches
Around neck: about ___________ inches
Around wrist: about ___________ inches
Distance from waist to floor:
about ___________ inches

Practice
Fill in the unit box. Solve. Show your work in the space below.

Question 1.
_______ = 293 + 145
Answer:

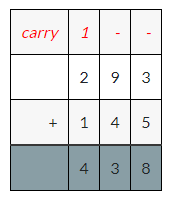
Explanation:
The sum of 293 and 145 is 438.

Question 2.
326 – 158 = ________
Answer:

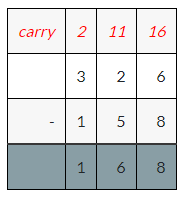
Explanation:
The difference between 326 and 158 is 168.

Everyday Math Grade 3 Home Link 4.2 Answer Key

Describing Data

Family Note Today your child represented shoe-length measures on a line plot. Help your child answer questions about the line plot below.

Children in the Science Club collected pill bugs. The tally chart shows how many they collected. Use the data from the tally chart to complete the line plot.

Use the information in the line plot to answer the questions.
Question 1.
What is the greatest (maximum) number of pill bugs found? ________
Answer:
6

Explanation:
The number of pills are given on the left side of the above table, the greatest(maximum) number of pillbugs found by children in science lab are 6.

Question 2.
What is the least (minimum) number of pill bugs found? _________
Answer:
2

Explanation:
The number of pills are given on the left side of the above table, the least(minimum) number of pillbugs found by children in science lab are 2.

Question 3.
How many pill bugs were collected all together? _________
Answer:

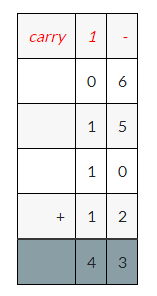
Explanation:
3 students collected 2 pill bugs, 3 x 2 = 6
5 students collected 3 pill bugs, 5 x 3 = 15
2 students collected 5 pill bugs, 2 x 5 = 10 and
2 students collected 6 pill bugs 2 x 6 = 12.
Add 6, 15, 10 and 12.
Therefore 6+15+10+12=43

Practice
Think how the first fact can help you solve the second. Draw an array to show your strategy. Then solve.
Question 4.
2 × 7 = _________
3 × 7 = _________
Answer:

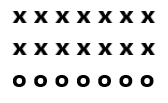
Explanation:
There are 7 cross marks in 2 rows, first fact is 7+7=14, and there are 7 o’s in the third row so, second fact is 7+7+7=21.

Question 5.
5 × 6 = _________
4 × 6 = _________
Answer:
5 x 6 = 30
4 x 6 = 24

Explanation:
There are 6 cross marks in 5 rows, first fact is 6+6+6+6+6=30, and if we remove a row,we are left with 6 cross marks in 4 rows

Everyday Mathematics Grade 3 Home Link 4.3 Answers

Measuring Distances Around Objects

Family Note Today your child measured the distance around his or her head and wrist, as well as around different objects in the classroom. Finding the distance around objects helps children understand perimeter, which is formally introduced in Lesson 4-6. It is also good practice for measuring to the nearest \(\frac{1}{2}\) inch.

Talk to someone at home about finding the distances around objects.
Question 1.
What tools can be used to measure the distance around an object?
Answer: Tape measure, toolkit ruler, 12 inch ruler, string and yardstick

Question 2.
Choose two objects in your home, such as a small picture frame and a book. Choose a measuring tool and use it to measure the distance around each object to the nearest \(\frac{1}{2}\) inch.
Object: _________ Measurement: about _________ inches
Object: _________ Measurement: about _________ inches
What measuring tool did you use? ________________
Answer:
Object: Book Measurement: about 11 inches
Object: Photo frame Measurement: about 6 inches
What measuring tool did you use? Ruler

Practice
Think of how the first fact can help you solve the second. Then solve both. You may draw arrays to help.
Question 3.
5 × 7 = _________
6 × 7 = _________
Answer:
The product of two numbers 5 and 7 is
5 × 7 = 35
The product of two numbers 6 and 7 is
6 × 7 = 42

Question 4.
10 × 6 = _________
9 × 6 = _________
Answer:
The product of two numbers 10 and 6 is
10 × 6 = 60
The product of two numbers 9 and 6 is
9 × 6 = 54

Question 5.
5 × 8 = _________
6 × 8 = _________
Answer:
The product of two numbers 5 and 8 is
5 × 8 = 40
The product of two numbers 6 and 8 is
6 × 8 = 48

Question 6.
10 × 7 = _________
9 × 7 = _________
Answer:
The product of two numbers 10 and 7 is
10 × 7 = 70
The product of two numbers 9 and 7 is
9 × 7 = 63

Everyday Math Grade 3 Home Link 4.4 Answer Key

Polygons

Family Note Today your child learned the names of different polygons. A polygon is a 2-dimensional shape with only straight sides that meet end to end to make one closed path. The sides may not cross one another. Polygons are named by the number of sides they have. Polygons are all around us. For example, a stop sign is an octagon, an 8-sided polygon, and this Home Link page is a rectangle, a 4-sided polygon with 4 right angles (square corners).

Question 1.
Cross out the shapes that are not polygons.

How do you know which shapes are not polygons?
Answer:
The third and fifth shapes should be crossed out,
Polygons have straight sides that do not cross.
The shapes I crossed out have curved sides or sides that cross

Question 2.
Cut out pictures of shapes from newspapers and magazines to match each of the descriptions below. Tape or glue your pictures on the front or back of this page .

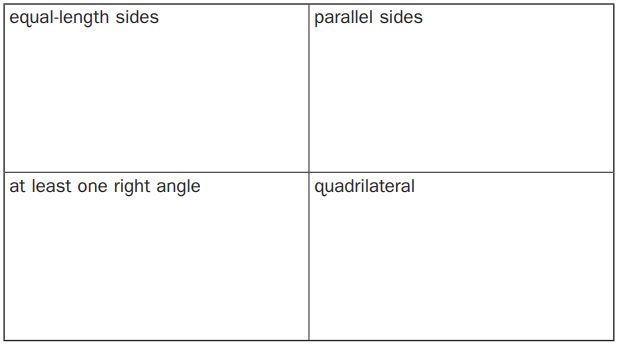
Answer:

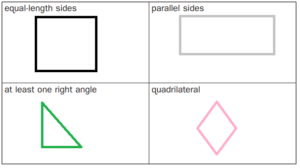
Everyday Mathematics Grade 3 Home Link 4.5 Answers

Special Quadrilaterals

Family Note Today your child learned about six different categories of quadrilaterals, which are polygons that have four sides: squares, rectangles, rhombuses, parallelograms, trapezoids, and kites. Although these categories have specific definitions, a particular shape may fall into more than one category.

Question 1.
Name the two special quadrilaterals below.

How are these two shapes alike? _____________
How are they different? _____________
Answer:
Square, Rhombus, Both shapes have 4 same length sides.
A square has to have 4 right angles.
A rhombus does not have to have all 4 right angles.

Question 2.
Name the two special quadrilaterals below.

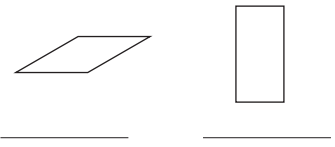
How are these two shapes alike? _____________
How are they different? _____________
Answer:
Rhombus, rectangle both shapes have 2 pairs of equal opposite sides.
A rhombus has all 4 equal-length sides.
A rectangle has 4 right angles.

Everyday Math Grade 3 Home Link 4.6 Answer Key

Perimeter

Family Note Today your child found the perimeters of several polygons. Perimeter is the distance around a 2-dimensional shape. Finding perimeters gives your child practice measuring to the nearest \(\frac{1}{2}\) inch and the nearest whole centimeter.

If you do not have a ruler at home, cut out and use the 6-inch ruler on the next page. Measure the sides of each polygon to the nearest \(\frac{1}{2}\) inch. Use the side lengths to find the perimeter of each polygon. Write a number sentence to show how you found the perimeter.
Question 1.

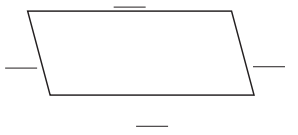
Number sentence: _____________
Perimeter: about _____________ inches
Answer:
Let the base = 2 inches
Height = 1 in
2 + 2 + 1 + 1 = 6
Perimeter is about 6 inches

Question 2.

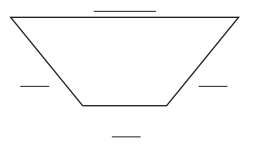
Number sentence: _____________
Perimeter: about _____________ inches
Answer:
l1 = 2 \(\frac{1}{2}\) in
l2 = 1 in
w = 1 in
Perimeter: 2 \(\frac{1}{2}\) + 1 + 1 + 1 = 5 \(\frac{1}{2}\) inches

Find the perimeters of the square and the rectangle below.
Question 3.

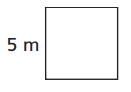
Number sentence: _____________
Perimeter: _____________ meters (m)
Answer:
The above figure is a square. All the sides of a square is equal.
Perimeter of a square = 4s
P = 4 × 5 m = 20 meter

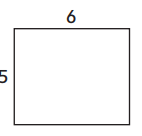
Question 4.

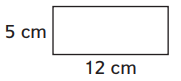
Number sentence: _____________
Perimeter: _____________ centimeters (cm)
Answer:
L = 12 cm
W = 5 cm
Area = L.W
= 12 × 5 = 60 sq. cm
Perimeter = 12 + 12 + 5 + 5 = 34 centimeters

Question 5.
Draw a quadrilateral below. Find the perimeter to the nearest \(\frac{1}{2}\) inch.
Answer:

Everyday Mathematics Grade 3 Home Link 4.7 Answers

Perimeter and Area

Family Note Today your child compared measuring perimeter to measuring area using 1-foot squares. Perimeter is the distance around a shape. It can be measured in units of length, such as centimeters, inches, feet, and so on. Area is the measure of surface space inside the boundary of a shape. It can be measured in square units, such as square centimeters, square inches, square feet, and so on. To measure perimeter, children used the edges of 1-foot squares as their units. To measure area, they used the area of 1-foot squares as their units.

Trace the boundary of the rectangle with a crayon to show where you measure the perimeter.
With a different colored crayon, shade the surface inside the rectangle to show where you measure area.
Question 1.

Dale said the perimeter of this rectangle is 16 feet and the area is 12 square feet. Do you agree? Explain.
Answer:
I agree. The perimeter is the total length of sides,
2 + 2 + 6 + 6 = 16.
The area is the number of squares inside the rectangle.

Your pace is the length of one of your steps.

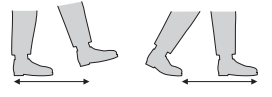
Question 2.
Find the perimeter, in paces, of your bedroom. Walk along each side and count the number of paces.
The perimeter of my bedroom is about _____________ paces.
Answer: The perimeter of my bedroom is about 7 paces.

Question 3.
Which room in your home has the largest perimeter? Use your estimating skills to help you decide.
The _____________ has the largest perimeter.
Its perimeter is about _____________ paces.
Answer: The living room has the largest perimeter.
Its perimeter is about 25 paces.

Everyday Math Grade 3 Home Link 4.8 Answer Key

Areas of Rectangles

Family Note Today your child found areas of rectangles using composite units. Composite units are made up of two or more square units. Using composite units to find area helps children see a rectangle as having a row-by-column structure, and it helps them measure area more efficiently.

Question 1.
Sarah tiled her floor with square tiles. This is a drawing of her floor:
Shade a composite unit made of 10 squares. Use the composite unit to figure out the number of tiles Sarah needs.
Sarah needs _____________ tiles.

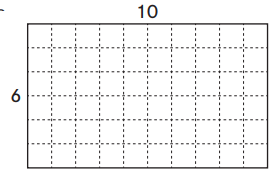
Answer:
Given,
Shade a composite unit made of 10 squares.
6 × 10 = 60 tiles
Thus Sarah needs 60 tiles.

Question 2.
Alejandro painted a wall that is 3 yards tall and 7 yards long. This is a drawing of the wall:

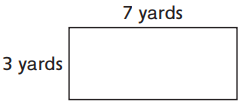
Partition the rectangle to show 3 rows with 7 squares in each row. Shade a composite unit made of 3 squares. Then figure out the area of the wall.
How many square yards did Alejandro paint? _____________ square yards
Answer:
Partition the rectangle to show 3 rows with 7 squares in each row
3 × 7 = 21 square yards

Question 3.
Explain how you found the area of the wall in Problem 2.
Answer:
I made a composite unit of a column of 3 squares and counted by 3s seven times to get 21.

Everyday Mathematics Grade 3 Home Link 4.9 Answers

Arrays, Side Lengths, and Area

Family Note Today your child learned that side lengths of rectangles correspond to the number of square units in the rectangles’ rows and columns. Just as rows and columns in arrays can be multiplied to find total numbers of objects, side lengths can be multiplied to find areas of rectangles.

Make a dot inside each small square in one row. Then fill in the blanks.
Question 1.
Number of rows: _____________
Number of squares in a row: _____________
Number sentence: _____________ × _____________ = _____________
Area: _____________ square units

Answer:
Number of rows: 7
Number of squares in a row: 5
Number sentence: Seven × Five = Thirty Five
7 × 5 = 35 sq. units
Area: 35 square units

Question 2.
Number of rows: _____________
Number of squares in a row: _____________
Number sentence: _____________ × _____________ = _____________
Area: _____________ square units

Answer:
Number of rows: 6
Number of squares in a row: 7
Number sentence: 6 × 7 = 42
Area: 42 square units

Mark the dots to show each array. Then fill in the blanks.
Question 3.

Make a 4-by-8 array.
Number sentence: _____________ × _____________ = _____________
Answer:
4 × 8 = 32

Question 4.

Make a 9-by-5 array.
Number sentence: _____________ × _____________ = _____________
Answer: 9 × 5 = 45

Everyday Math Grade 3 Home Link 4.10 Answer Key

Area and Perimeter

Family Note Today your child learned how to play The Area and Perimeter Game to practice finding the areas and the perimeters of rectangles.

Find the area and the perimeter of each rectangle.
Question 1.

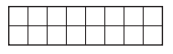
This is a 2-by-8 rectangle.
Area: _______ square units
Perimeter: ________ units
Answer:
Area:
2 × 8 = 16 square units
Perimeter = 2 + 2 + 8 + 8 = 20 units

Question 2.

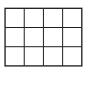
This is a 3-by-4 rectangle.
Area: _______ square units
Perimeter: ________ units
Answer:
Area:
3 × 4 = 12 sq. units
Perimeter:
3 + 3 + 4 + 4 = 14 units

Question 3.
What strategies did you use to solve Problem 2?
Answer:
I multiplied two side lengths to find the area:
3 × 4 = 12.
I added the side lengths to find the perimeter: 3 + 3 + 4 + 4 = 14 units

Try This
Question 4.

This is a 5-by-6 rectangle.
Area: ________ square units
Perimeter: ________ units
What strategies did you use?
Answer:
Area: 5 × 6 = 30 sq. units
Perimeter : 5 + 5 + 6 + 6 = 22 units
We can find the area by multiplying 5 with 6 we get 30.
Next we have to add the side lengths and double the total to find the perimeter:
5 + 6 = 11 and 11 × 2 = 22

Everyday Mathematics Grade 3 Home Link 4.11 Answers

Working with Perimeter and Area

Family Note Today your child solved problems involving perimeter, the distance around a shape, and area, the amount of surface inside a shape. Ask your child to explain how area and perimeter are used in solving the two problems below.

Question 1.
All of the sides of the two figures below are 2 feet long. Find the perimeter of each figure. Remember to write the units with your answers.

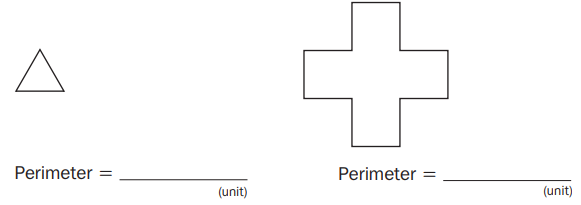
Answer: Perimeter: 2 + 2 + 2 = 6 units
Perimeter: 4 × 6 = 24 units

Question 2.
Sue wants to paint the longest wall in her bedroom pink. She measured the wall and found that it is 10 feet long and 8 feet tall. When she went to the hardware store to buy paint, Sue learned that 1 quart of paint can cover 50 square feet.
Sue should buy of paint.
Show how you figured out how much paint Sue will need.
Answer: 2 quarts

Everyday Math Grade 3 Home Link 4.12 Answer Key

Finding the Area of Rectilinear Figures

Family Note Today your child learned how to find the area of a rectilinear figure (a polygon whose sides all meet to make right angles) by decomposing, or separating, it into smaller rectangles. Help your child follow the steps to find the area of the rectilinear figure below.

Question 1.
Partition the shape into 2 or 3 rectangles.
Answer:

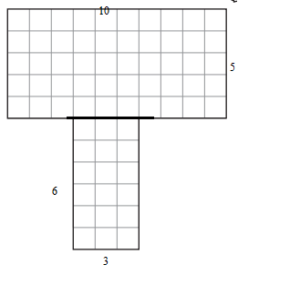
Question 2.
Find the area of each rectangle.
Answer:
Area of rectangle 1:
A = 5 × 10 = 50 sq. units
Area of rectangle 2:
A = 6 × 3 = 18 sq. units

Question 3.
Add the areas of the rectangles to find the area of the whole shape.
Answer:
area of the whole shape = 50 + 18 = 68 sq. units

Question 4.

Area of whole shape: ___________ square units
Answer:
Sample:
5 × 10 = 50
6 × 3 = 18
50 + 18 = 68
Thus the area is 68 sq. units

Question 5.
How can the area of each rectangle help you find the area of the whole shape?
Answer: I can find the area of each rectangle and then add the two together to get the area of the whole shape.