Engage NY Eureka Math Precalculus Module 4 Lesson 9 Answer Key
Eureka Math Precalculus Module 4 Lesson 9 Exercise Answer Key
Exercises
Exercise 1.
Find the value of x in the triangle below.
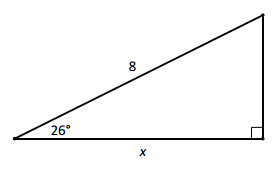
Answer:
We have cos(26°) = \(\frac{x}{8}\). This means x = 8∙cos(26°) ≈ 7.2.
Exercise 2.
Explain how the figures below are related. Then, describe x in terms of ϑ.
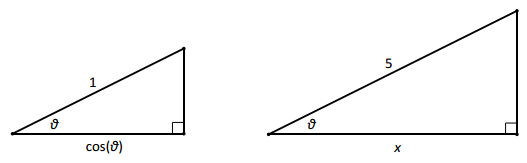
Answer:
The triangles above are similar. We can produce the triangle at the right by dilating the triangle at the left using a scale factor of 5. This means that x = 5∙cos(ϑ).
Exercise 3.
Find the length of side \(\overline{A C}\) in the triangle below.
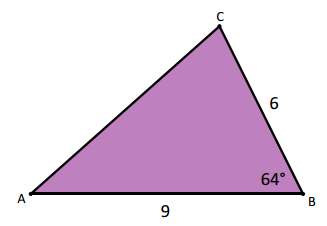
We have 6∙cos(64°) ≈ 2.6 and 6∙sin(64°) ≈ 5.4. Then we have 9 – 2.6 = 6.4. Finally, we have \(\sqrt{6.4^{2} + 5.4^{2}}\) ≈ 8.4.
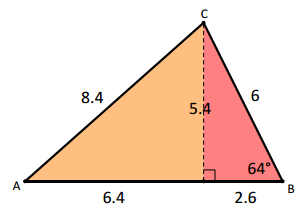
Exercise 4.
Points B and C are located at the edges of a large body of water. Point A is 6 km from point B and 10 km from point C. The angle formed between \(\overline{B A}\) and \(\overline{A C}\) is 108°. How far apart are points B and C?
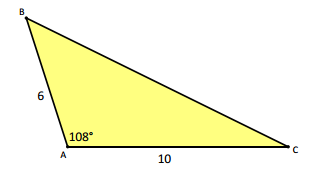
Answer:
62 + 102 = BC2 + 2(6)(10)∙cos(108°)
136 = BC2 + 120∙cos(108°)
BC2 = 136 – 120∙cos(108°)
BC ≈ 13.2
Exercise 5.
Use the law of cosines to find the value of ϑ in the triangle below.
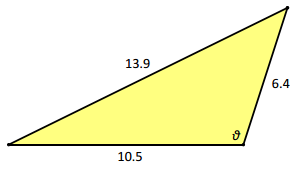
Answer:
10.52 + 6.42 = 13.92 + 2(10.5)(6.4)∙cos(ϑ)
– 42 = 134.4∙cos(ϑ)
m∠ϑ ≈ 108°
Eureka Math Precalculus Module 4 Lesson 9 Problem Set Answer Key
Question 1.
Consider the case of a triangle with sides 5, 12, and the angle between them 90°.
a. What is the easiest method to find the missing side?
Answer:
Pythagorean theorem
b. What is the easiest method to find the missing angles?
Answer:
Right triangle trigonometry
c. Can you use the law of cosines to find the missing side? If so, perform the calculations. If not, show why not.
Answer:
Yes, this is an example of SAS. The missing side is 13.
d. Can you use the law of cosines to find the missing angles? If so, perform the calculations. If not, show why not.
Answer:
Yes. The measures of the missing angles are 22.62° and 67.38°.
e. Consider a triangle with sides a, b, and the angle between them 90°. Use the law of cosines to prove a well – known theorem. State the theorem.
Answer:
c2 = a2 + b2 – 2ab cos(90°)
c2 = a2 + b2 – 2ab⋅0
c2 = a2 + b2
The Pythagorean theorem
f. Summarize what you have learned in parts (a) through (e).
Answer:
The law of cosines appears to be a more general form of the Pythagorean theorem, one that can work with any angle between two sides of a triangle, not just a right angle.
Question 2.
Consider the case of \(\overline{C A}\) and \(\overline{C B}\) of lengths 5 and 12, respectively, with m∠C = 180°.
a. Is ABC a triangle?
Answer:
\(\overline{A B}\) is a line segment containing C. △ABC does not exist.
b. What is the easiest method to find the distance between A and B?
Answer:
Add the lengths of the two line segments partitioning \(\overline{A B}\): 5 + 12 = 17.
c. Can you use the law of cosines to find the distance between A and B? If so, perform the calculations. If not, show why not.
Answer:
Yes. 52 + 122 – 2⋅5⋅12 cos(180°) = 25 + 144 + 120 = 289 = 172
The distance between A and B is 17 units.
d. Summarize what you have learned in parts (a) through (c).
Answer:
The law of cosines can work even when the line segments are a linear pair and do not form a triangle.
Question 3.
Consider the case of \(\overline{C A}\) and \(\overline{C B}\)of lengths 5 and 12, respectively, with m∠C = 0°.
a. Is ABC a triangle?
Answer:
\(\overline{C B}\) is a line segment containing A. △ABC does not exist.
b. What is the easiest method to find the distance between A and B?
Answer:
Subtract the two line segments: 12 – 5 = 7.
c. Can you use the law of cosines to find the distance between A and B? If so, perform the calculations. If not, show why not.
Answer:
Yes, the law of cosines still applies. 52 + 122 – 2⋅5⋅12 cos(0°) = 25 + 144 – 120 = 49 = 72
The distance between A and B is 7 units.
d. Summarize what you have learned in parts (a) through (c).
Answer:
The law of cosines applies even when the line segments have the same starting point and one lies on top of the other.
Question 4.
Consider the case of \(\overline{C A}\) and \(\overline{C B}\)of lengths 5 and 12, respectively, with m∠C>180°.
a. Is the law of cosines consistent in being able to calculate the length of (AB) ̅ even using an angle this large? Try it for m∠C = 200°, and compare your results to the triangle with m∠C = 160°. Explain your findings.
Answer:
Yes, the law of cosines is still able to calculate the length of \(\overline{A B}\):
c2 = 52 + 122 – 2⋅5⋅12 cos(200°)
≈ 281.76
Thus, c ≈ 16.786, which represents the length of line segment AB. We get the same result for cos〖(160°)〗, which makes sense since it is true that cos(θ) = cos(360° – θ).
b. Consider what you have learned in Problems 1–4. If you were designing a computer program to be able to measure sides and angles of triangles created from different line segments and angles, would it make sense to use the law of cosines or several different techniques depending on the shape? Would a computer program created from the law of cosines have any errors based on different inputs for the line segments and angle between them?
Answer:
The benefits of using the law of cosines would be that there would be no need for logic involving different cases to be programmed, and there would be no exceptions to the formula. The law of cosines would work even when the shape formed was not a triangle or if the shape was formed using an angle greater than 180°. The triangle inequality theorem would need to be used to verify whether the side lengths could represent those of a triangle. There would be no errors for two line segments and the angle between them.
Question 5.
Consider triangles with the following measurements. If two sides are given, use the law of cosines to find the measure of the third side. If three sides are given, use the law of cosines to find the measure of the angle between a and b.
a. a = 4, b = 6, m∠C = 35°
Answer:
c ≈ 3.56
b. a = 2, b = 3, m∠C = 110°
Answer:
c ≈ 4.14
c. a = 5, b = 5, m∠C = 36°
Answer:
c ≈ 3.09
d. a = 7.5, b = 10, m∠C = 90°
Answer:
c ≈ 12.5
e. a = 4.4, b = 6.2, m∠C = 9°
Answer:
c ≈ 1.98
f. a = 12, b = 5, m∠C = 45°
Answer:
c ≈ 9.17
g. a = 3, b = 6, m∠C = 60°
Answer:
c ≈ 5.2
h. a = 4, b = 5, c = 6
Answer:
m∠C ≈ 82.82°
i. a = 1, b = 1, c = 1
Answer:
m∠C = 60°
j. a = 7, b = 8, c = 3
Answer:
m∠C ≈ 21.79°
k. a = 6, b = 5.5, c = 6.5
Answer:
m∠C ≈ 68.68°
l. a = 8, b = 5, c = 12
Answer:
m∠C ≈ 133.43°
m. a = 4.6, b = 9, c = 11.9
Answer:
m∠C ≈ 118.45°
Question 6.
A trebuchet launches a boulder at an angle of elevation of 33° at a force of 1,000 N. A strong gale wind is blowing against the boulder parallel to the ground at a force of 340 N. The figure is shown below.
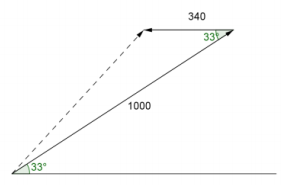
a. What is the force in the direction of the boulder’s path?
Answer:
Since the wind is blowing in the opposite direction, finding the sum of the two vectors is similar to finding the difference between two vectors if the wind is in the same direction. Thus, we are finding the third side of a triangle (the diagonal of the parallelogram).
c2 = 10002 + 3402 – 2⋅1000⋅340 cos(33°)
≈ 738.45
The boulder is traveling with an initial force of 738.45 N.
b. What is the angle of elevation of the boulder after the wind has influenced its path?
Answer:
The angle between the original trajectory and the new trajectory is 14.52°, so the new angle of elevation is 47.52°.
Question 7.
Cliff wants to build a tent for his son’s graduation party. The tent is a regular pentagon, as illustrated below. How much guy – wire (show in blue) does Cliff need to purchase to build this tent? Round your answers to the nearest thousandths.
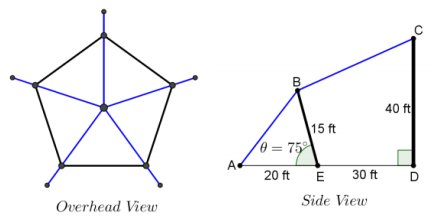
Answer:
AB = \(\sqrt{20^{2} + 15^{2} – 2 \cdot 20 \cdot 15 \cdot \cos \left(75^{\circ}\right)}\) ≈ 21.673
EC = \(\sqrt{40^{2} + 30^{2}}\) = 50
m∠CED = arctan(\(\frac{40}{30}\)) = 55.130°
m∠BEC = 180° – 75° – 55.130° = 49.870°
BC = \(\sqrt{15^{2} + 50^{2} – 2 \cdot 15 \cdot 50 \cdot \cos \left(49.870^{\circ}\right)}\) ≈ 41.931
AB + BC = 63.604
(5)(63.604) = 318.020
Total guy – wire is 318.020 feet long.
Question 8.
A roofing contractor needs to build roof trusses for a house. The side view of the truss is shown below. Given that G is the midpoint of \(\overline{A B}\), E is the midpoint of \(\overline{A G}\), I is the midpoint of \(\overline{G B}\), AB = 32 ft., AD = 6 ft., FC = 5 ft., and m∠AGC = 90°. Find DE, EF, and FG. Round your answers to the nearest thousandths.
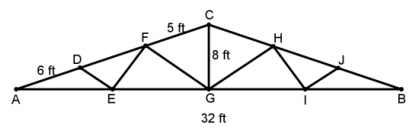
Answer:
m∠CAG = arctan(\(\frac{8}{16}\)) = 26.565°
DE = \(\sqrt{6^{2} + 8^{2} – 2 \cdot 6 \cdot 8 \cdot \cos \left(26.565^{\circ}\right)}\) ≈ 3.760
m∠ACG = 180° – 90° – 26.565° = 63.435°
FG = \(\sqrt{5^{2} + 8^{2} – 2 \cdot 5 \cdot 8 \cdot \cos \left(63.435^{\circ}\right)}\) ≈ 7.295
m∠FGC = arccos(\(\frac{8^{2} + 7.295^{2} – 5^{2}}{2 \cdot 8 \cdot 7.295}\)) ≈ 37.808°
m∠FGE = 90° – 37.808° = 52.192°
EF = \(\sqrt{8^{2} + 7.295^{2} – 2 \cdot 8 \cdot 7.295 \cdot \cos \left(52.192^{\circ}\right)}\) ≈ 6.758
DE is approximately 3.760 feet long, FG is approximately 7.295 feet long, and EF is approximately 6.758 feet long.
Eureka Math Precalculus Module 4 Lesson 9 Exit Ticket Answer Key
Use the law of cosines to solve the following problems.
Question 1.
Josie wishes to install a new television that will take up 15° of her vertical field of view. Using the angle she wants, she uses a laser measure and finds the distances from the wall to her couch are 8 ft. and 12 ft., but she does not have any way to mark the spots on the wall. How tall is the television that she wants?
Answer:
\(\sqrt{8^{2} + 12^{2} – 2 \cdot 8 \cdot 12 \cdot \cos \left(15^{\circ}\right)}\) ≈ 4.748
Josie’s television will be more than 4.748 ft. tall.
Question 2.
Given the figure shown, find the height of the evergreen tree. Round your answers to the nearest thousandths.
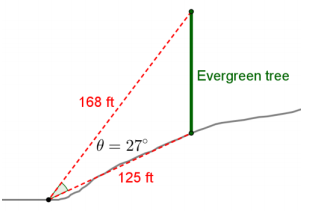
Answer:
\(\sqrt{125^{2} + 168^{2} – 2 \cdot 125 \cdot 168 \cdot \cos \left(27^{\circ}\right)}\) ≈ 80.167
The height of the tree is approximately 80.167 ft.