Engage NY Eureka Math Precalculus Module 4 Lesson 12 Answer Key
Eureka Math Precalculus Module 4 Lesson 12 Example Answer Key
Example 1.
Consider the function (x) = sin (x), –\(\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\).
a. State the domain and range of this function.
Answer:
D: –\(\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\)
R: -1 ≤ y ≤ 1
b. Find the equation of the inverse function.
Answer:
x = sin(y)
y = sin-1 (x)
c. State the domain and range of the inverse.
Answer:
D: -1 ≤ x ≤ 1
R: –\(\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
Example 2.
Solve each trigonometric equation such that 0 ≤ x ≤ 2π. Round to three decimal places when necessary.
a. 2 cos(x) – 1 = 0
Answer:
cos(x) = \(\frac{1}{2}\)
Reference angle: cos-1 (\(\frac{1}{2}\)) = \(\frac{\pi}{3}\)
The cosine function is positive in Quadrants I and IV.
x = \(\frac{\pi}{3}\) and \(\frac{5\pi}{3}\)
b. 3 sin(x) + 2 = 0
Answer:
sin(x) = –\(\frac{2}{3}\)
Reference angle: sin-1 (\(\frac{2}{3}\)) = 0.730
The sine function is negative in Quadrants III and IV.
x = π + 0.730 = 3.871 and x = 2π – 0.730 = 5.553
Eureka Math Precalculus Module 4 Lesson 12 Exercise Answer Key
Opening Exercise
Use the graphs of the sine, cosine, and tangent functions to answer each of the following questions.
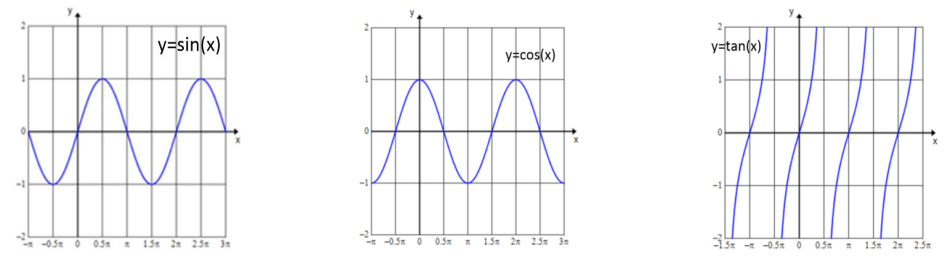
a. State the domain of each function.
Answer:
The domain of the sine and cosine functions is the set of all real numbers. The domain of the tangent function is the set of all real numbers x≠\(\frac{\pi}{2}\) + kπ for all integers k.
b. Would the inverse of the sine, cosine, or tangent functions also be functions? Explain.
Answer:
None of these functions are invertible. Multiple elements of the domain are paired with a single range element. When the domain and range are exchanged to form the inverse, the result does not satisfy the definition of a function.
c. For each function, select a suitable domain that will make the function invertible.
Answer:
Answers will vary, so share a variety of responses. Any answer is suitable as long as the restricted domain leaves an interval of the graph that is either always increasing or always decreasing.
Sample response:
y = sin (x), D:[0, \(\frac{\pi}{2}\)] y = cos (x), D:[0, π] y = tan(x), D:[0, \(\frac{\pi}{2}\)]
Exercises 1–3
Exercise 1.
Write an equation for the inverse cosine function, and state its domain and range.
Answer:
y = cos-1 (x)
D: -1 ≤ x ≤ 1
R: 0 ≤ y ≤ π
Exercise 2.
Write an equation for the inverse tangent function, and state its domain and range.
Answer:
y = tan-1 (x)
D: set of all real numbers
R: –\(\frac{\pi}{2}\)<y<\(\frac{\pi}{2}\)
Exercise 3.
Evaluate each of the following expressions without using a calculator. Use radian measures.
a. sin-1 (\(\frac{\sqrt{3}}{2}\))
Answer:
\(\frac{\pi}{3}\)
b. sin-1 (-\(\frac{\sqrt{3}}{2}\))
Answer:
–\(\frac{\pi}{3}\)
c. cos-1 (\(\frac{\sqrt{3}}{2}\))
Answer:
\(\frac{\pi}{6}\)
d. cos-1 (-\(\frac{\sqrt{3}}{2}\))
Answer:
\(\frac{5\pi}{6}\)
e. sin-1 (1)
Answer:
\(\frac{\pi}{2}\)
f. sin-1 (-1)
Answer:
–\(\frac{\pi}{2}\)
g. cos-1 (1)
Answer:
0
h. cos-1 (-1)
Answer:
π
i. tan-1 (1)
Answer:
\(\frac{\pi}{4}\)
j. tan-1 (-1)
Answer:
–\(\frac{\pi}{4}\)
Exercises 4–8
Exercise 4.
Solve each trigonometric equation such that 0 ≤ x ≤ 2π. Give answers in exact form.
a. \(\sqrt{2}\) cos(x) + 1 = 0
Answer:
x = \(\frac{3\pi}{4}\), \(\frac{5\pi}{4}\)
b. tan(x)-\(\sqrt{3}\) = 0
Answer:
x = \(\frac{\pi}{3}\), \(\frac{4\pi}{3}\)
c. sin2 (x) – 1 = 0
Answer:
x = \(\frac{\pi}{2}\), \(\frac{3\pi}{2}\)
Exercise 5.
Solve each trigonometric equation such that 0 ≤ x ≤ 2π. Round answers to three decimal places.
a. 5 cos(x) – 3 = 0
Answer:
x = 0.927, 5.356
b. 3 cos (x) + 5 = 0
Answer:
There are no solutions to this equation within the domain of the function.
c. 3 sin(x) – 1 = 0
Answer:
x = 0.340, 2.802
d. tan(x) = -0.115
Answer:
x = 3.027, 6.169
Exercise 6.
A particle is moving along a straight line for 0 ≤ t ≤ 18. The velocity of the particle at time t (in seconds) is given by the function v(t) = cos(\(\frac{\pi}{5}\) t). Find the time(s) on the interval 0 ≤ t ≤ 18 where the particle is at rest (v(t) = 0).
Answer:
The particle is at rest at t = 2.5 seconds, 7.5 seconds, 12.5 seconds, and 17.5 seconds.
Exercise 7.
In an amusement park, there is a small Ferris wheel, called a kiddie wheel, for toddlers. The formula H(t) = 10 sin(2π(t-\(\frac{1}{4}\))) + 15 models the height H (in feet) of the bottom-most car t minutes after the wheel begins to rotate. Once the ride starts, it lasts 4 minutes.
a. What is the initial height of the car?
Answer:
5 ft.
b. How long does it take for the wheel to make one full rotation?
Answer:
1 minute
c. What is the maximum height of the car?
Answer:
25 ft.
d. Find the time(s) on the interval 0 ≤ t ≤ 4 when the car is at its maximum height.
Answer:
The car is at its maximum height when sin(2π(t-\(\frac{1}{4}\))) = 1, which is at t = 0.5, 1.5, 2.5, and 3.5 minutes.
Exercise 8.
Many animal populations fluctuate periodically. Suppose that a wolf population over an 8-year period is given by the function W(t) = 800 sin(\(\frac{\pi}{4}\) t) + 2200, where t represents the number of years since the initial population counts were made.
a. Find the time(s) on the interval 0 ≤ t ≤ 8 such that the wolf population equals 2, 500.
Answer:
t = 0.489, 3.511
The wolf population equals 2, 500 after approximately 0.5 years and again after 3.5 years.
b. On what time interval during the 8-year period is the population below 2, 000?
Answer:
W(t) = 2000 at t = 4.332 and 7.678
The wolf population is below 2, 000 on the time interval (4.332, 7.678).
c. Why would an animal population be an example of a periodic phenomenon?
Answer:
An animal population might increase while their food source is plentiful. Then, when the population becomes too large, there is less food and the population begins to decrease. At a certain point, there are few enough animals that there is plenty of food for the entire population at which point the population begins to increase again.
Eureka Math Precalculus Module 4 Lesson 12 Problem Set Answer Key
Question 1.
Solve the following equations. Approximate values of the inverse trigonometric functions to the thousandths place, where x refers to an angle measured in radians.
a. 5 = 6 cos(x)
Answer:
2πk ± 0.586
b. –\(\frac{1}{2}\) = 2 cos(x-\(\frac{\pi}{4}\)) + 1
Answer:
2πk + \(\frac{5\pi}{4}\)-0.723
2πk – \(\frac{3\pi}{4}\) + 0.723
c. 1 = cos(3(x – 1))
Answer:
\(\frac{2 \pi k}{3}\) + 1
d. 1.2 = -0.5 cos(πx) + 0.9
Answer:
\(\frac{-0.927 + \pi + 2 \pi k}{\pi}\)
\(\frac{0.927-\pi + 2 \pi k}{\pi}\)
e. 7 = -9 cos(x) – 4
Answer:
No solutions
f. 2 = 3 sin(x)
Answer:
0.730 + 2πk
π-0.730 + 2πk
g. -1 = sin(\(\frac{\pi(x-1)}{4}\))-1
Answer:
4k + 1
h. π = 3 sin(5x + 2) + 2
Answer:
\(\frac{0.390-2 + 2 \pi k}{5}\)
\(\frac{\pi-0.390-2 + 2 \pi k}{5}\)
i. \(\frac{1}{9}\) = \(\frac{\sin (x)}{4}\)
Answer:
0.461 + 2πk
π-0.461 + 2πk
j. cos(x) = sin(x)
1 = \(\frac{\sin (x)}{\cos (x)}\) = tan(x)
\(\frac{\pi}{4}\) + πk (or 0.785 + πk)
k. sin-1(cos(x) ) = \(\frac{\pi}{3}\)
Answer:
2πk ± \(\frac{\pi}{6}\)
l. tan(x) = 3
Answer:
1.249 + πk
m. -1 = 2 tan(5x + 2)-3
Answer:
\(\frac{\frac{\pi}{4}-2 + \pi k}{5}\)
Alternatively, \(\frac{0.785-2 + \pi k}{5}\).
n. 5 = -1.5 tan(-x)-3
Answer:
1.385 + πk
Question 2.
Fill out the following tables.
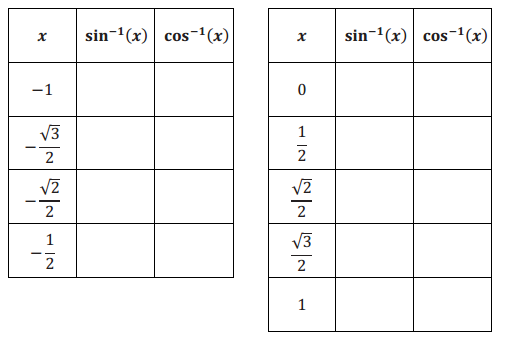
Answer:
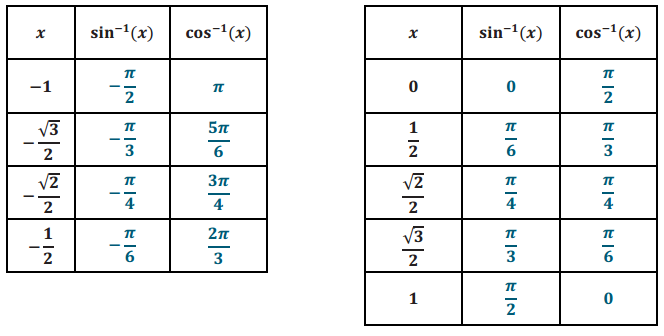
Question 3.
Let the velocity v in miles per second of a particle in a particle accelerator after t seconds be modeled by the function v = tan(\(\frac{\pi t}{6000}-\frac{\pi}{2}\)) on an unknown domain.
a. What is the t-value of the first vertical asymptote to the right of the y-axis?
Answer:
t = 6000
b. If the particle accelerates to 99% of the speed of light before stopping, then what is the domain?
Answer:
Note: c ≈ 186, 000. Round your solution to the ten-thousandths place.
0.99 ⋅ 186 000 = 184 140
184 140 = tan(\(\frac{\pi t}{6000}-\frac{\pi}{2}\))
tan-1(184 140) = \(\frac{\pi t}{6000}-\frac{\pi}{2}\)
\(\frac{6000}{\pi}\) ⋅ (tan-1(184 140) + \(\frac{\pi}{2}\)) = t
t ≈ 5999.9896
So the domain is 0 < t ≤ 5999.9896.
c. How close does the domain get to the vertical asymptote of the function?
Answer:
Very close. They are only different at the hundredths place.
d. How long does it take for the particle to reach the velocity of Earth around the sun (about 18.5 miles per second)?
Answer:
18.5 = tan(\(\frac{\pi t}{6000}-\frac{\pi}{2}\))
tan-1(18.5) = \(\frac{\pi t}{6000}-\frac{\pi}{2}\)
\(\frac{6000}{\pi}\) ⋅ (tan-1(18.5) + \(\frac{\pi}{2}\)) = t
t ≈ 5896.864
It takes approximately 5, 896.864 seconds to reach the velocity of Earth around the sun.
e. What does it imply that v is negative up until t = 3000?
Answer:
The particle is traveling in the opposite direction.
Eureka Math Precalculus Module 4 Lesson 12 Exit Ticket Answer Key
Question 1.
State the domain and range for f(x) = sin-1(x), g(x) = cos-1(x), and h(x) = tan-1(x).
Answer:
For f, the domain is all real numbers x, such that -1 ≤ x ≤ 1, and the range is all real numbers y, such that
–\(\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\).
For g, the domain is all real numbers x, such that -1 ≤ x ≤ 1, and the range is all real numbers y, such that
0 ≤ y ≤ π.
For h, the domain is all real numbers x, and the range is all real numbers y, such that –\(\frac{\pi}{2}\)<y<\(\frac{\pi}{2}\).
Question 2.
Solve each trigonometric equation such that 0 ≤ x ≤ 2π. Give answers in exact form.
a. 2 sin(x) + \(\sqrt{3}\) = 0
Answer:
x = \(\frac{4\pi}{3}\), \(\frac{5\pi}{3}\)
b. tan2(x)-1 = 0
Answer:
x = \(\frac{\pi}{4}\), \(\frac{3\pi}{4}\), \(\frac{5\pi}{4}\), \(7\frac{\pi}{4}\)
Question 3.
Solve the trigonometric equation such that 0 ≤ x ≤ 2π. Round to three decimal places.
\(\sqrt{5}\) cos(x)-2 = 0
Answer:
x = 0.464, 5.819