Engage NY Eureka Math Precalculus Module 3 Lesson 5 Answer Key
Eureka Math Precalculus Module 3 Lesson 5 Example Answer Key
Example 1.
Look at the alternating sums of the rows of Pascal’s triangle. An alternating sum alternately subtracts and then adds values. For example, the alternating sum of Row 2 would be 1 – 2 + 1, and the alternating sum of Row 3 would be
1 – 3 + 3 – 1.
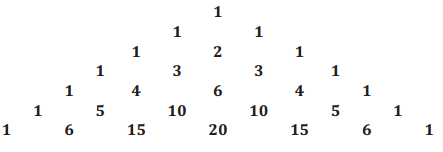
a. Compute the alternating sum for each row of the triangle shown.
Answer:
The sums are all zero.
b. Use the binomial theorem to explain why each alternating sum of a row in Pascal’s triangle is 0.
Answer:
The binomial theorem states that (u + v)n = un + A1 u(n – 1) v + A2 u(n – 2) v2 + A(n – 1) uv(n – 1) + n.
So, 0 = (1 + ( – 1))n = 1n + A1(1(n – 1))( – 1) + A2(1(n – 2))( – 1)2 + ⋯ + A(n – 1) (1)( – 1)(n – 1) + ( – 1)n = 1 – A1 + A2 + ⋯ – A(n – 1) + 1 for all even values of n or 1 – A1 + A2 + ⋯ + A(n – 1) – 1 for all odd values of n.
Example 2.
We know that the volume V(r) and surface area S(r) of a sphere of radius r are given by these formulas:
V(r) = \(\frac{4}{3}\) πr3
S(r) = 4πr2
Suppose we increase the radius of a sphere by 0.01 units from r to r + 0.01.
a. Use the binomial theorem to write an expression for the increase in volume.
Answer:
V(r + 0.01) – V(r) = \(\frac{4}{3}\) π(r + 0.01)3 – \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π((r)3 + 3(r)2 (0.01) + 3r(0.01)2 + (0.01)3) – \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) πr3 + 0.04π(r)2 + 0.0004πr + 0.000 001π – \(\frac{4}{3}\) πr3
= 0.04π(r)2 + 0.0004πr + 0.000 001π
b. Write an expression for the average rate of change of the volume as the radius increases from r to r + 0.01.
Answer:
Average rate of change = \(\frac{V(r + 0.01) – V(r)}{(r + 0.01) – r}\)
c. Simplify the expression in part (b) to compute the average rate of change of the volume of a sphere as the radius increases from r to r + 0.01.
Answer:
Average rate of change = \(\frac{0.04 \pi(r)^{2} + 0.0004 \pi r + 0.000001 \pi}{0.01}\) = 4πr2 + 0.04πr + 0.0001π
d. What does the expression from part (c) resemble?
Answer:
Surface area of the sphere with radius r
e. Why does it make sense that the average rate of change should approximate the surface area? Think about the geometric figure formed by V(r + 0.01) – V(r). What does this represent?
Answer:
It is a shell of volume, a layer 0.01 units thick, covering the surface area of the inner sphere of radius r.
f. How could we approximate the volume of the shell using surface area? And the average rate of change for the volume?
Answer:
The volume is approximately S(r)⋅(0.01); rate of change of volume is approximately \(\frac{S(r) \times 0.01}{0.01}\) = S(r), which is the surface area of the sphere, S(r).
Eureka Math Precalculus Module 3 Lesson 5 Exercise Answer Key
Opening Exercise
Write the first six rows of Pascal’s triangle. Then, use the triangle to find the coefficients of the terms with the powers of u and v shown, assuming that all expansions are in the form (u + v)n. Explain how Pascal’s triangle allows you to determine the coefficient.
Answer:

a. u2 v4
Answer:
15; this is in Row 6 (sum of exponents is 6) and the fifth term since the power of u started at 6 and has decreased to 2, which takes 5 steps.
b. u3 v2
Answer:
10; this is the third term in Row 5.
c. u2 v2
Answer:
6; this is the third term in Row 4.
d. v10
Answer:
1; this is the last term in Row 10 since there is no u.
Exercises 1–2
Exercise 1.
Consider Rows 0–6 of Pascal’s triangle.
a. Find the sum of each row.
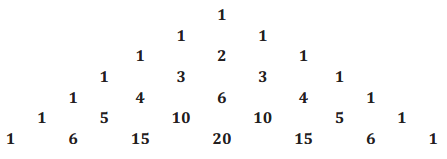
Answer:
SUM
1
2
4
8
16
32
64
b. What pattern do you notice in the sums computed?
Answer:
The sum of the coefficients in the nth row appears to be 2n.
c. Use the binomial theorem to explain this pattern.
Answer:
2n = (1 + 1)n
The binomial theorem states that (u + v)n = un + A1 un – 1 v + A2 un – 2 v2 + ⋯ + An – 1 uvn – 1 + vn.
So,
(1 + 1)n = 1n + A1 (1n – 1)(1) + A2 (1n – 2)(1)2 + ⋯ + An – 1 (1)(1)n – 1 + 1n = 1 + A1 + A2 + ⋯ + An – 1 + 1, which is the sum of the coefficients of the nth row of Pascal’s triangle.
Exercise 2.
Consider the expression 11n.
a. Calculate 11n, where n = 0, 1, 2, 3, 4.
Answer:
110 = 1
111 = 11
112 = 121
113 = 1331
114 = 14641
b. What pattern do you notice in the successive powers?
Answer:
The digits of 11n correspond to the coefficients in the nth row of Pascal’s triangle.
c. Use the binomial theorem to demonstrate why this pattern arises.
Answer:
11n = (10 + 1)n = 10n + A1 (10)n – 1 (1) + A2 (10)n – 2 (1)2 + ⋯ + An – 1 (10)(1)n – 1 + 1n
= 10n + A1 (10)n – 1 + A2 (10)n – 2 + ⋯ + An – 1 (10) + 1
d. Use a calculator to find the value of 115. Explain whether this value represents what would be expected based on the pattern seen in lower powers of 11.
Answer:
If we continued the pattern seen in 11n, where n = 0, 1, 2, 3, 4, we would expect 115 to comprise the digits of the fifth row in Pascal’s triangle. In other words, we could conjecture that 115 = 1|5|10|10|5|1. Because we cannot represent a 10 as a single digit, the number on the calculator would be 161,051.
Eureka Math Precalculus Module 3 Lesson 5 Problem Set Answer Key
Question 1.
Consider the binomial (2u – 3v)6.
a. Find the term that contains v4.
Answer:
15(2u)2 (3v)4 = 4860u2 v4
b. Find the term that contains u3.
Answer:
20(2u)3 (3v)3 = 4320u3 v3
c. Find the third term.
Answer:
15(2u)4 (3v)2 = 2160u4 v2
Question 2.
Consider the binomial (u2 – v3)6.
a. Find the term that contains v6.
Answer:
v6 = (v3)2, 15(u2)4 (v3)2 = 15u^8 v6
b. Find the term that contains u6.
Answer:
u6 = (u2)3, 20(u2)3(v3)3 = 20u6 v9
c. Find the fifth term.
Answer:
15(u2)2 (v3)4 = 15u4 v12
Question 3.
Find the sum of all coefficients in the following binomial expansion.
a. (2u + v)10
Answer:
310 = 59049
b. (2u – v)10
Answer:
1
c. (2u – 3v)11
Answer:
– 1
d. (u – 3v)11
Answer:
– 211
e. (1 + i)10
Answer:
((1 + i)2)5 = (1 + 2i – 1)5 = (2i)5 = 32i
f. (1 – i)10
Answer:
((1 – i)2)5 = (1 – 2i – 1)5 = ( – 2i)5 = – 32i
g. (1 + i)200
Answer:
((1 + i)2)100 = (1 + 2i – 1)100 = (2i)100 = 2100
h. (1 + i)201
Answer:
(1 + i) (1 + i)200 = (1 + i)((1 + i)2)100 = (1 + i)2100
Question 4.
Expand the binomial (1 + \(\sqrt{2}\)i)6.
Answer:
1 + 6(1)5 (\(\sqrt{2}\)i) + 15(1)4 (\(\sqrt{2}\)i)2 + 20(1)3(\(\sqrt{2}\)i)3 + 15(1)2 (\(\sqrt{2}\)i)4 + 6(1) (\(\sqrt{2}\)i)5 + (\(\sqrt{2}\)i)6
1 + 6\(\sqrt{2}\)i – 30 – 40\(\sqrt{2}\)i + 60 + 24\(\sqrt{2}\)i – 8 = 23 – 10\(\sqrt{2}\)i
Question 5.
Show that (2 + \(\sqrt{2}\)i)20 + (2 – \(\sqrt{2}\)i)20 is an integer.
Answer:
Let’s get the first few terms for both to see whether it has any patterns that we can simplify.
(2 + \(\sqrt{2}\)i)2 = 220 + A1 (2)19 (\(\sqrt{2}\)i)1 + A2 (2)18(\(\sqrt{2}\)i)2 + A3 (2)17 (\(\sqrt{2}\)i)3 + A4 (2)18(\(\sqrt{2}\)i)4 + A5 (2)18(\(\sqrt{2}\)i)5 + ⋯ – A17 (2)3 (\(\sqrt{2}\)i)17 + A18 (2)2 (\(\sqrt{2}\)i)18 + A19 (2)1 (\(\sqrt{2}\)i)19 + (\(\sqrt{2}\)i)20
(2 – \(\sqrt{2}\)i)2 = 220 – A1 (2)19 (\(\sqrt{2}\)i)1 + A2 (2)18(\(\sqrt{2}\)i)2 – A3 (2)17 (\(\sqrt{2}\)i)3 + A4 (2)18(\(\sqrt{2}\)i)4 + A5 (2)18(\(\sqrt{2}\)i)5 + ⋯ – A17 (2)3 (\(\sqrt{2}\)i)17 + A18 (2)2 (\(\sqrt{2}\)i)18 – A19 (2)1 (\(\sqrt{2}\)i)19 + (\(\sqrt{2}\)i)20
All the even terms are canceled, and the remaining terms would involve multiplying powers of 2 with even powers of \(\sqrt{2}\). So, the result would be the sum of some positive and negative integers, which is 116,967,424.
Question 6.
We know (u + v)2 = u2 + 2uv + v2 = u2 + v2 + 2uv. Use this pattern to predict what the expanded form of each expression would be. Then, expand the expression, and compare your results.
a. (u + v + w)2
Answer:
u2 + v2 + w2 + 2uv + 2uw + 2vw
b. (a + b + c + d)2
Answer:
a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
Question 7.
Look at the powers of 101 up to the fourth power on a calculator. Explain what you see. Predict the value of 1015, and then find the answer on a calculator. Are they the same?
Answer:

It is similar to Pascal’s triangle, but zeros are inserted between the numbers in each row. The answers are not the same; the expanded form of 1|0|5|0|10|0|10|0|5|0|1 is 10, 510, 100, 501; however, if we could represent a 10 as a single digit in our base – ten arithmetic, then both answers would be the same.
Question 8.
Can Pascal’s triangle be applied to (\(\frac{1}{u}\) + \(\frac{1}{v}\))n given u,v≠0?
Answer:
Yes. The answer is (\(\frac{1}{u}\) + \(\frac{1}{v}\))n = \(\frac{1}{u^{n}}\) + \(\frac{A_{1}}{u^{(n – 1)} v}\)) + \(\frac{A_{2}}{u^{(n – 2)} v^{2}}\) + ⋯ + \(\frac{A_{n – 2}}{u^{2} v^{(n – 2)}}\) + \(\frac{A_{n – 1}}{u v^{(n – 1)}}\) + \(\frac{1}{v^{n}}\) .
Question 9.
The volume and surface area of a sphere are given by V = \(\frac{4}{3}\) πr3 and S = 4πr2. Suppose we increase the radius of a sphere by 0.001 units from r to r + 0.001.
a. Use the binomial theorem to write an expression for the increase in volume V(r + 0.001) – V(r) as the sum of three terms.
Answer:
V(r + 0.001) – V(r) = \(\frac{4}{3}\) π(r + 0.001)3 – \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π[(r)3 + 3(r)2 (0.001) + 3r(0.001)2 + (0.001)3 ] – \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) πr3 + 0.004π(r)2 + 0.000 004πr + \(\frac{0.000000004 \pi}{3}\) – \(\frac{4}{3}\) πr3
= 0.004π(r)2 + 0.000 004πr + \(\frac{0.000000004 \pi}{3}\)
b. Write an expression for the average rate of change of the volume as the radius increases from r to r + 0.001.
Answer:
Average rate of change: \(\frac{V(r + 0.001) – V(r)}{(r + 0.001) – r}\)
c. Simplify the expression in part (b) to compute the average rate of change of the volume of a sphere as the radius increases from r to r + 0.001.
Answer:
Average rate of change: \(\frac{0.004 \pi(r)^{2} + 0.000004 \pi r + \frac{0.000000004 \pi}{3}}{0.001}\) = 4πr2 + 0.004πr + 0.000 004π
d. What does the expression from part (c) resemble?
Answer:
Surface area of the sphere with radius r
e. Why does it make sense that the average rate of change should approximate the surface area? Think about the geometric figure formed by V(r + 0.001) – V(r). What does this represent?
Answer:
It is a shell of the volume, a layer 0.001 units thick, covering the surface area of the inner sphere of radius r.
f. How could we approximate the volume of the shell using surface area? And the average rate of change for the volume?
Answer:
The volume is approximately S(r)⋅0.001; the rate of change of volume is approximately \(\frac{s(r) \times 0.001}{0.001}\), which is the surface area of the sphere, S(r).
g. Find the difference between the average rate of change of the volume and S(r) when r = 1.
Answer:
Average rate of change = 4π(1)2 + 0.004π(1) + 0.000 004π = 12.579
S(1) = 4π(1)2 = 12.566
12.579 – 12.566 = 0.013
Question 10.
The area and circumference of a circle of radius r are given by A(r) = πr2 and C(r) = 2πr. Suppose we increase the radius of a sphere by 0.001 units from r to r + 0.001.
a. Use the binomial theorem to write an expression for the increase in area volume A(r + 0.001) – A(r) as a sum of three terms.
Answer:
A(r + 0.001) – V(r) = π(r + 0.001)2 – πr2
= πr2 + 0.002πr + 0.000 001π – πr2
= 0.002πr + 0.000 001π
b. Write an expression for the average rate of change of the area as the radius increases from r to r + 0.001.
Answer:
Average rate of change: \(\frac{A(r + 0.001) – A(r)}{(r + 0.001) – r}\)
c. Simplify the expression in part (b) to compute the average rate of change of the area of a circle as the radius increases from r to r + 0.001.
Answer:
Average rate of change: \(\frac{0.002 \pi r + 0.000001 \pi}{0.001}\) = 2πr + 0.001π
d. What does the expression from part (c) resemble?
Answer:
Surface area of the circle with radius r
e. Why does it make sense that the average rate of change should approximate the area of a circle? Think about the geometric figure formed by A(r + 0.001) – A(r). What does this represent?
Answer:
It is a shell of the volume, a layer 0.01 units thick, covering the surface area of the inner circle of radius r.
f. How could we approximate the area of the shell using circumference? And the average rate of change for the area?
Answer:
The volume is approximately A(s)⋅0.001; rate of change of volume is approximately \(\frac{A(s) \times 0.001}{0.001}\), which is the surface area of the circle, A(s).
g. Find the difference between the average rate of change of the area and C(r) when r = 1.
Answer:
Average rate of change = 2π(1) + 0.001(1) = 6.284
C(1) = 2π(1) = 6.283
6.284 – 6.283 = 0.001
Eureka Math Precalculus Module 3 Lesson 5 Exit Ticket Answer Key
Question 1.
The area and circumference of a circle of radius r are given by
A(r) = πr2
C(r) = 2πr
a. Show mathematically that the average rate of change of the area of the circle as the radius increases from r to r + 0.01 units is very close to the circumference of the circle.
Answer:
Average rate of change: (A(r + 0.01) – A(r))/((r + 0.01) – r)
A(r + 0.01) – A(r) = π(r + 0.01)2 – πr2
= πr2 + 2π(r)(0.01) + π(0.01)2 – πr2
= 0.02πr + 0.0001π
Average rate of change: \(\frac{0.02 \pi r + 0.0001 \pi}{0.01}\) = 2πr + 0.01π, which is approximately equal to C(r).
b. Explain why this makes sense geometrically.
Answer:
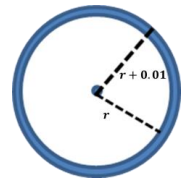
The difference A(r + 0.01) – A(r) represents the area of a ring of width 0.01 units, where the inner circle forming the ring is a circle with radius r. The area of the ring could be approximated by the expression
0.01⋅2πr. The average rate of change of the area is \(\frac{0.01 \cdot 2 \pi r}{0.01}\) = 2πr, which is the circumference of the circle with radius r.