Engage NY Eureka Math Precalculus Module 3 Lesson 1 Answer Key
Eureka Math Precalculus Module 3 Lesson 1 Example Answer Key
Example 1: Prove that a Quadratic Equation Has Only Two Solutions over the Set of Complex Numbers
Prove that 1 and – 1 are the only solutions to the equation x2 = 1.
Let x = a + bi be a complex number so that x2 = 1.
a. Substitute a + bi for x in the equation x2 = 1.
Answer:
(a + bi)2 = 1
b. Rewrite both sides in standard form for a complex number.
Answer:
a2 + 2abi + b2 i2 = 1
(a2 – b2 ) + 2abi = 1 + 0i
c. Equate the real parts on each side of the equation and equate the imaginary parts on each side of the equation.
Answer:
a2 – b2 = 1 and 2ab = 0
d. Solve for a and b, and find the solutions for x = a + bi.
Answer:
For 2ab = 0, either a = 0 or b = 0.
If a = 0, then – b2 = 1, which gives us b = i or b = – i.
Substituting into x = a + bi gives us 0 + i∙i = – 1 or 0 – i∙i = 1.
If b = 0, then a2 = 1, which gives us a = 1 or a = – 1.
Substituting into x = a + bi gives us 1 + 0∙i = 1 or – 1 + 0∙i = – 1.
Thus, the only complex number solutions to this equation are the complex numbers 1 + 0i or – 1 + 0i.
Eureka Math Precalculus Module 3 Lesson 1 Exercise Answer Key
Opening Exercise
How many solutions are there to the equation x2 = 1? Explain how you know.
Answer:
There are two solutions to the equation: 1 and – 1. I know these are the solutions because they make the equation true when each value is substituted for x.
Exercises
Find the product.
Exercise 1.
(z – 2)(z + 2)
Answer:
z2 – 4
Exercise 2.
(z + 3i)(z – 3i)
Answer:
z2 + 9
Write each of the following quadratic expressions as the product of two linear factors.
Exercise 3.
z2 – 4
Answer:
(z + 2)(z – 2)
Exercise 4.
z2 + 4
Answer:
(z + 2i)(z – 2i)
Exercise 5.
z2 – 4i
Answer:
(z + 2√i)(z – 2\(\sqrt{i}\)) or (z + (1 + i) \(\sqrt{2}\))(z – (1 + i) \(\sqrt{2}\)) [using the fact that \(\sqrt{i}\) = \( = \frac{1 + i}{\sqrt{2}}\)]
Exercise 6.
z2 + 4i
Answer:
(z + 2i\(\sqrt{i}\))(z – 2i\(\sqrt{i}\)) or (z + (i – 1) \(\sqrt{2}\))(z – (i – 1) \(\sqrt{2}\)) [using the fact that \(\sqrt{i}\) = \(\frac{1 + i}{\sqrt{2}}\)
Exercise 7.
Can a quadratic polynomial equation with real coefficients have one real solution and one complex solution? If so, give an example of such an equation. If not, explain why not.
Answer:
The quadratic formula shows that if the discriminant b2 – 4ac is negative, both solutions are complex numbers that are complex conjugates. If it is positive, both solutions are real. If it is zero, there is one (repeated) real solution. We cannot have a real solution coupled with a complex solution because complex solutions occur in conjugate pairs.
Recall from Algebra II that every quadratic expression can be written as a product of two linear factors, that is,
ax2 + bx + c = a(x – r1)(x – r2),
where r1 and r2 are solutions of the polynomial equation ax2 + bx + c = 0.
Exercise 8.
Solve each equation by factoring, and state the solutions.
a. x2 + 25 = 0
Answer:
(x + 5i)(x – 5i) = 0
The solutions are 5i and – 5i.
b. x2 + 10x + 25 = 0
Answer:
(x + 5)(x + 5) = 0
The solution is – 5.
Exercise 9.
Give an example of a quadratic equation with 2 + 3i as one of its solutions.
Answer:
We know that if 2 + 3i is a solution of the equation, then its conjugate 2 – 3i must also be a solution.
(x – (2 + 3i))(x – (2 – 3i)) = ((x – 2) – 3i)((x – 2) + 3i)
Using the structure of this expression, we have (a – bi)(a + bi) where a = x – 2 and b = 3.
Since (a + bi)(a – bi) = a2 + b2 for all real numbers a and b,
(x – 2 – 3i)(x – 2 + 3i) = (x – 2)2 + 33
= x2 – 4x + 4 + 9
= x2 – 4x + 13.
Exercise 10.
A quadratic polynomial equation with real coefficients has a complex solution of the form a + bi with b≠0. What must its other solution be and why?
Answer:
The other solution is a – bi. If the polynomial equation must have real coefficients, then
(x – (a + bi))(x – (a – bi)) when multiplied must yield an expression with real number coefficients.
(x – (a + bi))(x – (a – bi)) = (x – a – bi)(x – a + bi)
= (x – a)2 – b2 i2
= (x – a)2 + b2
= x2 – 2ax + a2 + b2
Since a and b are real numbers, this expression always has real number coefficients.
Exercise 11.
Write the left side of each equation as a product of linear factors, and state the solutions.
a. x3 – 1 = 0
Answer:
0 = x3 – 1 = (x – 1)(x2 + x + 1)
Using the quadratic formula, x = \(\frac{ – 1 \pm \sqrt{1 – 4}}{2}\) = \(\frac{ – 1 \pm i \sqrt{3}}{2}\), so the quadratic expression x2 + x + 1 factors into
x2 + x + 1 = (x – (\(\frac{ – 1 + i \sqrt{3}}{2}\)))(x – (\(\frac{ – 1 – i \sqrt{3}}{2}\))).
Then, the factored form of the equation is
(x – 1)(x – (\(\frac{ – 1 + i \sqrt{3}}{2}\)))(x – (\(\frac{ – 1 – i \sqrt{3}}{2}\)) = 0.
The solutions are 1, \(\frac{ – 1 + i \sqrt{3}}{2}\), and \(\frac{ – 1 – i \sqrt{3}}{2}\).
b. x3 + 8 = 0
Answer:
x3 + 8 = (x + 2)(x2 – 2x + 4)
Using the quadratic formula, x = \(\frac{2 \pm \sqrt{4 – 16}}{2}\) = \(\frac{2 \pm \sqrt{ – 12}}{2}\) = \(\frac{2 \pm 2 \sqrt{ – 3}}{2}\) = 1±i\(\sqrt{3}\), so the quadratic expression
x2 – 2x + 4 factors into
x2±2 + 4 = (x – (1 + i\(\sqrt{3}\)))(x – (1 – i\(\sqrt{3}\))).
Then, the factored form of the equation is
(x + 2)(x – (1 + i\(\sqrt{3}\)))(x – (1 – i\(\sqrt{3}\))) = 0.
The solutions are – 2, 1 + i \(\sqrt{3}\), and 1 – i\(\sqrt{3}\).
c. x4 + 7x2 + 10 = 0
Answer:
(x2 + 5)(x2 + 2) = (x + i\(\sqrt{5}\))(x – i\(\sqrt{5}\))(x + i\(\sqrt{2}\))(x – i\(\sqrt{2}\)) = 0
The solutions are ±i\(\sqrt{5}\) and ±i\(\sqrt{2}\).
Exercise 12.
Consider the polynomial p(x) = x3 + 4x2 + 6x – 36.
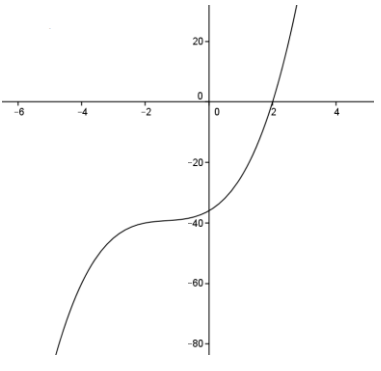
a. Graph y = x3 + 4x2 + 6x – 36, and find the real zero of polynomial p.
Answer:
The graph of p has an x – intercept at x = 2. Therefore, x = 2 is a zero of p.
b. Write p as a product of linear factors.
Answer:
p(x) = (x – 2)(x + 3 – 3i)(x + 3 + 3i)
c. What are the solutions to the equation p(x) = 0?
Answer:
The solutions are 2, – 3 + 3i, and – 3 – 3i.
Exercise 13.
Malaya was told that the volume of a box that is a cube is 4,096 cubic inches. She knows the formula for the volume of a cube with side length x is V(x) = x3, so she models the volume of the box with the equation
x3 – 4096 = 0.
a. Solve this equation for x.
Answer:
x3 – 4096 = (x – 16)(x2 + 16x + 256) = 0
x = 16, x = – 8 + 8\(\sqrt{3}\) i, x = – 8 – 8\(\sqrt{3}\) i
b. Malaya shows her work to Tiffany and tells her that she has found three different values for the side length of the box. Tiffany looks over Malaya’s work and sees that it is correct but explains to her that there is only one valid answer. Help Tiffany explain which answer is valid and why.
Answer:
Since we are looking for the dimensions of a box, only real solutions are acceptable, so the answer is
16 inches.
Exercise 14.
Consider the polynomial p(x) = x6 – 2x5 + 7x4 – 10x3 + 14x2 – 8x + 8.
a. Graph y = x6 – 2x5 + 7x4 – 10x3 + 14x2 – 8x + 8, and state the number of real zeros of p.
Answer:
There are no real zeros.
b. Verify that i is a zero of p.
Answer:
p(i) = i6 – 2i5 + 7i4 – 10i3 + 14i2 – 8i + 8
= – 1 – 2i + 7 + 10i – 14 – 8i + 8
= 0
c. Given that i is a zero of p, state another zero of p.
Answer:
Another zero is – i.
d. Given that 2i and 1 + i are also zeros of p, explain why polynomial p cannot possibly have any real zeros.
Answer:
Since 2i and 1 + i are zeros, – 2i and 1 – i must also be zeros of p. The fundamental theorem of algebra tells us that since p is a degree – 6 polynomial it can be written as a product of 6 linear factors. We now know that p has 6 complex zeros and therefore cannot have any real zeros.
e. What is the solution set to the equation p(x) = 0?
Answer:
The solution set is {i, – i,2i, – 2i,1 + i,1 – i}.
Exercise 15.
Think of an example of a sixth – degree polynomial equation that, when written in standard form, has integer coefficients, four real number solutions, and two imaginary number solutions. How can you be sure your equation will have integer coefficients?
Answer:
One correct response is (x – 1)(x + 1)(x – 2)(x + 2)(x – 2i)(x + 2i) = 0. By selecting an imaginary number bi, where b is an integer, and its conjugate as solutions, we know by the identity (a + bi)(a – bi) = a2 + b2 that these factors produce a quadratic expression with integer coefficients. If we choose the real solutions to also be integers, then, when written in standard form, the polynomial equation has integer coefficients.
Eureka Math Precalculus Module 3 Lesson 1 Problem Set Answer Key
Question 1.
Find all solutions to the following quadratic equations, and write each equation in factored form.
a. x2 + 25 = 0
Answer:
x = ±5i,
(x + 5i)(x – 5i) = 0
b. – x2 – 16 = – 7
Answer:
x = ±3i,
(x + 3i)(x – 3i) = 0
c. (x + 2)2 + 1 = 0
Answer:
x2 + 4x + 5 = 0, x = \(\frac{ – 4 \pm \sqrt{16 – 20}}{2}\) = \(\frac{ – 4 \pm 2 i}{2}\) = – 2±i
(x + 2 + i)(x + 2 – i) = 0
d. (x + 2)2 = x
Answer:
x2 + 3x + 4 = 0, x = \(\frac{ – 3 \pm \sqrt{9 – 16}}{2}\) = \(\frac{ – 3 \pm \sqrt{3} i}{2}\) = – \(\frac{3}{2}\)±\(\frac{\sqrt{3} i}{2}\)
(x + \(\frac{3}{2}\) + \(\frac{\sqrt{3} i}{2}\))(x + \(\frac{3}{2}\) – \(\frac{\sqrt{3} i}{2}\)) = 0
e. (x2 + 1)2 + 2(x2 + 1) – 8 = 0
Answer:
(x2 + 1 + 4)(x2 + 1 – 2) = 0, x2 + 5 = 0, x = ±\(\sqrt{5}\)i, x2 – 1 = 0, x = ±1
(x + \(\sqrt{5}\)i)(x – \(\sqrt{5}\)i)(x + 1)(x – 1) = 0
f. (2x – 1)2 = (x + 1)2 – 3
Answer:
4x2 – 4x + 1 – x2 – 2x – 1 + 3 = 0, 3x2 – 6x + 3 = 0, x2 – 2x + 1 = 0,
(x – 1)2 = 0, x = ±1
(x + 1)(x – 1) = 0
g. x3 + x2 – 2x = 0
Answer:
x(x2 + x – 2) = 0, x(x + 2)(x – 1) = 0,
x = 0, x = – 2, x = 1
x(x + 2)(x – 1) = 0
h. x3 – 2x2 + 4x – 8 = 0
Answer:
x2 (x – 2) + 4(x – 2) = 0, (x – 2)(x2 + 4) = 0, x = 2, x = ±2i
(x – 2)(x + 2i)(x – 2i) = 0
Question 2.
The following cubic equations all have at least one real solution. Find the remaining solutions.
a. x3 – 2x2 – 5x + 6 = 0
Answer:
One real solution is – 2; then x3 – 2x2 – 5x + 6 = (x + 2)(x2 – 4x + 3) = (x + 2)(x – 1)(x – 3).
The solutions are – 2, 1, 3.
b. x3 – 4x2 + 6x – 4 = 0
Answer:
One real solution is 2; then x3 – 4x2 + 6x – 4 = (x – 2)(x2 – 2x + 2). Using the quadratic formula on x2 – 2x + 2 = 0 gives x = 1±i.
The solutions are 2, 1 + i, 1 – i.
c. x3 + x2 + 9x + 9 = 0
Answer:
One real solution is – 1; then x3 + x2 + 9x + 9 = (x + 1)(x2 + 9) = (x + 1)(x – 3i)(x + 3i).
The solutions are – 1, 3i, – 3i.
d. x3 + 4x = 0
Answer:
One real solution is 0; then (x3 + 4x) = x(x2 + 4) = x(x + 2i)(x – 2i).
The solutions are 0, 2i, – 2i.
e. x3 + x2 + 2x + 2 = 0
Answer:
One real solution is x = – 1; then x3 + x2 + 2x + 2 = (x + 1)(x2 + 2) = (x + 1)(x – i\(\sqrt{2}\))(x + i\(\sqrt{2}\)).
The solutions are – 1, i\(\sqrt{2}\), – i\(\sqrt{2}\).
Question 3.
Find the solutions of the following equations.
a. 4x4 – x2 – 18 = 0
Answer:
Set u = x2. Then
4x4 – x2 – 18 = 4u2 – u – 18
= (4u – 9)(u + 2)
= (4x2 – 9)(x2 + 2)
= (2x – 3)(2x + 3)(x + i\(\sqrt{2}\))(x – i\(\sqrt{2}\))
The solutions are i\(\sqrt{2}\), – i\(\sqrt{2}\), – \(\frac{3}{2}\), \(\frac{3}{2}\).
b. x3 – 8 = 0
Answer:
(x3 – 8) = (x – 2)(x2 + 2x + 4)
= (x – 2)(x – ( – 1 – i\(\sqrt{3}\)))(x – ( – 1 + i\(\sqrt{3}\)))
The solutions are 2, – 1 + i\(\sqrt{3}\), – 1 – i\(\sqrt{3}\).
c. 8x3 – 27 = 0
Answer:
(8x3 – 27) = (2x – 3)(4x2 + 6x + 9)
= (2x – 3)(2x – (\(\frac{ – 3 – 3 i \sqrt{3}}{2}\)))(2x – (\(\frac{ – 3 + 3 i \sqrt{3}}{2}\)))
The solutions are \(\frac{3}{2}\), – \(\frac{3}{4}\) + \(\frac{3 i \sqrt{3}}{4}\), – 3/4 – \(\frac{3 i \sqrt{3}}{4}\).
d. x4 – 1 = 0
Answer:
(x4 – 1) = (x2 – 1)(x2 + 1)
= (x – 1)(x + 1)(x + i)(x – i)
The solutions are 1, – 1, i, – i.
e. 81x4 – 64 = 0
Answer:
(81x4 – 64) = (9x2 – 8)(9x2 + 8)
= (3x – 2\(\sqrt{2}\))(3x + 2\(\sqrt{2}\))(3x + 2i\(\sqrt{2}\))(3x – 2i\(\sqrt{2}\) )
The solutions are \(\frac{2 \sqrt{2}}{3}\) i, – \(\frac{2 \sqrt{2}}{3}\) i, \(\frac{2 \sqrt{2}}{3}\), – \(\frac{2 \sqrt{2}}{3}\).
f. 20x4 + 121x2 – 25 = 0
Answer:
(20x4 + 121x2 – 25) = (4x2 + 25)(5x2 – 1)
= (2x + 5i)(2x – 5i)(\(\sqrt{5}\)x – 1)(\(\sqrt{5}\)x + 1)
The solutions are \(\frac{5}{2}\)i, – \(\frac{5}{2}\) i, \(\frac{\sqrt{5}}{5}\), – \(\frac{\sqrt{5}}{5}\).
g. 64x3 + 27 = 0
amns:
(64x3 + 27) = (4x + 3)(16x\(\sqrt{2}\) – 12x + 9)
= (4x + 3)(8x – 3(1 – i\(\sqrt{3}\)))(8x – 3(1 + i\(\sqrt{3}\)))
The solutions are \(\frac{3}{8}\) + \(\frac{3 i \sqrt{3}}{8}\), – \(\frac{3}{4}\), \(\frac{3}{8}\) – \(\frac{3 i \sqrt{3}}{8}\).
h. x3 + 125 = 0
Answer:
(x3 + 125) = (x + 5)(x\(\sqrt{2}\) – 5x + 25)
= (x + 5)(x – \(\frac{5(1 – i \sqrt{3})}{2}\))(x – \(\frac{5(1 + i \sqrt{3})}{2}\))
The solutions are – 5, \(\frac{5}{2}\) + \(\frac{5 i \sqrt{3}}{2}\), \(\frac{5}{2}\) – \(\frac{5 i \sqrt{3}}{2}\).
Eureka Math Precalculus Module 3 Lesson 1 Exit Ticket Answer Key
Question 1.
Find the solutions of the equation x4 – x2 – 12. Show your work.
Answer:
x4 – x2 – 12 = (x2 + 3)(x2 – 4) = (x – i\(\sqrt{3}\))(x + i\(\sqrt{3}\))(x – 2)(x + 2) = 0
The solutions of the equation are i\(\sqrt{3}\), – i\(\sqrt{3}\), 2, – 2.
Question 2.
The number 1 is a zero of the polynomial p(x) = x3 – 3x2 + 7x – 5.
a. Write p(x) as a product of linear factors.
Answer:
(x – 1)(x2 – 2x + 5)
(x – 1)(x – (1 + 2i))(x – (1 – 2i))
b. What are the solutions to the equation x3 – 3x2 + 7x – 5 = 0?
Answer:
The solutions are 1, 1 + 2i, and 1 – 2i.