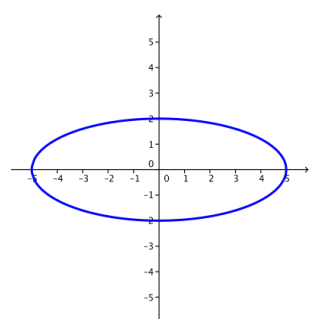
Engage NY Eureka Math Precalculus Module 3 Lesson 6 Answer Key
Eureka Math Precalculus Module 3 Lesson 6 Example Answer Key
Example 1.
Consider again the set of complex numbers represented by z = 3(cos(θ) + i sin(θ) ) for 0° ≤ θ < 360°.
Answer:
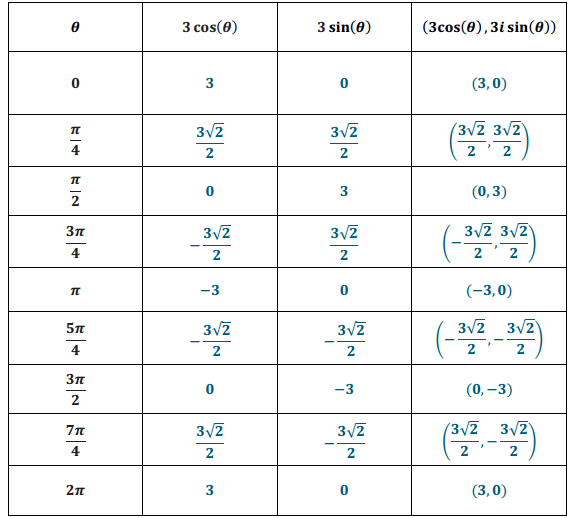
a. Use an ordered pair to write a representation for the points defined by z as they would be represented in the coordinate plane.
Answer:
(3 cos(θ),3 sin(θ) )
b. Write an equation that is true for all the points represented by the ordered pair you wrote in part (a).
Answer:
Since x = 3 cos(θ) and y = 3 sin(θ):
x2 + y2 = (3 cos(θ) )2 + (3 sin(θ) )2
x2 + y2 = 9(cos(θ) )2 + 9(sin(θ) )2
x2 + y2 = 9((cos(θ) )2 + (sin(θ) )2 )
We know that (sin(θ) )2 + (cos(θ) )2 = 1, so x2 + y2 = 9.
c. What does the graph of this equation look like in the coordinate plane?
Answer:
The graph is a circle centered at the origin with radius 3 units.
Example 2.
The equation of an ellipse is given by \(\frac{x^{2}}{16} + \frac{y^{2}}{4}\) = 1.
a. Sketch the graph of the ellipse.
Answer:
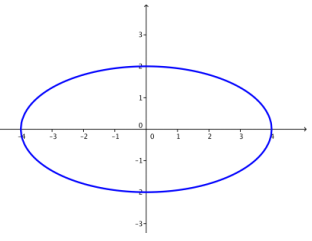
b. Rewrite the equation in complex form.
Answer:
\(\frac{x^{2}}{16} + \frac{y^{2}}{4}\) = 1
Since \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1, we have a = 4 and b = 2.
The complex form of the ellipse is z = a cos(θ) + bi sin(θ) = 4 cos(θ) + 2i sin(θ).
Example 3.
A set of points in the complex plane can be represented in the complex plane as z = 2 + i + 7 cos(θ) + i sin(θ) as θ varies.
a. Find an algebraic equation for the points described.
Answer:
z = 2 + i + 7 cos(θ) + i sin(θ) = (2 + 7 cos(θ) ) + i(1 + sin(θ) )
Since z = x + iy, then x = 2 + 7 cos(θ) and y = 1 + sin(θ).
So cos(θ) = \(\frac{x – 2}{7}\) and sin(θ) = (y – 1).
Since cos2(θ) + sin2(θ) = 1, we have (\(\frac{x – 2}{7}\))2 + (y – 1)2 = 1, which is equivalent to
\(\frac{(x – 2)^{2}}{49}\) + (y – 1)2 = 1.
b. Sketch the graph of the ellipse.
Answer:
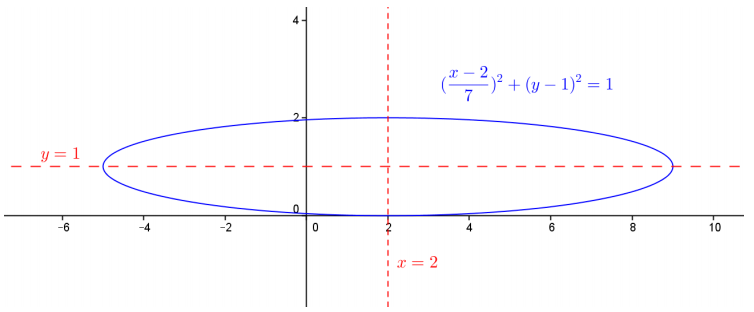
Eureka Math Precalculus Module 3 Lesson 6 Exercise Answer Key
Opening Exercise
a. Consider the complex number z = a + bi.
i. Write z in polar form. What do the variables represent?
Answer:
z = r(cos(θ) + i sin(θ) ), where r is the modulus of the complex number and θ is the argument.
ii. If r = 3 and θ = 90°, where would z be plotted in the complex plane?
Answer:
The point z is located 3 units above the origin on the imaginary axis.
iii. Use the conditions in part (ii) to write z in rectangular form. Explain how this representation corresponds to the location of z that you found in part (ii).
Answer:
z = a + bi, where a = r cos(θ) and b = r sin(θ)
a = 3 cos(90°) = 0; b = 3 sin(90°) = 3
Then z = 3i, which is located three units above the origin on the imaginary axis.
b. Recall the set of points defined by z = 3(cos(θ) + i sin(θ) ) for 0° ≤ θ < 360°, where θ is measured in degrees.
i. What does z represent graphically? Why?
Answer:
It is the set of points that are 3 units from the origin in the complex plane. This is because the modulus is 3, which indicates that for any given value of θ, z is located a distance of 3 units from the origin.
ii. What does z represent geometrically?
Answer:
A circle with radius 3 units centered at the origin
c. Consider the set of points defined by z = 5 cos(θ) + 3i sin(θ).
i. Plot z for θ = 0°, 90°, 180°, 270°, 360°. Based on your plot, form a conjecture about the graph of the set of complex numbers.
Answer:
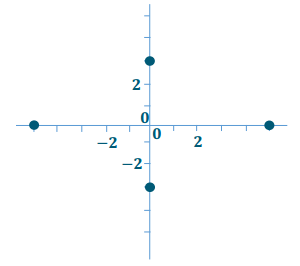
For θ = 0°, z = 5 cos(0°) + 3i sin(0°) = 5 + 0i ↔ (5,0).
For θ = 90°, z = 5 cos(90°) + 3i sin(90°) = 3i ↔ (0,3i).
For θ = 180°, z = 5 cos(180°) + 3i sin(180°) = – 5 + 0i ↔ ( – 5,0).
For θ = 270°, z = 5 cos(270°) + 3i sin(270°) = – 3i ↔ (0, – 3i).
This set of points seems to form an oval shape centered at the origin.
ii. Compare this graph to the graph of z = 3(cos(θ) + i sin(θ) ). Form a conjecture about what accounts for the differences between the graphs.
Answer:
The coefficients of cos(θ) and i sin(θ) are equal for z = 3(cos(θ) + i sin(θ) ), which results in a circle, which has a constant radius, while the coefficients are different for z = 5 cos(θ) + 3i sin(θ), which seems to stretch the circle.
Exercises 1–2
Exercise 1.
Recall the set of points defined by z = 5 cos(θ) + 3i sin(θ).
a. Use an ordered pair to write a representation for the points defined by z as they would be represented in the coordinate plane.
Answer:
(5 cos(θ), 3 sin(θ) )
b. Write an equation in the coordinate plane that is true for all the points represented by the ordered pair you wrote in part (a).
Answer:
We have x = 5 cos(θ) and y = 3 sin(θ), so x2 = 25(cos2(θ) ) and y2 = 9(sin2(θ) ). We know
(cos2(θ) + sin2(θ) ) = 1.
Since x2 = 25(cos2(θ) ), then cos2 (θ) = \(\frac{x^{2}}{25}\). Since y2 = 9(sin2(θ) ), then sin2 (θ) = \(\frac{x^{2}}{9}\). By substitution, \(\frac{x^{2}}{25} + \frac{y^{2}}{9}\) = 1.
Exercise 2.
Find an algebraic equation for all the points in the coordinate plane traced by the complex numbers z = \(\sqrt{2}\) cos(θ) + i sin(θ).
Answer:
All the complex numbers represented by z can be written using the ordered pair (\(\sqrt{2}\) cos(θ),sin(θ) ) in the coordinate plane.
We have x = \(\sqrt{2}\) cos(θ) and y = sin(θ), so x2 = 2 cos2(θ) and y2 = sin2 (θ). We know cos2 (θ) + sin2 (θ) = 1.
Since x2 = 2 cos2(θ), then cos2 (θ) = \(\frac{x^{2}}{2}\). Then, by substitution, \(\frac{x^{2}}{2}\) + y2 = 1.
Exercise 3.
The equation of an ellipse is given by \(\frac{x^{2}}{9} + \frac{y^{2}}{26}\) = 1.
a. Sketch the graph of the ellipse.
Answer:
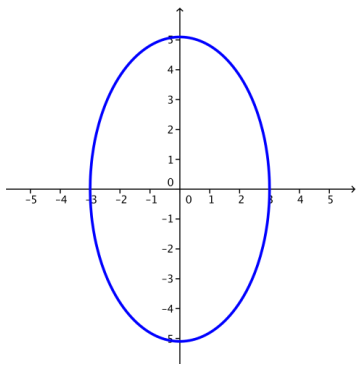
b. Rewrite the equation of the ellipse in complex form.
Answer:
\(\frac{x^{2}}{9} + \frac{y^{2}}{26}\) = 1
|a| = 3
|b| = \(\sqrt{26}\)
The complex form of the ellipse is z = a cos(θ) + bi sin(θ) = 3 cos(θ) + \(\sqrt{26}\)i sin(θ).
Eureka Math Precalculus Module 3 Lesson 6 Problem Set Answer Key
Question 1.
Write the real form of each complex equation.
a. z = 4 cos(θ) + 9i sin(θ)
Answer:
\(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{81}\) = 1
b. z = 6 cos(θ) + i sin(θ)
Answer:
\(\frac{x^{2}}{36}\) + y2 = 1
c. z = \(\sqrt{5}\) cos(θ) + \(\sqrt{10}\)i sin(θ)
Answer:
\(\frac{x^{2}}{5}\) + \(\frac{y^{2}}{10}\) = 1
d. z = 5 – 2i + 4 cos(θ) + 7i sin(θ)
Answer:
\(\frac{(x – 5)^{2}}{16} + \frac{(y + 2)^{2}}{49}\) = 1
Question 2.
Sketch the graphs of each equation.
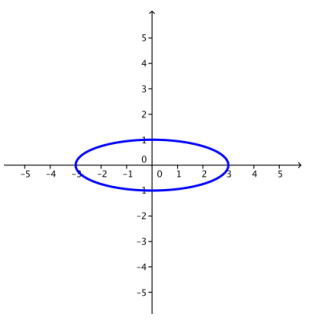
a. z = 3 cos(θ) + i sin(θ)
Answer:
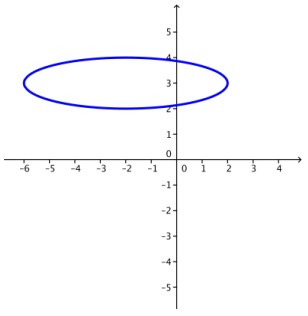
b. z = – 2 + 3i + 4 cos(θ) + i sin(θ)
Answer:
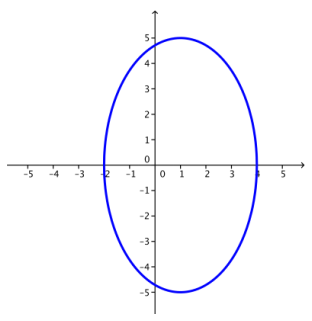
c. \(\frac{(x – 1)^{2}}{9} + \frac{y^{2}}{25}\) = 1
Answer:
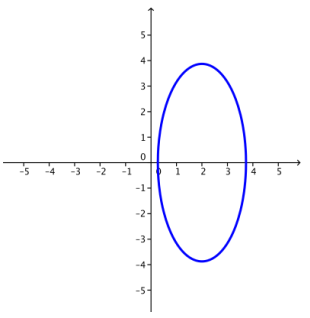
d. \(\frac{(x – 2)^{2}}{3} + \frac{y^{2}}{15}\) = 1
Answer:
Question 3.
Write the complex form of each equation.
a. \(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{36}\) = 1
Answer:
z = 4 cos(θ) + 6i sin(θ)
b. \(\frac{x^{2}}{400}\) + \(\frac{y^{2}}{169}\) = 1
Answer:
z = 20 cos(θ) + 13i sin(θ)
c. \(\frac{x^{2}}{19}\) + \(\frac{y^{2}}{2}\) = 1
Answer:
z = \(\sqrt{19}\)cos(θ) + \(\sqrt{2}\)i sin(θ)
d. \(\frac{(x – 3)^{2}}{100}\) + \(\frac{(y + 5)^{2}}{16}\) = 1
Answer:
z = 3 – 5i + 10 cos(θ) + 4i sin(θ)
Question 4.
Carrie converted the equation z = 7 cos(θ) + 4i sin(θ) to the real form \(\frac{x^{2}}{7}\) + \(\frac{y^{2}}{4}\) = 1. Her partner Ginger said that the ellipse must pass through the point (7 cos(0),4 sin(0) ) = (7,0) and this point does not satisfy Carrie’s equation, so the equation must be wrong. Who made the mistake, and what was the error? Explain how you know.
Answer:
Ginger is correct. Carrie set a = 7 and b = 4, which is correct, but then she made an error in converting to the real form of the equation by dividing by a and b instead of a2 and b2.
Question 5.
Cody says that the center of the ellipse with complex equation z = 4 – 5i + 2 cos(θ) + 3i sin(θ) is (4, – 5), while his partner, Jarrett, says that the center of this ellipse is ( – 4,5). Which student is correct? Explain how you know.
Answer:
Cody is correct. This ellipse is the translation of the ellipse with equation z = 2 cos(θ) + 3i sin(θ) by the vector 〈4, – 5〉, which moves the center of the ellipse from the origin to the point (4, – 5).
Extension:
Question 6.
Any equation of the form ax2 + bx + cy2 + dy + e = 0 with a>0 and c>0 might represent an ellipse. The equation 4x2 + 8x + 3y2 + 12y + 4 = 0 is such an equation of an ellipse.
a. Rewrite the equation \(\frac{(x – h)^{2}}{a^{2}}\) + \(\frac{(y – k)^{2}}{b^{2}}\) = 1 in standard form to locate the center of the ellipse (h,k).
Answer:
4(x2 + 2x) + 3(y2 + 4y) + 4 = 0
4(x2 + 2x + 1) + 3(y2 + 4y + 4) = – 4 + 4(1) + 3(4)
4(x + 1)2 + 3(y + 2)2 = 12
\(\frac{4(x + 1)^{2}}{12}\) + \(\frac{3(y + 2)^{2}}{12}\) = 1
\(\frac{(x + 1)^{2}}{3}\) + \(\frac{(y + 2)^{2}}{4}\) = 1
The center of the ellipse is the point ( – 1, – 2).
b. Describe the graph of the ellipse, and then sketch the graph.
Answer:
The graph of the ellipse is centered at ( – 1, – 2). It is elongated vertically with a semi – major axis of length 2 units and a semi – minor axis of length \(\sqrt{3}\) units.
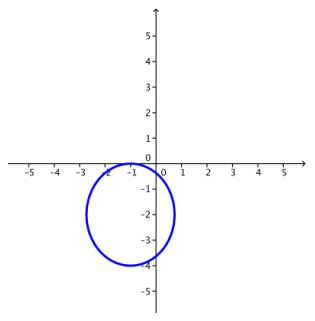
c. Write the complex form of the equation for this ellipse.
Answer:
\(\frac{(x + 1)^{2}}{3}\) + \(\frac{(y + 2)^{2}}{4}\) = 1
cos2(θ) + sin2(θ) = 1, so cos2(θ) = \(\frac{(x + 1)^{2}}{3}\) and sin2(θ) = \(\frac{(y + 2)^{2}}{4}\)
3 cos2(θ) = (x + 1)2, so x = \(\sqrt{3}\) cos(θ) – 1
4 sin2(θ) = (y + 2)2, so y = 2 sin(θ) – 2
z = x + iy
= \(\sqrt{3}\) cos(θ) – 1 + i(2 sin(θ) – 2)
= – 1 – 2i + \(\sqrt{3}\) cos(θ) + 2i sin(θ)
Eureka Math Precalculus Module 3 Lesson 6 Exit Ticket Answer Key
Question 1.
Write the real form of the complex equation z = cos(θ) + 3i sin(θ). Sketch the graph of the equation.
Answer:
x2 + \(\frac{y^{2}}{9}\) = 1
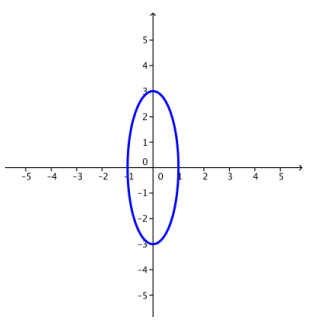
Question 2.
Write the complex form of the equation \(\frac{x^{2}}{25} + \frac{y^{2}}{4}\) = 1. Sketch the graph of the equation.
Answer:
z = 5 cos(θ) + 2i sin(θ)