Engage NY Eureka Math Precalculus Module 1 Lesson 13 Answer Key
Eureka Math Precalculus Module 1 Lesson 13 Example Answer Key
Example 1.
The Polar Form of a Complex Number
Derive a formula for a complex number in terms of its modulus r and argument θ.
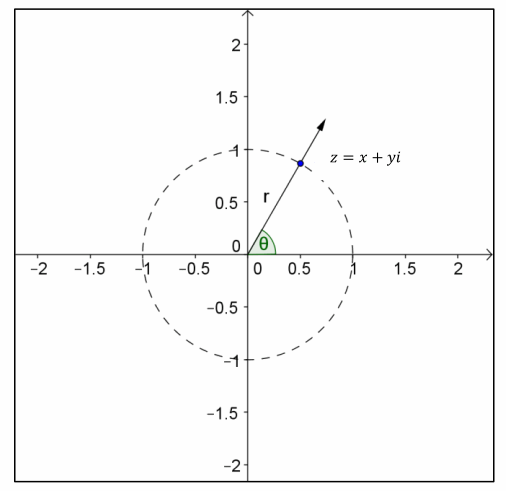
Suppose that z has coordinates (x,y) that lie on the unit circle as shown.
a. What is the value of r, and what are the coordinates of the point (x,y) in terms of θ? Explain how you know.
Answer:
The value of r is 1. The coordinates of the point are (cos(θ), sin(θ)). The definition of the sine and cosine function says that a point on the unit circle where a rotated ray intersects the unit circle has these coordinates.
b. If r=2, what would be the coordinates of the point (x,y)? Explain how you know.
Answer;
The coordinates would be (2 cos(θ), 2sin(θ) ) because the point lies along the same ray but are just dilated by a scale factor of two along the ray from the origin compared to when r=1.
c. If r=20, what would be the coordinates of the point (x,y)? Explain how you know.
Answer:
The coordinates would be (20 cos(θ),20 sin(θ) ) because a circle of radius 20 units would be similar to a circle with radius 1 but dilated by a factor of 20.
d. Use the definitions of sine and cosine to write coordinates of the point (x,y) in terms of cosine and sine for any r≥0 and real number θ.
Answer:
x=r cos(θ) and y=r sin(θ)
e. Use your answer to part (d) to express z=x+yi in terms of r and θ.
Answer:
z=x+yi=r cos(θ)+ir sin(θ)=r(cos(θ)+i sin(θ) )
Monitor students as they work in small groups to derive the polar form of a complex number from the rectangular form. After a few minutes, ask for a few volunteers to share their ideas, and then make sure to have students record the derivation shown below in their notes and revise their work to be accurate and precise.
Annotate the diagram above showing that the x- and y-values correspond to the points on a circle of radius r that is a dilation of the unit circle. Thus, the point (x,y) can be represented as (r cos(θ),r sin(θ) ).
→ The diagram shown above makes us recall the definitions of sine and cosine. We see from the following diagram:
x=r cos(θ) and y=r sin(θ).
→ Which means that every complex number can be written in the form:
z=x+iy=r cos(θ)+ir sin(θ)=r(cos(θ)+i sin(θ)).
Review the definition shown below, and then have students work in small groups to answer Exercises 3–6.
POLAR FORM OF A COMPLEX NUMBER: The polar form of a complex number z is r(cos(θ)+ i sin(θ) ), where r=|z| and
θ=arg(z).
RECTANGULAR FORM OF A COMPLEX NUMBER: The rectangular form of a complex number z is a+bi, where z corresponds to the point (a,b) in the complex plane, and i is the imaginary unit. The number a is called the real part of a+bi, and the number b is called the imaginary part of a+bi.
Use the graphic organizer below to help students make sense of this definition. A blank version is included in the student materials. The graphic organizer has space for up to three examples of complex numbers that can either be completed as a class or assigned to students. Have students work with a partner to provide the polar and rectangular forms of both numbers. Have partners take turns explaining why the polar and rectangular forms of the examples represent the same number.

Answer:

Explain to students that this form of a complex number is particularly useful when considering geometric representations of complex numbers. This form clearly shows that every complex number z can be described as a rotation of θ° and a dilation by a factor of r of the real number 1.
Example 2.
Writing a Complex Number in Polar Form
a. Convert 3+4i to polar form.
Answer:
5(cos(53.1°)+i sin(53.1°) )
b. Convert 3-4i to polar form.
Answer:
5(cos(306.9°)+i sin(306.9°) )
→ What is the modulus of 3+4i?
→ The modulus is 5.
Draw a diagram like the one shown below, and use trigonometry ratios to help you determine the argument. Plot the point (3,4), and draw a line segment perpendicular to the x-axis from the point to the x-axis. Draw the ray from the origin through the point (3,4) and the ray from the origin through the real number 1. Label the acute angle between these rays θ.
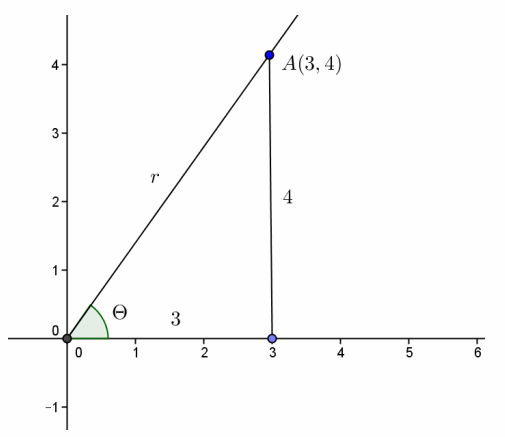
→ The line segment from (0,0) to (3,0), the line segment we just drew, and the segment from the origin to the point form a right triangle. What is the tangent ratio of the acute angle whose vertex is at the origin?
→ The tangent is tan(θ)=\(\frac{4}{3}\).
→ Use a calculator to estimate the measure of this angle. What is the argument of 3+4i?
→ We can use θ=arctan(\(\frac{4}{3}\)). Rounded to the nearest hundredth, θ=53.1°.
→ Write 3+4i in polar form.
→ The polar form is 5(cos(53.1°)+i sin(53.1°) ) with the angle rounded to the nearest tenth.
Part (b) of this example shows how the process above needs to be tweaked when the complex number is not located in the first quadrant.
The modulus is 5. When we plot the point (3,-4) and draw a line segment perpendicular to the x-axis, we can see that the acute angle at the origin in this triangle will still have a measure equal to arctan(\(\frac{4}{3}\))=53.1°.
Model how to draw this diagram so students see how to use the arctangent function to find the measure of the acute angle at the origin in the triangle they constructed.
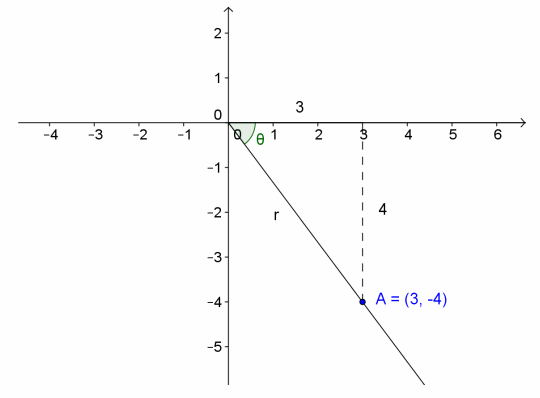
→ Use your knowledge of angles to determine the argument of 3-4i. Explain your reasoning.
→ An argument of 3-4i would be 360°-53.1°=306.9°. The positive rotation of ray from the origin containing the real number 1 that maps to a ray passing through this point would be 53° less than a full rotation of 360°.
→ What is the polar form of 3-4i?
→ The polar form is 5(cos(306.9°)+i sin(306.9°)).
→ Why do the polar and rectangular forms of a complex number represent the same number?
→ 3-4i can be thought of as the point (3,-4) in the complex plane. The point can be located by extending the ray from the origin rotated 306.9°. The point is a distance of 5 units (the modulus) from the origin along that ray.
Eureka Math Precalculus Module 1 Lesson 13 Exercise Answer Key
Opening Exercise
For each complex number shown below, answer the following questions. Record your answers in the table.
a. What are the coordinates (a,b) that correspond to this complex number?
b. What is the modulus of the complex number?
c. Suppose a ray from the origin that contains the real number 1 is rotated θ° so it passes through the point (a,b). What is a value of θ?
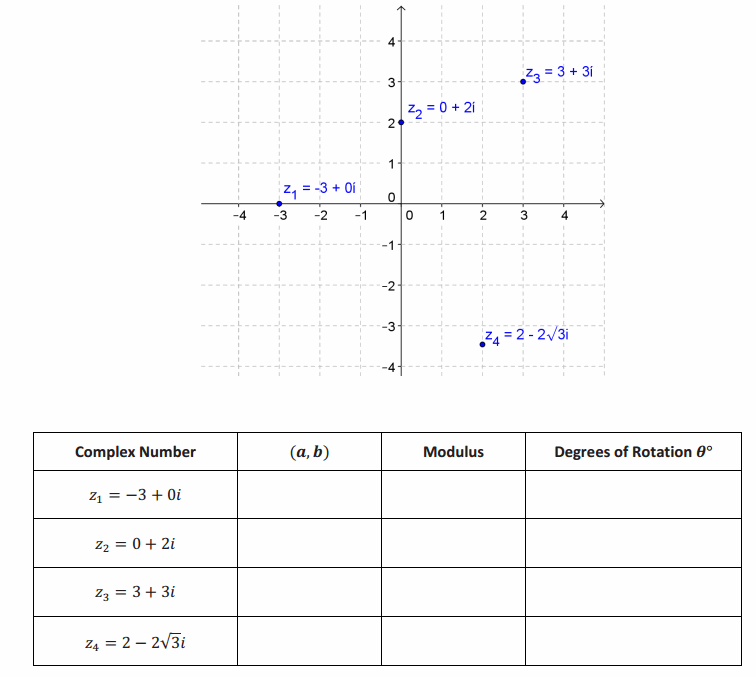
Answer:
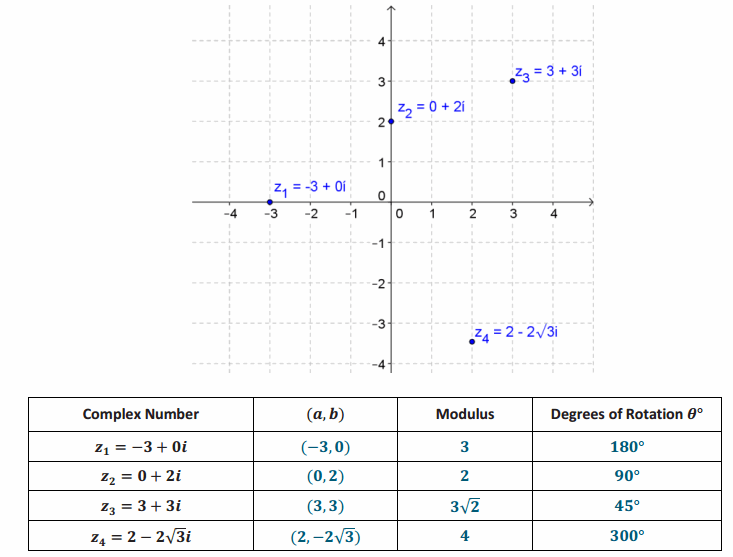
As students present their solutions, ask if anyone has a different answer for the number of degrees of the rotation, and lead a discussion so students understand that the degrees of rotation have more than one possible answer and, in fact, there are infinitely many possible answers.
→ Another student said that a clockwise rotation of 270° would work for z2. Do you agree or disagree? Explain.
→ I agree. This rotation also takes the initial ray from the origin to a ray containing the point 0+2i. If a complete rotation is 360°, then 270° clockwise would be the same as 90° counterclockwise.
At this point, remind students that positive rotations are counterclockwise and that rotation in the opposite direction is denoted using negative numbers.
Exercises 1–2
Exercise 1.
Can you find at least two additional rotations that would map a ray from the origin through the real number 1 to a ray from the origin passing through the point (3,3)?
Answer:
This is the number z3=3+3i from the Opening Exercise. Additional rotations could be 45°+360°=405° or 45°-360°=-315°.
Exercise 2.
How are the rotations you found in Exercise 1 related?
Answer:
All rotations that take the initial ray to the ray described above must be of the form 45°+360°n for integer values of n.
After reviewing possible solutions to the questions above, pose this next question. It may be written on the board. Give students a few minutes to think about their responses individually, and then have them discuss them with their partners or group members before sharing responses as a whole class.
→ Do you think it is possible to describe a complex number in terms of its modulus and the degrees of rotation of a ray from the origin containing the real number 1? Justify your reasoning.
→ Student responses will vary. In general, the response should be yes, but careful students should note the difficulty of uniquely defining degrees of rotation. The modulus will be a distance from the origin, and if we want to be precise, we may need to limit the possible degrees of rotation to a subset of the real numbers such as 0°≤θ<360°.
Discussion
Exercises 2 and 3 show that the rotation that maps a ray from the origin containing the real number 1 to a ray containing a given complex number is not unique. If you know one rotation, you can write an expression that represents all the rotations of a given complex number z. However, if we limit the rotations to an interval that comprises one full rotation of the initial ray, then we can still describe every complex number in terms of its modulus and a rotation.
Introduce the modulus and argument of a complex number.
Every complex number z=x+yi appears as a point on the complex plane with coordinates (x,y) as a point in the coordinate plane.
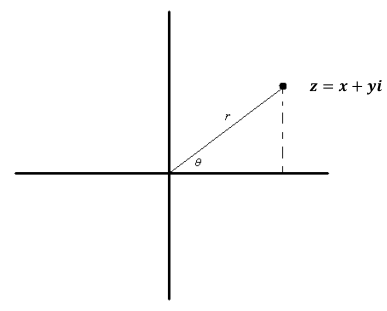
In the diagram above, notice that each complex number z has a distance r from the origin to the point (x,y) and a rotation of θ° that maps the ray from the origin along the positive real axis to the ray passing through the point (x,y).
ARGUMENT OF THE COMPLEX NUMBER z: The argument of the complex number z is the radian (or degree) measure of the counterclockwise rotation of the complex plane about the origin that maps the initial ray (i.e., the ray corresponding to the positive real axis) to the ray from the origin through the complex number z in the complex plane. The argument of z is denoted arg(z).
MODULUS OF A COMPLEX NUMBER Z: The modulus of a complex number z, denoted |z|, is the distance from the origin to the point corresponding to z in the complex plane. If z=a+bi, then |z|=\(\sqrt{a^{2}+b^{2}}\).
→ Is “modulus” indeed the right word? Does r=|z| as we defined it in previous lessons?
→ Yes, since r is the distance from the origin to the point (x,y), which is \(\sqrt{x^{2}+y^{2}}\), which is also how we define the modulus of a complex number.
→ Why are we limiting the argument to a subset of the real numbers?
→ We only need these angles to sweep through all possible points in the coordinate plane. If we allowed the argument to be any real number, there would be many possible arguments for any given complex number.
Exercises 3–6
Exercise 3.
Write each complex number from the Opening Exercise in polar form.

Answer:

Exercise 4.
Use a graph to help you answer these questions.
a. What is the modulus of the complex number 2-2i?
Answer:
If you graph the point (2,-2), then the distance between the origin and the point is given by the distance formula, so the modulus would be \(\sqrt{(2)^{2}+(-2)^{2}}\)=2\(\sqrt{2}\).
b. What is the argument of the number 2-2i?
Answer:
If you graph the point (2,-2), then the rotation that will take the ray from the origin through the real number 1 to a ray containing that point will be 315° because the point lies on a line from the origin in Quadrant IV that is exactly in between the two axes. The argument would be 315°. We choose that rotation because we defined the argument to be a number between 0 and 360.
c. Write the complex number in polar form.
Answer:
2\(\sqrt{2}\)(cos(315°)+i sin(315°) )
d. Arguments can be measured in radians. Express your answer to part (c) using radians.
Answer:
In radians, 315° is \(\frac{7 \pi}{4}\); the number would be
2\(\sqrt{2}\)(cos(\(\frac{7 \pi}{4}\))+i sin(\(\frac{7 \pi}{4}\)) ).
e. Explain why the polar and rectangular forms of a complex number represent the same number.
Answer:
2-2i is thought of as a point with coordinates (2,-2) in the complex plane. The point can also be located by thinking of the ray extending from the origin rotated 315°. The distance from the origin to the point along that ray is the modulus, which is 2\(\sqrt{2}\)units.
Debrief Exercises 3 and 4 by having one or two students volunteer their solutions. On Exercise 4, some students may use right-triangle trigonometry while others take a more geometric approach and reason out the value of the argument from the graph and their knowledge of special right triangles. Pause and review radian measure if students are struggling to answer Exercise 4, part (d). When reviewing these first two exercises, be sure to emphasize why the work from Example 1 validates that the polar and rectangular forms of a complex number represent the same number.
Next, give students a few minutes to work individually on using this new form of a complex number. They need to approximate the location of a few of these rotations unless provided with a protractor. If the class is struggling to evaluate trigonometric functions of special angles, students may use a calculator, a copy of the unit circle, or their knowledge of special triangles to determine the values of a and b. Students need a calculator to answer Exercise 6,
part (c).
Exercise 5.
State the modulus and argument of each complex number, and then graph it using the modulus and argument.
a. 4(cos(120°)+i sin(120°))
Answer:
r=4, θ=120°
b. 5(cos(\(\frac{π}{4}\))+i sin(\(\frac{π}{4}\)) )
Answer:
r=5, θ=\(\frac{π}{4}\)
c. 3(cos(190°)+i sin(190°))
Answer:
r=3, θ=190°
Exercise 6.
Evaluate the sine and cosine functions for the given values of θ, and then express each complex number in rectangular form, z=a+bi. Explain why the polar and rectangular forms represent the same number.
a. 4(cos(120°)+i sin(120°))
Answer;
4(-\(\frac{1}{2}\)+(\(\frac{\sqrt{3} i}{2}\))=-2+2\(\sqrt{3} i\)
The polar form of a complex number and the rectangular form represent the same number because they both give you the same coordinates of a point that represents the complex number. In this example, 4 units along a ray from the origin rotated 120° corresponds to the coordinate (-2,2\(\sqrt{3}\)).
b. 5(cos(\(\frac{π}{4}\))+i sin(\(\frac{π}{4}\)) )
Answer:
5(\(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{2} i}{2}\))=\(\frac{5 \sqrt{2}}{2}\)+\(\frac{5 \sqrt{2} i}{2}\)
The polar form and rectangular form represent the same number because the values of 5 cos(\(\frac{π}{4}\)) and 5 sin(\(\frac{π}{4}\)) are exactly \(\frac{5 \sqrt{2}}{2}\).
c. 3(cos(190° )+i sin(190°))
Answer:
Rounded to two decimal places, the rectangular form is -2.95-0.52i. This form of the number is close to, but not exactly, the same as the number expressed in polar form because the values of the trigonometric functions are rounded to the nearest hundredth.
Review the solutions to these exercises with the entire class to check for understanding before moving on to Example 2. Make sure students understand that in Exercise 6, they rewrote each complex number given in polar form as an equivalent complex number written in rectangular form. Emphasize that in part (c), the rectangular form is an approximation of the polar form.
Exercise 7.
Express each complex number in polar form. State the arguments in radians rounded to the nearest thousandth.
a. 2+5i
Answer:
arg(2+5i)=tan-1(\(\frac{5}{2}\))≈1.190
|2+5i|=\(\sqrt{4+25}\)=\(\sqrt{29}\)
2+5i≈\(\sqrt{29}\) (cos(1.190)+i sin(1.190) )
b. -6+i
Answer;
arg(z)=π-tan-1(\(\frac{1}{6}\))≈2.976
|-6+i|=\(\sqrt{37}\)
-6+i=\(\sqrt{37}\) (cos(2.976)+i sin(2.976))
Eureka Math Precalculus Module 1 Lesson 13 Exit Ticket Answer Key
Question 1.
State the modulus and argument of each complex number. Explain how you know.
a. 4+0i
Answer:
The modulus is 4, and the argument is 0°. The real number 4 is 4 units from the origin and lies in the same position as a ray from the origin containing the real number 1, so the rotation is 0°.
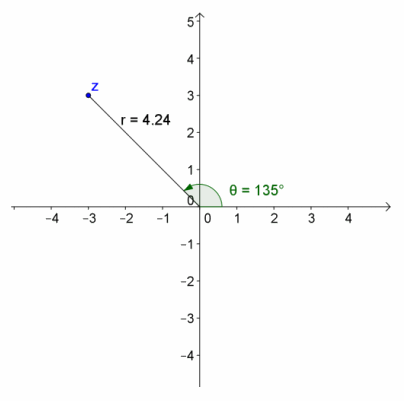
b. -2+2i
Answer:
The modulus is 2\(\sqrt{2}\), and the argument is 135°. The values of a and b correspond to sides of a 45°–45°–90° right triangle, so the modulus would be 2\(\sqrt{2}\), and the rotation is 45° less than 180°.
Question 2.
Write each number from Problem 1 in polar form.
Answer:
a. 4(cos(0°)+i sin(0°) )
b. 2\(\sqrt{2}\)(cos(135°)+i sin(135°) )
Question 3.
Explain why 5(cos(\(\frac{π}{6}\))+i sin(\(\frac{π}{6}\)) ) and \(\frac{5 \sqrt{3}}{2}\)+\(\frac{5}{2}\)i represent the same complex number.
Answer:
5(cos(\(\frac{π}{6}\))+isin(\(\frac{π}{6}\)) )
If you evaluate 5 cos(\(\frac{π}{6}\)) and 5 sin(\(\frac{π}{6}\)), you get \(\frac{5 \sqrt{3}}{2}\) and \(\frac{5}{2}\), respectively.
5(cos(\(\frac{π}{6}\))+i sin(\(\frac{π}{6}\)) )=\(\frac{5 \sqrt{3}}{2}\)+\(\frac{5}{2}\)i
\(\frac{5 \sqrt{3}}{2}\)+\(\frac{5}{2}\)i is thought of as a point with coordinates (\(\frac{5 \sqrt{3}}{2}\),\(\frac{5}{2}\)) in the complex plane. The point can also be located by thinking of the ray extending from the origin rotated \(\frac{π}{6}\) radians. The distance from the origin to the point along that ray is the modulus, which is 5 units.
Eureka Math Precalculus Module 1 Lesson 13 Problem Set Answer Key
Question 1.
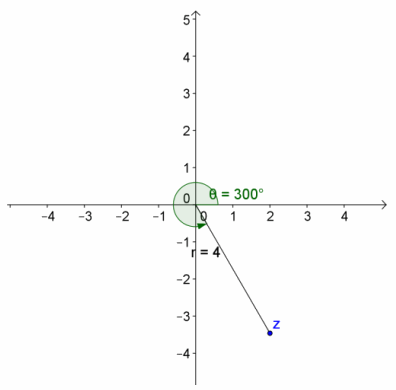
Explain why the complex numbers z1=1-\(\sqrt{3}\)i, z2=2-2\(\sqrt{3}\)i, and z3=5-5\(\sqrt{3}\)i can all have the same argument. Draw a diagram to support your answer.
Answer:
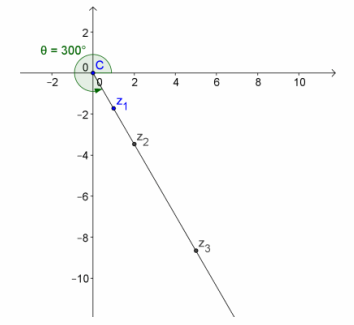
They all lie on the same ray from the origin that represents a 300° rotation.
Question 2.
What is the modulus of each of the complex numbers z1, z2, and z3 given in Problem 1 above?
Answer:
The moduli are 2, 4, and 10.
Question 3.
Write the complex numbers from Exercise 1 in polar form.
Answer:
z1=2(cos(300°)+i sin(300°) )
z2=4(cos(300°)+i sin(300°) )
z3=10(cos(300°)+i sin(300°) )
Question 4.
Explain why 1-\(\sqrt{3}\)i and 2(cos(300°)+i sin(300°) ) represent the same number.
Answer:
The point (1,-\(\sqrt{3}\)) lies on a ray from the origin that has been rotated 300° rotation from the initial ray. The distance of this point from the origin along this ray is 2 units (the modulus). Using the definitions of sine and cosine, any point along that ray will have coordinates (2 cos(300°),2 sin(300°) ).
Question 5.
Julien stated that a given modulus and a given argument uniquely determine a complex number. Confirm or refute Julien’s reasoning.
Answer:
Julien’s reasoning is correct. If you rotate a ray from the origin containing the real number 1 and then locate a point a fixed number of units along that ray from the origin, it will give you a unique point in the plane.
Question 6.
Identify the modulus and argument of the complex number in polar form, convert it to rectangular form, and sketch the complex number in the complex plane. 0°≤arg(z)≤360° or 0≤arg(z)≤2π (radians)
a. z=cos(30°)+i sin(30°)
Answer:
r=1, arg(z)=30°
z=( \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\)i
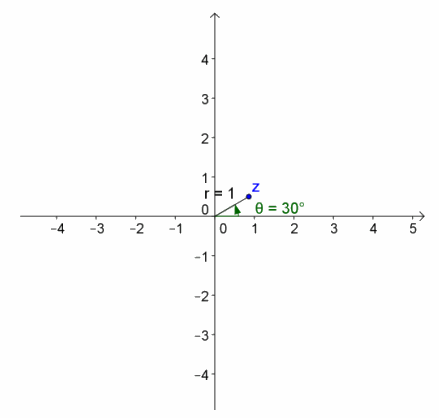
b. z=2(cos(\(\frac{π}{4}\))+i sin(\(\frac{π}{4}\)) )
Answer:
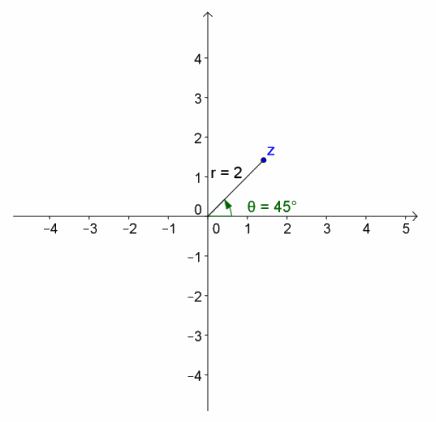
r=2, arg(z)=\(\frac{π}{4}\) radians
z=\(\sqrt{2}\)+\(\sqrt{2}\)i
c. z=4(cos(\(\frac{\pi}{3}\))+i sin(\(\frac{\pi}{3}\)) )
Answer:
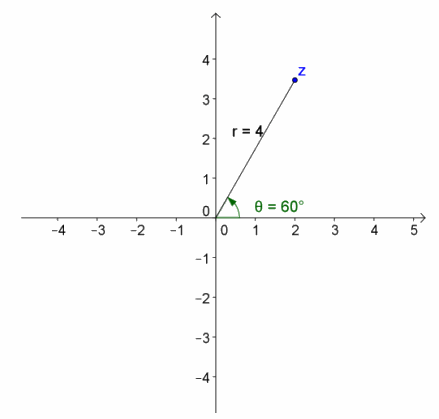
r=4, arg(z)=\(\frac{\pi}{3}\) ” radians”
z=2+2\(\sqrt{3}\)i
d. z=2\(\sqrt{3}\)(cos(\(\frac{5 \pi}{6}\))+i sin(\(\frac{5 \pi}{6}\))
Answer:
r=2\(\sqrt{3}\), arg(z)=\(\frac{5π}{6}\) radians
z=-3+\(\sqrt{3}\)i
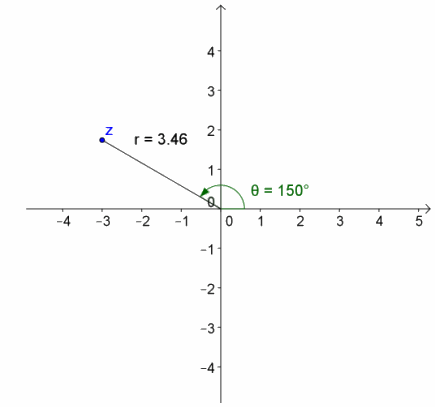
e. z=5(cos(5.637)+i sin(5.637) )
Answer:
r=5, arg(z)=5.637 radians
z=4-3i
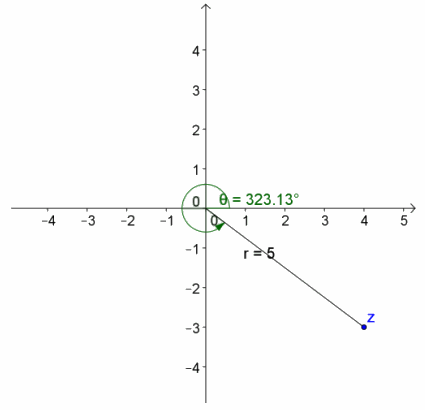
f. z=5(cos(2.498)+i sin(2.498) )
Answer:
r=5, arg(z)=2.498 radians
z=-4+3i
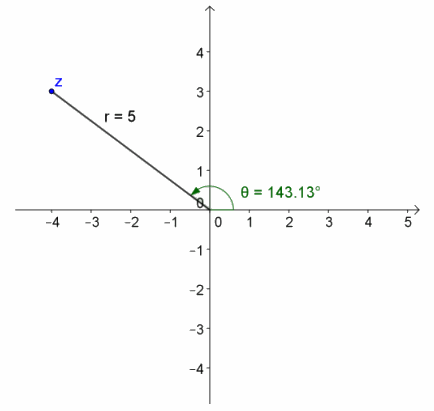
g. z=\(\sqrt{34}\)(cos(3.682)+i sin(3.682) )
Answer:
r=\(\sqrt{34}\), arg(z)=3.682
z=-5-3i
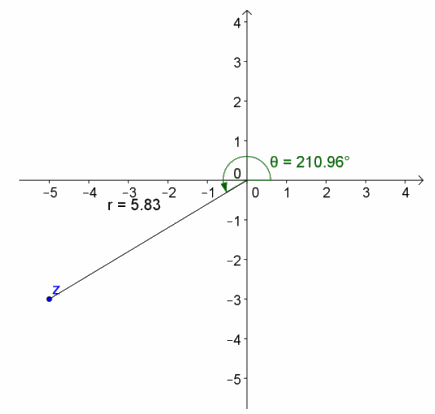
h. z=4\(\sqrt{3}\)(cos(\(\frac{5 \pi}{3}\)+i sin((\(\frac{5 \pi}{3}\)))
Answer:
r=4\(\sqrt{3}\), arg(z)=\(\frac{5 \pi}{3}\)
z=2\(\sqrt{3}\)-6i
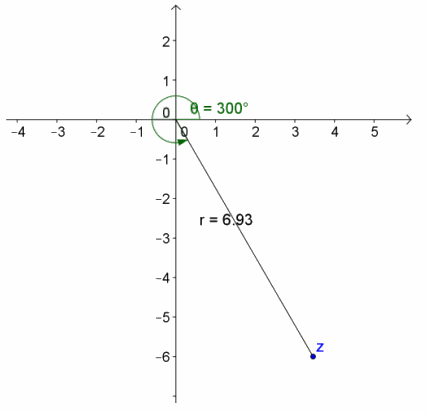
Question 7.
Convert the complex numbers in rectangular form to polar form. If the argument is a multiple of \(\frac{π}{6}\), \(\frac{π}{4}\), \(\frac{π}{3}\), or \(\frac{π}{2}\), express your answer exactly. If not, use arctan(\(\frac{b}{a}\)) to find arg(z) rounded to the nearest thousandth, 0≤arg(z)≤2π (radians).
a. z=\(\sqrt{3}\)+i
Answer:
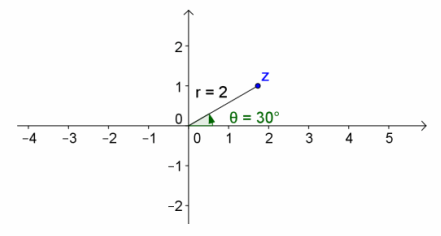
arg(z) is in Quadrant I.
arg(z)=arctan(\(\frac{b}{a}\))
=arctan(\(\frac{1}{\sqrt{3}}\))
=\(\frac{π}{6}\)
r=|z|
=\(\sqrt{(\sqrt{3})^{2}+(1)^{2}}\))
=2
z=2(cos(\(\frac{π}{6}\))+i sin(\(\frac{π}{6}\))
b. z=-3+3i
Answer:
arg(z) is in Quadrant II.
arg(z)=π-arctan(\(\frac{b}{a}\))
=π-arctan(\(\frac{3}{3}\))
=π-\(\frac{\pi}{4}\)
=\(\frac{3 \pi}{4}\)
r=|z|
=\(\sqrt{(-3)^{2}+(3)^{2}}\)
=3\(\sqrt{2}\)
z=3\(\sqrt{2}\)(cos(\(\frac{3 \pi}{4}\))+i sin(\(\frac{3 \pi}{4}\))
c. z=2-2\(\sqrt{3}\)i
Answer:
arg(z) is in Quadrant IV.
arg(z)=2π-arctan(\(\frac{b}{a}\))
=2π-arctan(\(\frac{2 \sqrt{3}}{2}\))
=2π-(\(\frac{\pi}{3}\))
=\(\frac{5 \pi}{3}\)radians
r=|z|
=\(\sqrt{(2)^{2}+(-2 \sqrt{3})^{2}}\)
=4
z=4(cos(\(\frac{5 \pi}{3}\))+i sin(\(\frac{5 \pi}{3}\)))
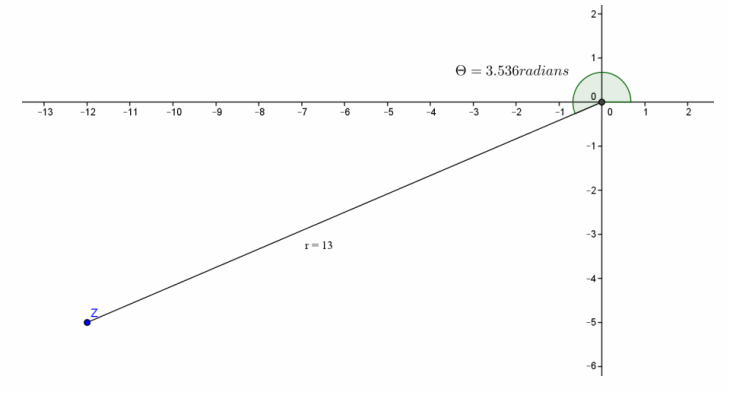
d. z=-12-5i
Answer:
arg(z) is in Quadrant III.
arg(z)=π+arctan(\(\frac{5}{12}\))
=π+arctan(\(\frac{1}{\sqrt{3}}\))
≈3.536 radians
r=|z|
=\(\sqrt{(-12)^{2}+(-5)^{2}}\)
=13
z=13(cos(3.536)+i sin(3.536) )
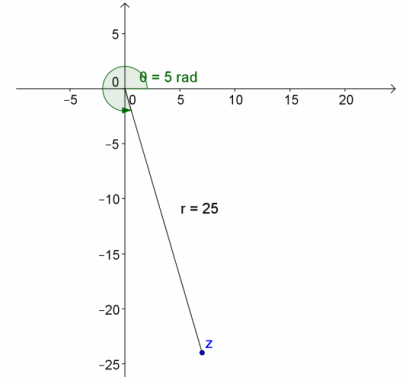
e. z=7-24i
Answer:
arg(z) is in Quadrant IV.
arg(z)=2π-arctan(\(\frac{b}{a}\))
=2π-arctan(\(\frac{24}{7}\))
≈4.996 radians
r=|z|
=\(\sqrt{(7)^{2}+(-24)^{2}}\)
=25
z=25(cos(4.996)+i sin(4.996) )
Question 8.
Show that the following complex numbers have the same argument.
a. z1=3+3\(\sqrt{3}\)i and z2=1+\(\sqrt{3}\)i
Answer:
arg(z1)=arctan(\(\frac{3 \sqrt{3}}{3}\))=\(\frac{\pi}{3}\) and arg(z2)=(\(\sqrt{3}\))=\(\frac{\pi}{3}\)
b. z1=1+i and z2=4+4i
Answer;
arg(z1)=arctan(\(\frac{1}{1}\))=\(\frac{π}{4}\) and arg(z2)=arctan(\(\frac{4}{4}\))=\(\frac{π}{4}\)
Question 9.
A square with side length of one unit is shown below. Identify a complex number in polar form that corresponds to each point on the square.
Answer:
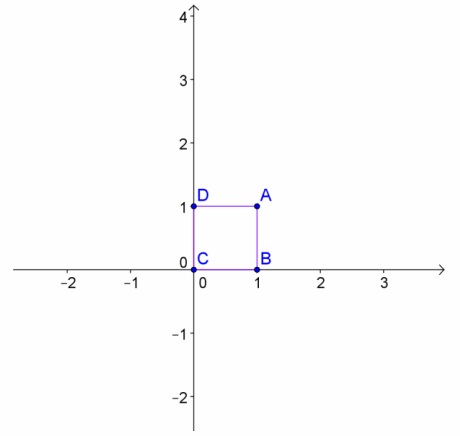
A=\(\sqrt{2}\)(cos(45°)+i sin(45°) )
B=1(cos(0°)+i sin(0°) )
C=0(cos(0°)+i sin(0°) )
D=1(cos(90°)+i sin(90°) )
Question 10.
Determine complex numbers in polar form whose coordinates are the vertices of the square shown below.
Answer:
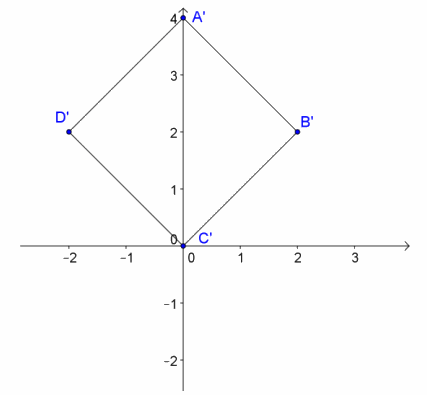
A’=4(cos(90°)+i sin(90°) )
B’=2\(\sqrt{2}\)(cos(45°)+i sin(45°) )
C’=0(cos(0°)+i sin(0°) )
D’=2\(\sqrt{2}\)(cos(135°)+i sin(135°) )
Question 11.
How do the modulus and argument of coordinate A in Problem 9 correspond to the modulus and argument of point A’ in Problem 10? Does a similar relationship exist when you compare B to B’, C to C’, and D to D’? Explain why you think this relationship exists.
Answer:
The modulus multiplied by a factor of 2\(\sqrt{2}\)and the argument is 45° more. The same is true when you compare B to B’ and D to D’. The relationship could also be true for C and C’, although the argument of C and C’ can really be any number since the modulus is 0.
Question 12.
Describe the transformations that map ABCD to A’B’C’D’.
Answer:
Rotate by 45° counterclockwise, and then dilate by a factor of 2\(\sqrt{2}\).
Eureka Math Precalculus Module 1 Lesson 13 Trigonometry Review: Additional Resources Answer Key
Question 1.
Evaluate the following.
a. sin(30°)
Answer:
\(\frac{1}{2}\)
b. cos(\(\frac{\pi}{3}\))
Answer:
\(\frac{1}{2}\)
c. sin(225°)
Answer:
–\(\frac{\sqrt{2}}{2}\)
d. cos(\(\frac{5π}{6}\))
Answer:
–\(\frac{\sqrt{3}}{2}\)
e. sin(\(\frac{5π}{3}\))
Answer:
–\(\frac{\sqrt{3}}{2}\)
f. cos(330°)
Answer:
\(\frac{\sqrt{3}}{2}\)
Question 2.
Solve for the acute angle θ, both in radians and degrees, in a right triangle if you are given the opposite side, O, and adjacent side, A. Round to the nearest thousandth.
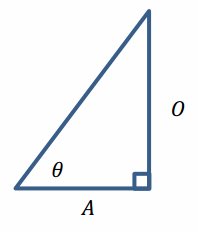
A. O=3 and A=4
Answer:
arctan(\(\frac{3}{4}\))≈0.644 radians=36.898°
B. O=6 and A=1
Answer:
arctan(\(\frac{6}{1}\))≈1.406 radians=80.558°
C. O=3\(\sqrt{3}\)and A=2
Answer:
arctan(\(\frac{3 \sqrt{3}}{2}\))≈1.203 radians=68.948°
Question 3.
Convert angles in degrees to radians, and convert angles in radians to degrees.
a. 150°
Answer:
\(\frac{5 \pi}{6}\)
b. \(\frac{4π}{3}\)
Answer:
240°
c. \(\frac{3π}{4}\)
Answer:
135°A