Engage NY Eureka Math Precalculus Module 1 Lesson 5 Answer Key
Eureka Math Precalculus Module 1 Lesson 5 Exercise Answer Key
Opening Exercise
Write down two fundamental facts about i that you learned in the previous lesson.
Answer:
Multiplication by i induces a 90-degree counterclockwise rotation about the origin. Also, i satisfies the equation
i2=-1.
Exercises 1–7
Exercise 1.
Give an example of a real number, an imaginary number, and a complex number. Use examples that have not already been discussed in the lesson.
Answer:
Answers will vary.
Exercise 2.
In the complex plane, what is the horizontal axis used for? What is the vertical axis used for?
Answer:
The horizontal axis is used to represent the real component of a complex number. The vertical axis is used to represent the imaginary component.
Exercise 3.
How would you represent -4+3i in the complex plane?
Answer:
The complex number -4+3i corresponds to the point (-4,3) in the coordinate plane.
For Exercises 4–7, let a=1+3i and b=2-i.
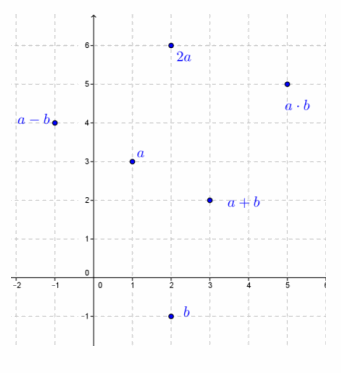
Exercise 4.
Find a+b. Then, plot a, b, and a+b in the complex plane.
Answer:
a+b=3+2i
Exercise 5.
Find a-b. Then, plot a, b, and a-b in the complex plane.
Answer:
a-b=-1+4i
Exercise 6.
Find 2a. Then, plot a and 2a in the complex plane.
Answer:
2a=2+6i
Exercise 7.
Find a∙b. Then, plot a, b, and a∙b in the complex plane.
Answer:
a∙b=(1+3i)(2-i)
=2-i+6i-3i2
=2+5i+3
=5+5i
Eureka Math Precalculus Module 1 Lesson 5 Problem Set Answer Key
Problems 1–4 involve the relationships among the set of real numbers, the set of imaginary numbers, and the set of complex numbers. Problems 5–9 involve practice with the core set of arithmetic skills from this lesson. Problems 10–12 involve the complex plane. A reproducible complex plane is provided at the end of the lesson should the teacher choose to hand out copies for the Problem Set.
Question 1.
The number 5 is a real number. Is it also a complex number? Try to find values of a and b so that 5=a+bi.
Answer:
Because 5=5+0i, 5 is a complex number.
Question 2.
The number 3i is an imaginary number and a multiple of i. Is it also a complex number? Try to find values of a and b so that 3i=a+bi.
Answer:
Because 3i=0+3i, 3i is a complex number.
Question 3.
Daria says that every real number is a complex number. Do you agree with her? Why or why not?
Answer;
For any real number a, a=a+0i, so Daria is correct.
Question 4.
Colby says that every imaginary number is a complex number. Do you agree with him? Why or why not?
Answer:
An imaginary number bi=0+bi, so Colby is correct.
In Problems 5–9, perform the indicated operations. Report each answer as a complex number w=a+bi, and graph it in a complex plane.
Question 5.
Given z1=-9+5i, z2=-10-2i, find w=z1+z2, and graph z1, z2, and w.
Answer:
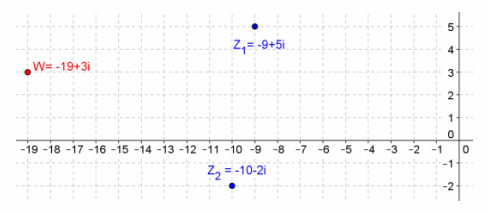
w=-19+3i
Question 6.
Given z1=-4+10i, z2=-7-6i, find w=z1-z2, and graph z1, z2, and w.
Answer:
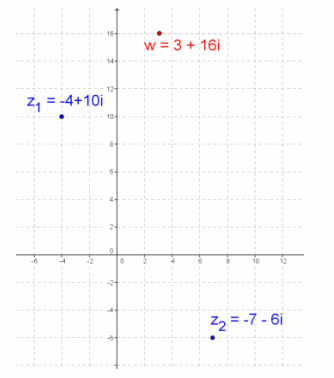
w=(-4+10i)-(-7-6i)
=3+16i
Question 7.
Given z1=3\(\sqrt{2}\)+2i, z2=\(\sqrt{2}\)-i, find w=z1-z2, and graph z1, z2, and w.
Answer:
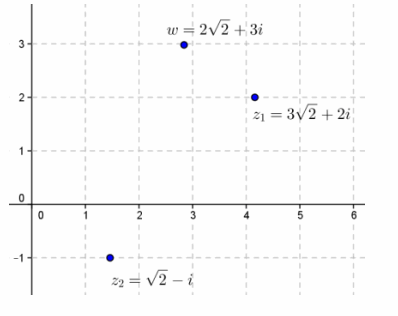
w=(3\(\sqrt{2}\)+2i)-(\(\sqrt{2}\)-i)
=2\(\sqrt{2}\)+3i
Question 8.
Given z1=3, z2=-4+8i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
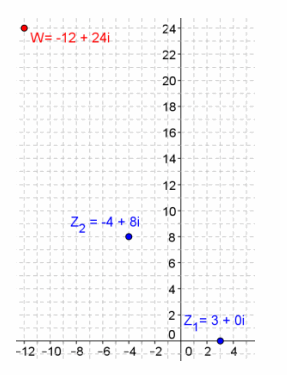
w=-12-24i
Question 9.
Given z1=\(\frac{1}{4}\), z2=12-4i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
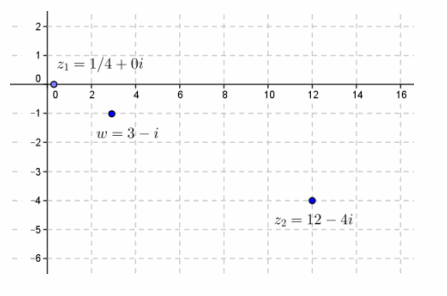
w=3-i
Question 10.
Given z1=-1, z2=3+4i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
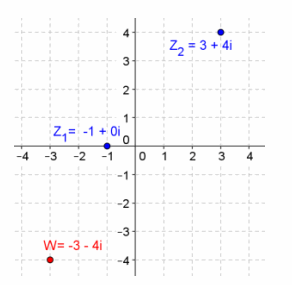
w=-3-4i
Question 11.
Given z1=5+3i, z2=-4-2i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
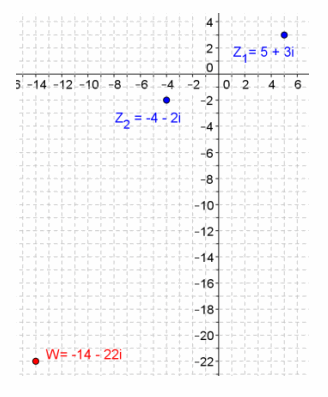
w=(5+3i)(-4-2i)
=-20-10i-12i-6i2
=-20-22i-6(-1)
=-14-22i
Question 12.
Given z1=1+i, z2=1+i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer
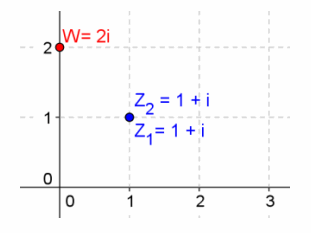
w=(1+i)(1+i)
=1+2i+i2
=1+2i-1
=2i
Question 13.
Given z1=3, z2=i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
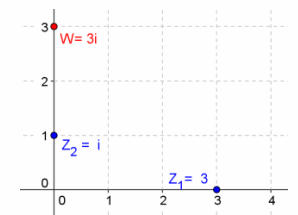
w=i ∙ 3
=3i
Question 14.
Given z1=4+3i, z2=i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
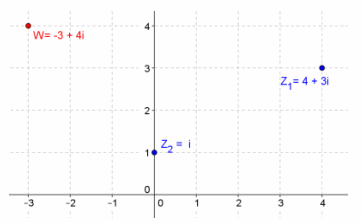
w=i(4+3i)
=-3+4i
Question 15.
Given z1=2\(\sqrt{2}\)+2\(\sqrt{2}\)i, z2=-\(\sqrt{2}\)+\(\sqrt{2}\) i, find w=z1 ∙ z2, and graph z1, z2, and w.
Answer:
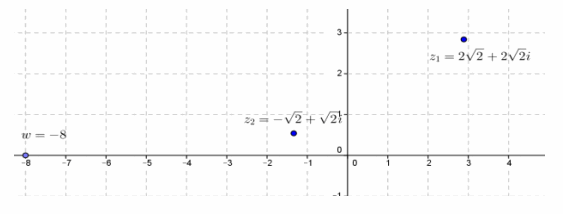
w=(2\(\sqrt{2}\)+2\(\sqrt{2}\) i)(-\(\sqrt{2}\)+\(\sqrt{2}\) i)
=-4+4i-4i-4
=-8
Question 16.
Represent w=-4+3i as a point in the complex plane.
Answer:
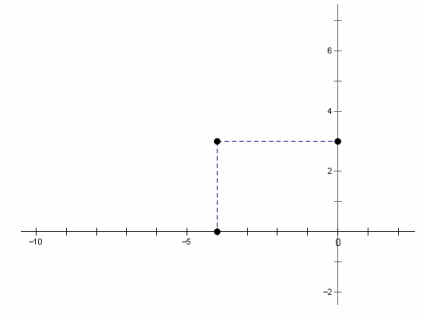
Question 17.
Represent 2w as a point in the complex plane. 2w=2(-4+3i)=-8+6i
Answer:
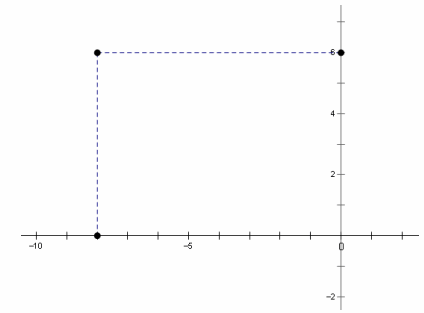
Question 18.
Compare the positions of w and 2w from Problems 10 and 11. Describe what you see. (Hint: Draw a segment from the origin to each point.)
Answer:
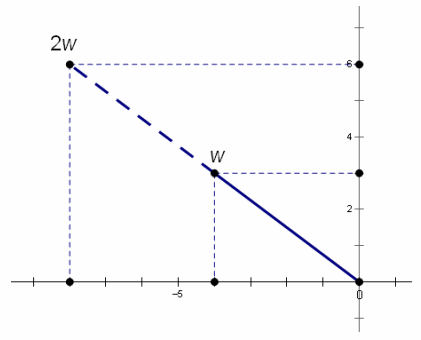
The points 0, w, and 2w all lie on the same line. The distance from 0 to 2w is twice as great as the distance from 0 to w. The segment to 2w is a scaled version of the segment to w, with scale factor 2.
Complex Plane Reproducible
Eureka Math Precalculus Module 1 Lesson 5 Exit Ticket Answer Key
In Problems 1–4, perform the indicated operations. Write each answer as a complex number a+bi.
Question 1.
Let z1=-2+i, z2=3-2i, and w=z1+z2. Find w, and graph z1, z2, and w in the complex plane.
Answer:
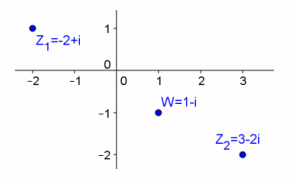
w=1-i
Question 2.
Let z1=-1-i, z2=2+2i, and w=z1-z2. Find w, and graph z1, z2, and w in the complex plane.
Answer:
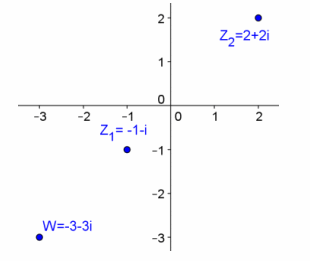
w=-3-3i
Question 3.
Let z=-2+i and w=-2z. Find w, and graph z and w in the complex plane.
Answer:
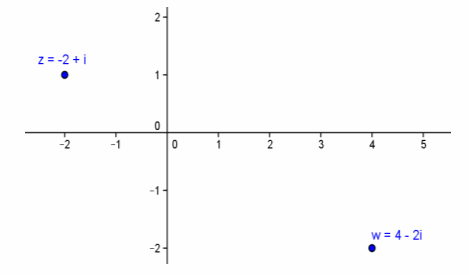
w=4-2i
Question 4.
Let z1=1+2i, z2=2-i, and w=z1 ∙ z2. Find w, and graph z1, z2, and w in the complex plane.
Answer:
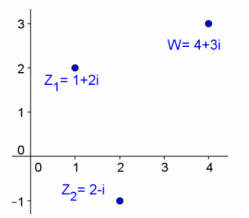
w=(1+2i)(2-i)
=2-i+4i+2
=4+3i