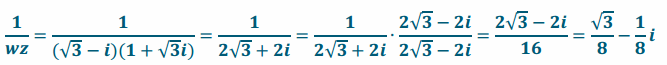Eureka Math Precalculus Module 1 Lesson 17 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 17 Answer Key

Eureka Math Precalculus Module 1 Lesson 17 Exercise Answer Key

Opening Exercise
Given w=1+i, what is arg⁡(w) and |w|? Explain how you got your answer.
Answer:
arg⁡(w)=\(\frac{π}{4}\) and |w|=\(\sqrt{2}\). I used the formula |w|=\(\sqrt{a^{2}+b^{2}}\) to determine the modulus, and since the point (1,1) lies along a ray from the origin that has been rotated 45° from the ray through the origin that contains the real number 1, the argument must be \(\frac{π}{4}\).

Eureka Math Precalculus Module 1 Lesson 17 Exploratory Challenge Answer Key

Students should complete the next nine exercises in small groups of three to four students. As teams work on these problems, circulate around the room to monitor progress. Some groups may get stuck on Exercise 3. Since the argument of a complex number on an interval 0≤arg⁡(z)<2π has been defined, students need to figure a positive rotation on this interval that is equivalent to -arg⁡(z). Lead a whole-class discussion at this point if needed before moving the groups on to complete the rest of the exercises in this Exploratory Challenge. After Exercise 6, have one or two students report their group’s response to this item.

Exploratory Challenge 1/Exercises 1–9

Exercise 1.
Describe the geometric effect of the transformation L(z)=(1+i)z.
Answer:
The transformation rotates the complex number about the origin through 45° and dilates the number by a scale factor of \(\sqrt{2}\).

Exercise 2.
Describe a way to undo the effect of the transformation L(z)=(1+i)z.
Answer:
Geometrically, we need to rotate in the opposite direction, -45°, and dilate by a factor of \(\frac{1}{\sqrt{2}}\).

Exercise 3.
Given that 0≤arg⁡(z)<2π for any complex number, how could you describe any clockwise rotation of θ as an argument of a complex number?
Answer:
arg⁡(z)=2π-θ would result in the same rotation as a clockwise rotation of θ.

Exercise 4.
Write a complex number in polar form that describes a rotation and dilation that will undo multiplication by (1+i), and then convert it to rectangular form.
Answer:
\(\frac{1}{\sqrt{2}}\) (cos⁡(315°)+ i sin⁡(315°)) = \(\frac{1}{\sqrt{2}}\)∙\(\frac{1}{\sqrt{2}}\)+i∙\(\frac{1}{\sqrt{2}}\)∙-\(\frac{1}{\sqrt{2}}\)=\(\frac{1}{2}\)–\(\frac{1}{2}\)i

Exercise 5.
In a previous lesson, you learned that to undo multiplication by 1+i, you would multiply by the reciprocal \(\frac{1}{1+i}\). Write the complex number \(\frac{1}{1+i}\) in rectangular form z=a+bi where a and b are real numbers.
Answer:
\(\frac{1}{1+i}\)=\(\frac{1-i}{(1+i)(1-i)}\)=\(\frac{1-i}{2}\)=\(\frac{1}{2}\)–\(\frac{1}{2}\) i

Exercise 6.
How do your answers to Exercises 4 and 5 compare? What does that tell you about the geometric effect of multiplication by the reciprocal of a complex number?
Answer:
The geometric effect of rotation by 2π-arg(z) and dilation by \(\frac{1}{|z|}\) appears to be the same as multiplication by the reciprocal when the problem is solved algebraically.

Exercise 7.
Jimmy states the following:
Multiplication by \(\frac{1}{a+b i}\) has the reverse geometric effect of multiplication by +bi.
Do you agree or disagree? Use your work on the previous exercises to support your reasoning.
Geometrically undoing the effect of multiplication by a+bi by rotating in the opposite direction by the argument and dilating by the reciprocal of the modulus gave us the same results as when we rewrote \(\frac{1}{a+b i}\) in rectangular form. This statement appears to be true. In each case, we got the same complex number.

Exercise 8.
Show that the following statement is true when z=2-2\(\sqrt{3}\)i:
The reciprocal of a complex number z with modulus r and argument θ is \(\frac{1}{z}\) with modulus \(\frac{1}{r}\) and argument 2π-θ.
Answer:
Since 2-2\(\sqrt{3}\)i has modulus 4 and argument \(\frac{5 \pi}{3}\), we must have

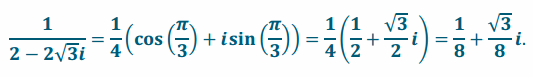
Multiplying by 1 using the conjugate, we have

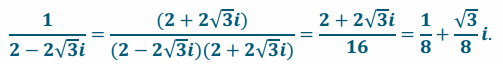
Since both methods produce equivalent complex numbers, this statement is true when z=2-2\(\sqrt{3}\)i.

Exercise 9.
Explain using transformations why z∙\(\frac{1}{z}\)=1.
Answer:
The complex number z can be thought of as a rotation of the real number 1 by arg(z) and a dilation by |z|. If we multiply this number by its reciprocal, then we rotate arg(z) in the opposite direction and dilate by a factor of \(\frac{1}{|z|}\). This will return the rotation to 0 and the modulus to 1, which describes the real number 1.

Exploratory Challenge 2/Exercise 10

Exercise 10.
Complete the graphic organizer below to summarize your work with complex numbers so far.

Answer:

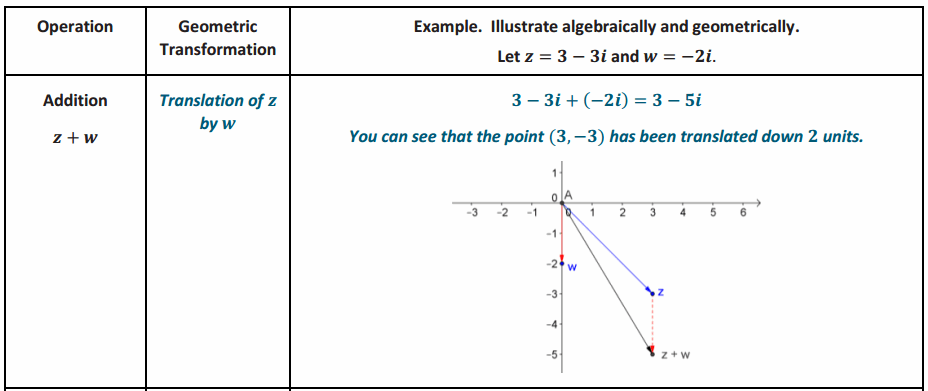
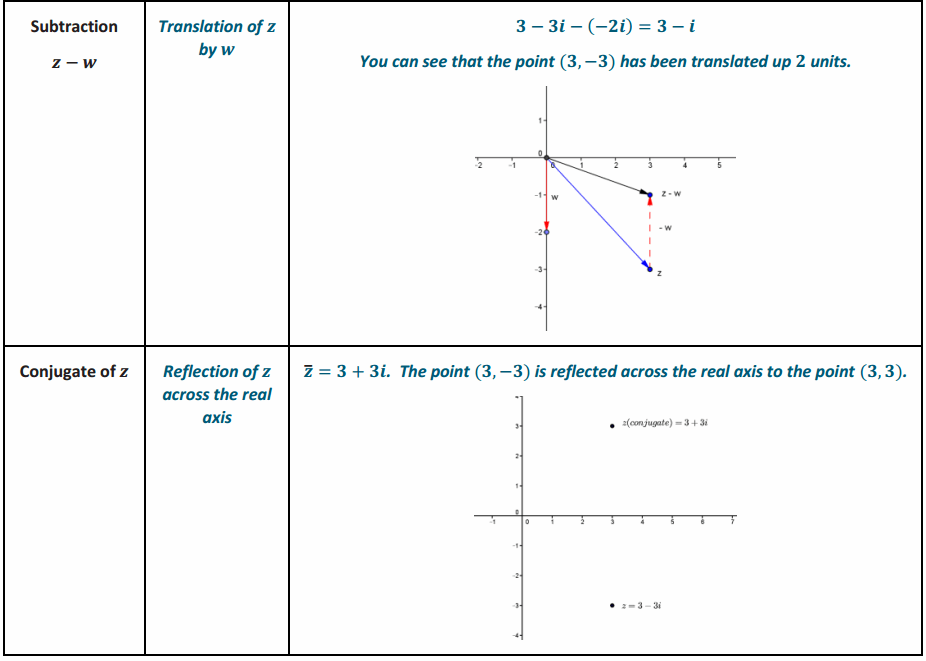
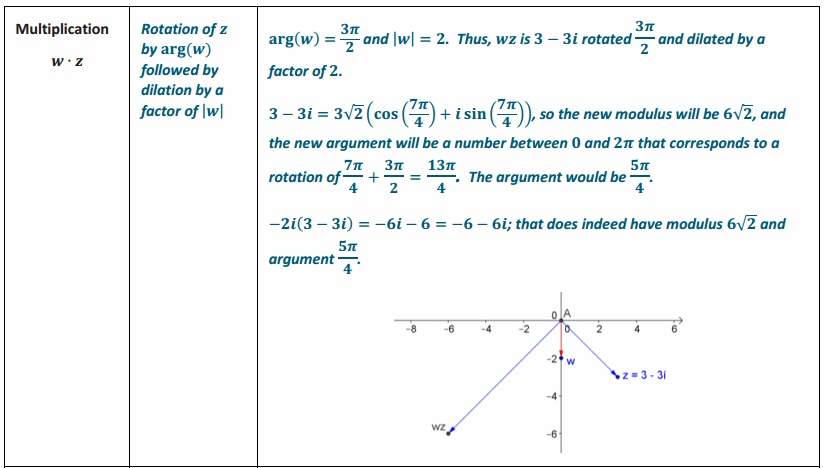
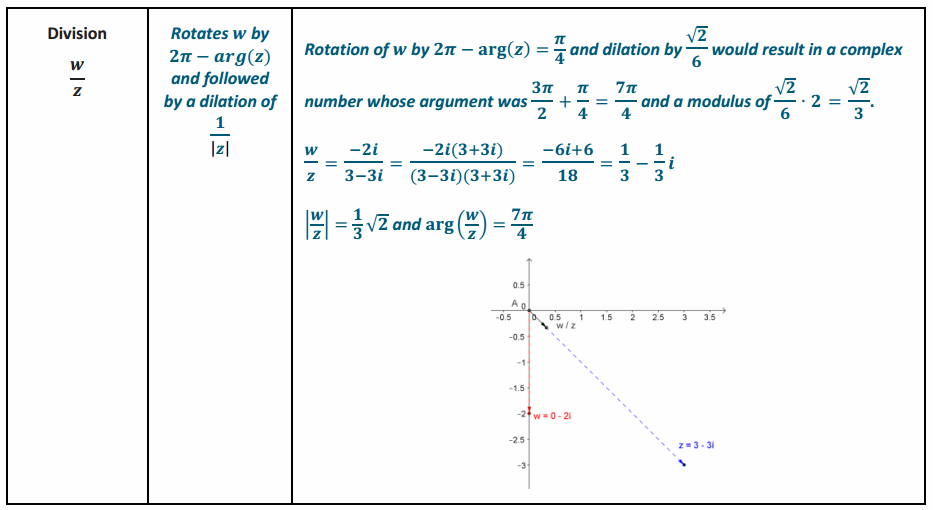
Exercises 11–13
Let z=-1+i, and let w=2i. Describe each complex number as a transformation of z, and then write the number in rectangular form.

Exercise 11.
w\(\overline{\mathbf{Z}}\)
Answer:
z is reflected across the real axis; then, that number is rotated by arg⁡(w) and dilated by |w|.
arg⁡(z)=\(\frac{3π}{4}\) and |z|=\(\sqrt{2}\). arg⁡(\(\overline{\mathbf{Z}}\))=\(\frac{5π}{4}\) with the same modulus as z. Rotation by arg⁡(w)=\(\frac{π}{2}\) and dilation by 2 would give a complex number with argument of 5\(\frac{π}{4}\)+\(\frac{π}{2}\)=7\(\frac{π}{4}\) and modulus of 2\(\sqrt{2}\), which is the modulus and argument of the number shown below.
w\(\overline{\mathbf{Z}}\)=2i(-1-i)=2-2i

Exercise 12.
\(\frac{1}{\bar{z}}\)
Answer:
z is reflected across the real axis and then rotated 2π-arg⁡(\(\overline{\mathbf{Z}}\)) and dilated by \(\frac{1}{|\overline{\mathbf{Z}}|}\). The result is a dilation of z.
Reflection of z across the real axis results in a complex number with argument \(\frac{5π}{4}\) and modulus of \(\sqrt{2}\). The reciprocal has argument 2π-\(\frac{5π}{4}\)=\(\frac{3π}{4}\) and modulus \(\frac{1}{\sqrt{2}}\)=\(\frac{\sqrt{2}}{2}\). This number has the same argument as z and is a dilation by a factor of \(\frac{1}{2}\).
\(\frac{1}{\bar{z}}\) = \(\frac{1}{-1-i}\)=\(\frac{-1+i}{(-1-i)(-1+i)}\)=\(\frac{-1+i}{2}\)=-\(\frac{1}{2}\)+\(\frac{i}{2}\)

Exercise 13.
\(\overline{w+z}\)
Answer:
z is translated by w vertically 2 units up since the real part of w is 0 and the imaginary part is 2. This new number is reflected across the real axis.
w+z=2i-1+i=-1+3i
\(\overline{w+z}\)=-1-3i

Eureka Math Precalculus Module 1 Lesson 17 Problem Set Answer Key

Question 1.
Describe the geometric effect of multiplying z by the reciprocal of each complex number listed below.

a. w₁=3i
Answer:
arg(w₁)=\(\frac{π}{2}\) and |w₁|=3
z is rotated by 2π-arg(w₁), which is 2π-\(\frac{π}{2}\)=\(\frac{3π}{2}\), and dilated by \(\frac{1}{3}\).

b. w₂=-2
Answer:
arg(w₂)=π and |w₂|=2
z is rotated by 2π-arg(w₂), which is 2π-π=π, and dilated by \(\frac{1}{2}\).

c. w₃=\(\sqrt{3}\)+i
Answer:
arg(w₃)=\(\frac{π}{6}\) and |w₃|=2
z is rotated by 2π-arg(w₃), which is 2π-\(\frac{π}{6}\)=\(\frac{11π}{6}\), and dilated by \(\frac{1}{2}\).

d. w₄=1-\(\sqrt{3}\)i
Answer:
arg(w₄)=\(\frac{5π}{3}\) and |w₄|=2
z is rotated by 2π-arg(w₄), which is 2π-(\(\frac{5π}{3}\))=\(\frac{π}{3}\), and dilated by \(\frac{1}{2}\).

Question 2.
Let z=-2-2\(\sqrt{3}\)i. Show that the geometric transformations you described in Problem 1 really produce the correct complex number by performing the indicated operation and determining the argument and modulus of each number.
a. \(\frac{-2-2 \sqrt{3} i}{w_{1}}\)
Answer:

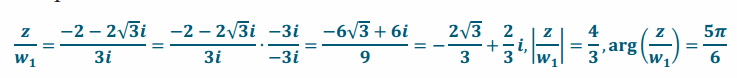
|z|=4, so the result of division is a complex number whose modulus is \(\frac{1}{3}\) of 4.
arg(z)=\(\frac{4π}{3}\), so the result of division by a complex number is whose argument represents the same rotation as \(\frac{4π}{3}\)+\(\frac{3π}{2}\)=\(\frac{17π}{6}\), which would be \(\frac{5π}{6}\).

b. \(\frac{-2-2 \sqrt{3} i}{w_{2}}\)
Answer:
\(\frac{-2-2 \sqrt{3} i}{-2}\) =\(\)=1+\(\sqrt{3}\)i,|\(\)|=2,arg(\(\))=\(\frac{π}{3}\)
|z|=4 and \(\frac{1}{2}\) of 4 is 2.
arg(z)=4\(\frac{π}{3}\), so the result of division will rotate z by –\(\frac{π}{2}\) and \(\frac{4π}{3}\)–\(\frac{π}{2}\)=\(\frac{5π}{6}\).

c. \(\frac{-2-2 \sqrt{3} i}{w_{3}}\)
Answer:

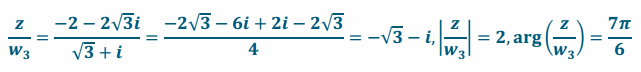
|z|=4 and \(\frac{1}{2}\) of 4 is 2.
arg(z)=4\(\frac{π}{3}\), so the result of division will rotate z by –\(\frac{π}{6}\) and \(\frac{4π}{3}\)–\(\frac{π}{6}\)=\(\frac{7π}{6}\).

d. \(\frac{-2-2 \sqrt{3} i}{w_{4}}\)
Answer:

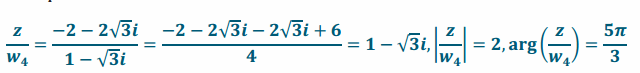
|z|=4, and \(\frac{1}{2}\) of 4 is 2.
arg(z)=\(\frac{4π}{3}\), so the result of division will rotate z by –\(\frac{5π}{3}\), and \(\frac{4π}{3}\)–\(\frac{5π}{3}\)=-\(\frac{π}{3}\). A rotation of –\(\frac{π}{3}\) will be the same as a rotation of \(\frac{5π}{3}\), which is the argument of the quotient.

Question 3.
In Exercise 12 of this lesson, you described the complex number \(\frac{1}{\bar{z}}\) as a transformation of z for a specific complex number z. Show that this transformation always produces a dilation of z=a+bi.
Answer:
\(\overline{\mathbf{z}}\)=a-bi, and \(\frac{1}{a-b i}\)=\(\frac{1}{a-b i}\)∙\(\frac{a+b i}{a+b i}\)=\(\frac{a+b i}{a^{2}+b^{2}}\)=\(\frac{1}{a^{2}+b^{2}}\)(a+bi). This complex number is the product of a real number and the original complex number z, so it will have the same argument as a+bi, but the modulus will be a different number.

Question 4.
Does L(z)=\(\frac{1}{z}\) satisfy the conditions that L(z+w)=L(z)+L(w) and L(mz)=mL(z), which makes it a linear transformation? Justify your answer.
Answer:
\(\frac{1}{z}\)=\(\frac{1}{a+b i}\)=\(\frac{a-b i}{a^{2}+b^{2}}\), which is a complex number whose real part is \(\frac{a}{a^{2}+b^{2}}\) and whose imaginary part is –\(\frac{b}{a^{2}+b^{2}}\). Since all complex numbers satisfy the conditions that make them a linear transformation, and \(\frac{1}{z}\) is a complex number, it will also be a linear transformation.

Question 5.
Show that L(z)=w((\(\frac{\overline{1}}{w} z\)) describes a reflection of z about the line containing the origin and w for z=3i and w=1+i.
Answer:
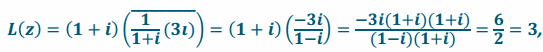, which is the image of the transformation z that is reflected about the line containing the origin and w.

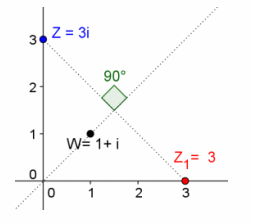
Question 6.
Describe the geometric effect of each transformation function on z where z, w, and a are complex numbers.

a. L₁(z)=\(\frac{z-w}{a}\)
Answer:
z is translated by w, rotated by 2π-arg(a), and dilated by \(\frac{1}{|a|}\).

b. L₂(z)=\(\overline{\left(\frac{Z-W}{a}\right)}\)
Answer:
z is translated by w, reflected about the real axis, rotated by 2π-arg(a), and dilated by \(\frac{1}{|a|}\), and reflected about the real axis.

c. L₃(z)=a(\(\overline{\left(\frac{Z-W}{a}\right)}\))
Answer:
z is translated by w, reflected about the real axis, rotated by 2π-arg(a), and dilated by \(\frac{1}{|a|}\), and reflected about the real axis, rotated by arg(a), and dilated by |a|.

d. L₃(z)=a(\(\overline{\left(\frac{z-w}{a}\right)}\)) +w
Answer:
z is translated by w, reflected about the real axis, rotated by 2π-arg(a), and dilated by \(\frac{1}{|a|}\), and reflected about the real axis, rotated by arg(a), dilated by |a|, and translated by w.

Question 7.
Verify your answers to Problem 6 if z=1-i, w=2i, and a=-1-i.
a. L₁(z)=\(\frac{z-w}{a}\)
Answer:
|z|=\(\sqrt{2}\),arg(z)=7\(\frac{π}{4}\),|w|=2,arg(w)=π,|a|=\(\sqrt{2}\),arg(a)=5\(\frac{π}{4}\)=3.927

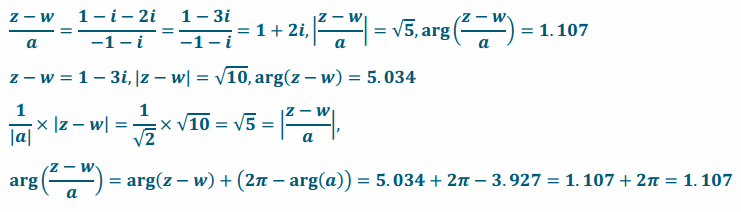
b. L₂(z)=\(\overline{\left(\frac{Z-W}{a}\right)}\)
Answer:

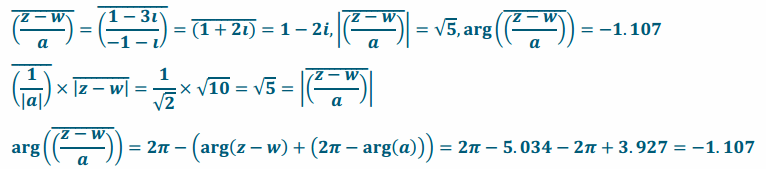
c. L₃(z)=a(\(\overline{\left(\frac{Z-W}{a}\right)}\))+w
Answer:

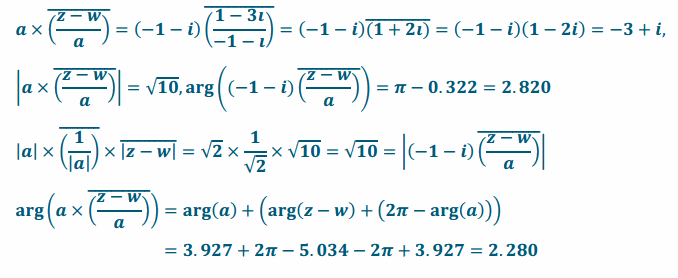
d. L₃ (z) = a(\(\overline{\left(\frac{Z-W}{a}\right)}\)) + w
Answer:

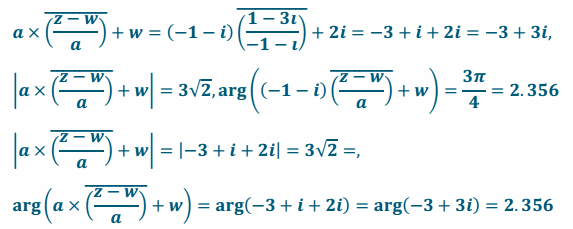
Eureka Math Precalculus Module 1 Lesson 17 Exit Ticket Answer Key

Let z=1+\(\sqrt{3}\)i and w=\(\sqrt{3}\)-i. Describe each complex number as a transformation of z, and then write the number in rectangular form, and identify its modulus and argument.

Question 1.
\(\frac{\boldsymbol{z}}{\boldsymbol{w}}\)
Answer:
z is rotated by -arg⁡(w) and dilated by \(\frac{1}{|w|}\).
arg⁡(z)=\(\frac{π}{3}\) and 2π-arg⁡(w)=2π-\(\frac{11π}{6}\)=\(\frac{π}{6}\). So, division by w should rotate z to \(\frac{π}{2}\). |z|=2, and 1/|w| =\(\frac{1}{2}\), so the modulus of \(\frac{z}{3}\) should be 2∙\(\frac{1}{2}\)=1. This rotation and dilation describe the complex number i. Algebraically, we get the same number.
\(\frac{z}{3}\)=\(\frac{1+\sqrt{3} i}{\sqrt{3}-i}\)=\(\frac{1+\sqrt{3}}{\sqrt{3}-i}\)∙\(\frac{\sqrt{3}+i}{\sqrt{3}+i}\)=\(\frac{4 i}{4}\)=i

Question 2.
\(\frac{1}{wz}\)
Answer:
z is rotated arg(w) and dilated by |w| and then rotated -arg(wz) and dilated by \(\frac{1}{|w z|}\). For the given values of z and w, this transformation results in a dilation of w by a factor of \(\frac{1}{4}\).
arg⁡(z)=\(\frac{π}{3}\) and arg⁡(w)=\(\frac{11π}{6}\). Adding these arguments and finding an equivalent rotation between 0 and 2π gives a rotation of \(\frac{π}{6}\) and |wz|=2∙2=4. This describes the complex number 2\(\sqrt{3}\)+2i. The reciprocal of this number has argument \(\frac{11π}{6}\) and modulus \(\frac{1}{4}\), which describes the complex number \(\frac{\sqrt{3}}{8}\)–\(\frac{1}{8}\)i.