Engage NY Eureka Math 8th Grade Module 7 Lesson 11 Answer Key
Eureka Math Grade 8 Module 7 Lesson 11 Example Answer Key
Example 1.
Consider the decimal expansion of \(\sqrt{3}\).
Find the first two values of the decimal expansion using the following fact: If c2 < 3 < d2 for positive numbers c and d, then c < \(\sqrt{3}\) < d.
First approximation: Because 1 <3 < 4, we have 1 < \(\sqrt{3}\) < 2.
Answer:
We learned in Lesson 3 that if c and d are positive numbers, then c2 < d2 implies c2 < d2. It follows from this that if c2 < N < d2, then c<\(\sqrt{N}\) c < \(\sqrt{N}\) < d, then c2 < N < d2.)
Since 1 < 3 < 4, we get our first approximation: 1 < \(\sqrt{3}\) < 2.
To get more precise with our estimate of \(\sqrt{3}\), we can look at the tenths between the numbers 1 and 2.
Second approximation:
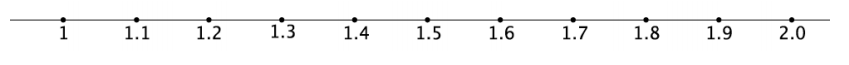
Answer:
→ Is \(\sqrt{3}\) between 1.2 and 1.3?
→ If 1.2 < \(\sqrt{3}\) < 1.3, then we should have 1.22 < 3 < 1.32. But we don’t: 1.22 = 1.44 and 1.32 = 1.69. These squares are too small.
→ Is \(\sqrt{3}\) between 1.8 and 1.9?
If 1.8 < \(\sqrt{3}\) < 1.9, then we should have 1.82<3<1.92. But we don’t: 1.82 = 3.24 and 1.92 = 3.81. These squares are too large.
→ Can you find the right tenth interval in which \(\sqrt{3}\) belongs?
After some trial and error, students see that \(\sqrt{3}\) lies between 1.7 and 1.8 . We have 1.72 = 2.89 and 1.82 = 3.24, and so 2.89 < 3 < 3.24.
So the decimal expansion of \(\sqrt{3}\) begins 1.7…. How could we pin down its next decimal place?
Look for where \(\sqrt{3}\) lies in the interval between 1.7 and 1.8. Divide that interval into ten parts, too.
Let’s do that!
Third approximation:

Answer:
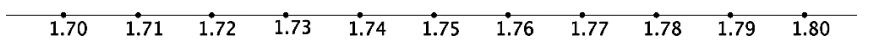
Have students use trial and error to eventually establish that \(\sqrt{3}\) lies between 1.73 and 1.74: we have 1.732 = 2.9929 and 1.742 = 3.0276 and 2.9926 < 3 < 3.0276.
→ So what are the first two places of the decimal expansion of \(\sqrt{3}\)?
We have \(\sqrt{3}\) = 1.73….
→ What do you think will need to be done to get an even more precise estimate of the number \(\sqrt{3}\)?
We will need to look at the interval between 1.73 and 1.74 more closely and repeat the process we did before.
→ Would you like to find the next decimal place for \(\sqrt{3}\) just for fun or leave it be for now?
Give students the option to find the next decimal place if they wish.
How accurate is our approximation \(\sqrt{3}\) = 1.73…? (If students computed
\(\sqrt{3}\) = 1.732…, adjust this question and the answer below appropriately.)
We know \(\sqrt{3}\) = 1.73abc… for some more digits a, b, c, and so on. Now 1.73 and 1.73abc… differ by 0.00abc…, which is less than 0.01. A decimal expansion computed to two decimal places gives an approximation that is accurate with an error that is at most 0.01.
Example 2.
Find the first few places of the decimal expansion of \(\sqrt{28}\).
First approximation:
Answer:
Between which two integers does \(\sqrt{28}\) lie?
Since 25 < 28 < 36, we see 5 < \(\sqrt{28}\) < 6 .
In which tenth between 5 and 6 does \(\sqrt{28}\) lie?
Second approximation:

Answer:
How do we determine which interval is correct?
What if we just square the numbers 5.0, 5.1, and 5.2 and see between which two squares 28 lies? After all, we are hoping to see that 5.3 < \(\sqrt{28}\) < 5.4, in which case we should have 5.32 < 28 <5 .42. (This interval is probably not correct, but we can check!)
Provide students time to determine in which interval the number \(\sqrt{28}\) lies. Ask students to share their findings, and then continue the discussion.
Now that we know that the number \(\sqrt{28}\) lies between 5.2 and 5.3, let’s look at hundredths.
Third approximation:

Answer:

Can we be efficient? Since 5.202 = 27.04 and 5.302 = 28.09, would an interval to the left, to the middle, or to the right likely contain \(\sqrt{28}\)?
We suspect that the interval between 5.29 and 5.30 might contain \(\sqrt{28}\) because 28 is close to 28.09.
Provide students time to determine which interval the number \(\sqrt{28}\) will lie between. Ask students to share their findings, and then continue the discussion.
Now we know that the number \(\sqrt{28}\) is between 5.29 and 5.30. Let’s go one step further and examine intervals of thousandths.
Fourth approximation:

Answer:

Since 5.2902 = 27.9841 and 5.3002 = 28.09, where should we begin our search?
We should begin with the intervals closer to 5.290 and 5.291 because 28 is closer to 27.9841 than to 28.09.
Provide students time to determine which interval the number \(\sqrt{28}\) will lie between. Ask students to share their findings, and then finish the discussion.
The number \(\sqrt{28}\) lies between 5.291 and 5.292 because 5.2912 = 27.994681 and 5.2922 = 28.005264. At this point, we have a fair approximation of the value of \(\sqrt{28}\). It is between 5.291 and 5.292 on the number line:

We could continue this process of rational approximation to see that \(\sqrt{28}\) = 5.291502622….
As before, use an online calculator to show the decimal expansion of \(\sqrt{28}\). Once displayed, ask students to examine the decimal expansion for any patterns, or lack thereof
Consider going back to the Opening Exercise to determine whose approximation was the closest.
Can we conduct this work to also pin down the location of \(\sqrt{121}\) on the number line?
No need! \(\sqrt{121}\) = 11, so we know where it sits!
Eureka Math Grade 8 Module 7 Lesson 11 Exercise Answer Key
Exercise 1.
In which interval of hundredths does \(\sqrt{14}\) lie? Show your work.
Answer:
The number \(\sqrt{14}\) is between integers 3 and 4 because 9<14<16. Then, \(\sqrt{14}\) must be checked for the interval of tenths between 3 and 4. Since \(\sqrt{14}\) is closer to 4, we will begin with the interval from 3.9 to 4.0. The number \(\sqrt{14}\) is between 3.7 and 3.8 because 3.72 = 13.69 and 3.82 = 14.44. Now, we must look at the interval of hundredths between 3.7 and 3.8. Since \(\sqrt{14}\) is closer to 3.7, we will begin with the interval 3.70 to 3.71. The number \(\sqrt{14}\) is between 3.74 and 3.75 because 3.742 = 13.9876 and 3.752 = 14.0625.
Eureka Math Grade 8 Module 7 Lesson 11 Problem Set Answer Key
Question 1.
In which hundredth interval of the number line does \(\sqrt{84}\) lie?
Answer:
The number \(\sqrt{84}\) is between 9 and 10 but closer to 9. Looking at the interval of tenths, beginning with 9.0 to 9.1, the number \(\sqrt{84}\) lies between 9.1 and 9.2 because 9.12 = 82.81 and 9.22 = 84.64 but is closer to 9.2. In the interval of hundredths, the number \(\sqrt{84}\) lies between 9.16 and 9.17 because 9.162 = 83.9056 and 9.172 = 84.0889.
Question 2.
Determine the three-decimal digit approximation of the number \(\sqrt{34}\).
Answer:
The number \(\sqrt{34}\) is between 5 and 6 but closer to 6. Looking at the interval of tenths, beginning with 5.9 to 6.0, the number \(\sqrt{34}\) lies between 5.8 and 5.9 because 5.82 = 33.64 and 5.92 = 34.81 and is closer to 5.8. In the interval of hundredths, the number \(\sqrt{34}\) lies between 5.83 and 5.84 because 5.832 = 33.9889 and 5.842 = 34.1056 and is closer to 5.83. In the interval of thousandths, the number \(\sqrt{34}\) lies between 5.830 and 5.831 because 5.8302 = 33.9889 and 5.8312 = 34.000 561 but is closer to 5.831. Since 34 is closer to 5.8312 than 5.8302, then the three-decimal digit approximation of the number is 5.831.
Question 3.
Write the decimal expansion of \(\sqrt{47}\) to at least two-decimal digits.
Answer:
The number \(\sqrt{47}\) is between 6 and 7 but closer to 7 because 62<47<72. In the interval of tenths, the number \(\sqrt{47}\) is between 6.8 and 6.9 because 6.82 = 46.24 and 6.92 = 47.61. In the interval of hundredths, the number \(\sqrt{47}\) is between 6.85 and 6.86 because 6.852 = 46.9225 and 6.862 = 47.0596. Therefore, to two-decimal digits, the number \(\sqrt{47}\) is approximately 6.85
Question 4.
Write the decimal expansion of \(\sqrt{46}\) to at least two-decimal digits.
Answer:
The number \(\sqrt{46}\) is between integers 6 and 7 because 62<46<72. Since \(\sqrt{46}\) is closer to 7, I will start checking the tenths intervals between 6.9 and 7. \(\sqrt{46}\) is between 6.7 and 6.8 since 6.72 = 44.89 and 6.82 = 46.24. Checking the hundredths interval, \(\sqrt{46}\) is between 6.78 and 6.79 since 6.782 = 45.9684 and 6.792 = 46.1041. The two-decimal approximation \(\sqrt{46}\) is 6.78.
Question 5.
Explain how to improve the accuracy of the decimal expansion of an irrational number.
Answer:
In order to improve the accuracy of the decimal expansion of an irrational number, you must examine increasingly smaller increments on the number line. Specifically, examine increments of decreasing powers of 10. The basic inequality allows us to determine which interval a number is between. We begin by determining which two integers the number lies between and then decreasing the power of 10 to look at the interval of tenths. Again using the basic inequality, we can narrow down the approximation to a specific interval of tenths. Then, we look at the interval of hundredths and use the basic inequality to determine which interval of hundredths the number would lie between. Then, we examine the interval of thousandths. Again, the basic inequality allows us to narrow down the approximation to thousandths. The more intervals we examine, the more accurate the decimal expansion of an irrational number will be.
Question 6.
Is the number \(\sqrt{144}\) rational or irrational? Explain.
Answer:
The number \(\sqrt{144}\) is 12, a rational number.
Question 7.
Is the number \(0 . \overline{64}\) = 0.646464646… rational or irrational? Explain.
Answer:
We have seen that every number that has a repeating decimal expansion is a fraction; that is, it is a rational number. In this case, 0.646 464 646… = \(\frac{64}{99}\), and is therefore a rational number.
Question 8.
Henri computed the first 100 decimal digits of the number \(\frac{652}{541}\) and got 0.650646950092421441774491682070240295748613678373382624768946
39556377079482439926062846580406654343807763401109057301294….
He saw no repeating pattern to the decimal and so concluded that the number is irrational. Do you agree with Henri’s conclusion? If not, what would you say to Henri?
Answer:
The fraction \(\frac{352}{541}\) is certainly a rational number, and so it will have a repeating decimal expansion. One probably has to go beyond 100 decimal places to see the digits repeat.
(This decimal actually repeats after the 540th decimal place.)
Question 9.
Use a calculator to determine the decimal expansion of \(\sqrt{35}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{35}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.
Question 10.
Use a calculator to determine the decimal expansion of \(\sqrt{101}\). Does the number appear to be rational or irrational? Explain.
Based on the decimal expansion, the number \(\sqrt{101}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.
Question 11.
Use a calculator to determine the decimal expansion of \(\sqrt{7}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{7}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.
Question 12.
Use a calculator to determine the decimal expansion of \(\sqrt{8720}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{8720}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.
Question 13.
Use a calculator to determine the decimal expansion of \(\sqrt{17956}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{17956}\) is rational because it is equivalent to 134.
Question 14.
Since the number \(\frac{3}{5}\) is rational, must the number (3/5)2be rational as well? Explain.
Answer:
Yes, since \(\frac{3}{5}\) is rational it makes sense that (\(\frac{3}{5}\))2would also be rational since (\(\frac{3}{5}\))2 = \(\frac{9}{25}\) is a ratio of integers.
Question 15.
If a number x is rational, must the number x2 be rational as well? Explain.
Answer:
If x is rational, then we can write x = \(\frac{a}{b}\) for some integers a and b. This means that x2 = \(\frac{a^{2}}{b^{2}}\) and so is necessarily rational as well.
Question 16.
Challenge: Determine the two-decimal digit approximation of the number \(\sqrt [ 3 ]{ 9 }\).
Answer:
The number \(\sqrt [ 3 ]{ 9 }\) is between integers 2 and 3 because 23<9<33. Since \(\sqrt [ 3 ]{ 9 }\) is closer to 2, I will start checking the tenths intervals between 2 and 3. \(\sqrt [ 3 ]{ 9 }\) is between 2 and 2.1 since 23 = 8 and 2.13 = 9.261. Checking the hundredths interval, \(\sqrt [ 3 ]{ 9 }\) is between 2.08 and 2.09 since 2.083 = 8.998912 and 2.093 = 9.129329. The two-decimal digit approximation \(\sqrt [ 3 ]{ 9 }\) is 2.08.
Eureka Math Grade 8 Module 7 Lesson 11 Exit Ticket Answer Key
Question 1.
Determine the three-decimal digit approximation of the number \(\sqrt{17}\).
Answer:
The number \(\sqrt{17}\) is between integers 4 and 5 because 16<17<25. Since \(\sqrt{17}\) is closer to 4, I will start checking the tenths intervals closer to 4. \(\sqrt{17}\) is between 4.1 and 4.2 since 4.12 = 16.81 and 4.22 = 17.64. Checking the hundredths interval, \(\sqrt{17}\) is between 4.12 and 4.13 since 4.122 = 16.9744 and 4.132 = 17.0569. Checking the thousandths interval, \(\sqrt{17}\) is between 4.123 and 4.124 since 4.1232 = 16.999129 and 4.1242 = 17.007376.
The three-decimal digit approximation is 4.123.