Engage NY Eureka Math 8th Grade Module 7 Lesson 12 Answer Key
Eureka Math Grade 8 Module 7 Lesson 12 Example Answer Key
Example 1.
Find the decimal expansion of \(\frac{35}{11}\).
Answer:
For fun, let’s see if we can find the decimal expansion of \(\frac{35}{11}\) without using long division.
To start, can we say between which two integers this number lies?

The number \(\frac{35}{11}\) would lie between 3 and 4 on the number line because \(\frac{35}{11}\) = \(\frac{33}{11}\) + \(\frac{2}{11}\) = 3 + \(\frac{2}{11}\).
Could we say in which tenth between 3 and 4 the number 3 + \(\frac{2}{11}\) lies? Is this tricky?
We know that \(\frac{35}{11}\) has a decimal expansion beginning with 3 in the ones place because \(\frac{35}{11}\) = 3 + \(\frac{2}{11}\). Now we want to determine the tenths digit, the hundredths digit, and then the thousandths digit.

Ones Tenths Hundredths Thousandths
To figure out the tenths digit, we will use an inequality based on tenths. We are looking for the consecutive integers, m and m + 1, so that
3 + \(\frac{m}{10}\) < \(\frac{35}{11}\) < 3 + \(\frac{m + 1}{10}\) .

We can rewrite the middle term:
3 + \(\frac{m}{10}\) < 3 + \(\frac{2}{11}\) < 3 + \(\frac{m + 1}{10}\) .
This means we’re looking at
\(\frac{m}{10}\) < \(\frac{2}{11}\) < \(\frac{m + 1}{10}\).
Give students time to make sense of the inequalities 3 + \(\frac{m}{10}\) < \(\frac{35}{11}\) < 3 + \(\frac{m + 1}{10}\) and \(\frac{m}{10}\) < \(\frac{2}{11}\) < \(\frac{m + 1}{10}\).
Since the intervals of tenths are represented by \(\frac{m}{10}\) and \(\frac{m + 1}{10}\), consider using concrete numbers. The chart below may help students make sense of the intervals and the inequalities.
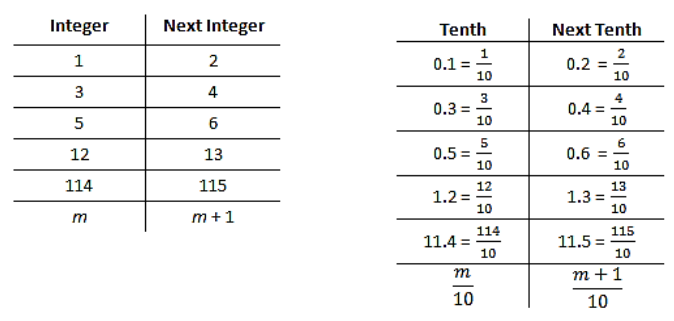
Eureka Math Grade 8 Module 7 Lesson 12 Exercise Answer Key
Exercises 1–3
Exercise 1.
Find the decimal expansion of \(\frac{5}{3}\) without using long division.
Answer:
\(\frac{5}{3}\) = \(\frac{3}{3}\) + \(\frac{2}{3}\)
= 1 + \(\frac{2}{3}\)
The decimal expansion begins with the integer 1.
Among the intervals of tenths, we are looking for integers m and m + 1 so that
1 + \(\frac{m}{10}\) < 1 + \(\frac{2}{3}\) < 1 + \(\frac{m + 1}{10}\),
which is the same as
\(\frac{m}{10}\) < \(\frac{2}{3}\) < \(\frac{m + 1}{10}\)
m < \(\frac{20}{3}\) < m + 1
and
\(\frac{20}{3}\) = \(\frac{18}{3}\) + \(\frac{2}{3}\)
= 6 + \(\frac{2}{3}\).
The tenths digit is 6.
Among the intervals of hundredths we are looking for integers m and m + 1 so that
1 + \(\frac{6}{10}\) + \(\frac{m}{100}\) < \(\frac{5}{3}\) < 1 + \(\frac{6}{10}\) + \(\frac{m + 1}{10}\) ,
which is equivalent to
\(\frac{m}{100}\) < \(\frac{2}{3}\) – \(\frac{6}{10}\) < \(\frac{m + 1}{10}\).
Now
\(\frac{2}{3}\) – \(\frac{6}{10}\) = \(\frac{2}{30}\) .
So we are looking for integers m and m + 1 where
\(\frac{m}{100}\) < \(\frac{2}{30}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{20}{3}\) < m + 1 .
But we already know that \(\frac{20}{3}\) = 6 + \(\frac{2}{3}\); therefore, the hundredths digit is 6. We feel like we are repeating our work, so we suspect \(\frac{5}{3}\) = 1.666″…” . To check: 0.6666″…” = 6/9 = \(\frac{2}{3}\) and 1.6666″…” = 1 + \(\frac{2}{3}\) = \(\frac{5}{3}\). We are correct.
Exercise 2.
Find the decimal expansion of \(\frac{5}{11}\) without using long division.
Answer:
Its decimal expansion begins with the integer 0.
In the intervals of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{5}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{50}{11}\) < m + 1
\(\frac{50}{11}\) = \(\frac{44}{11}\) + \(\frac{6}{11}\)
= 4 + \(\frac{6}{11}\)
The tenths digit is 4.
In the intervals of hundredths, we are looking for integers m and m + 1 so that

As
\(\frac{60}{11}\) = \(\frac{55}{11}\) + \(\frac{5}{11}\)
= 5 + \(\frac{5}{11}\)
we see that the hundredths digit is 5.
The fraction \(\frac{5}{11}\) has reappeared, which makes us suspect we are in a repeating pattern and we have
\(\frac{5}{11}\) = 0.454545″…” . To check: 0.454545″…” = \(\frac{45}{99}\) = \(\frac{5}{11}\). We are correct.
Exercise 3.
Find the decimal expansion of the number \(\frac{23}{99}\) first without using long division and then again using long division.
Answer:
The decimal expansion begins with the integer 0.
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{23}{99}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{230}{99}\) < m + 1.
Now
\(\frac{230}{99}\) = \(\frac{198}{99}\) + \(\frac{32}{99}\)
= 2 + \(\frac{32}{99}\)
showing that the tenths digit is 2.
In the interval of hundredths, we are looking for integers m and m + 1 so that
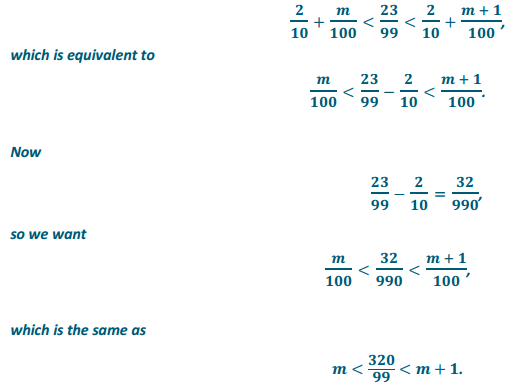
Now
\(\frac{320}{99}\) = \(\frac{297}{99}\) + \(\frac{23}{99}\)
= 3 + \(\frac{23}{99}\)
The hundredths digit is 3. The reappearance of 23/99 makes us suspect that we’re in a repeating pattern and \(\frac{23}{99}\) = 0.232323″…” . We check that 0.232323″…” does indeed equal \(\frac{23}{99}\) , and we are correct.
Eureka Math Grade 8 Module 7 Lesson 12 Problem Set Answer Key
Question 1.
Without using long division, explain why the tenths digit of \(\frac{3}{11}\) is a 2.
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{3}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{30}{11}\) < m + 1
\(\frac{30}{11}\) = \(\frac{22}{11}\) + \(\frac{8}{11}\)
= 2 + \(\frac{8}{11}\)
In looking at the interval of tenths, we see that the number \(\frac{3}{11}\) must be between \(\frac{2}{10}\) and \(\frac{3}{10}\)because \(\frac{2}{10}\) < \(\frac{3}{11}\) < \(\frac{3}{10}\). For this reason, the tenths digit of the decimal expansion of \(\frac{3}{11}\) must be 2.
Question 2.
Find the decimal expansion of \(\frac{25}{9}\) without using long division.
Answer:
\(\frac{25}{9}\) = \(\frac{18}{9}\) + \(\frac{7}{9}\)
= 2 + \(\frac{7}{9}\)
The ones digit is 2. In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{7}{9}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{70}{9}\) < m + 1
\(\frac{70}{9}\) = \(\frac{63}{9}\) + \(\frac{7}{9}\)
= 7 + \(\frac{7}{9}\)
The tenths digit is 7. The difference between \(\frac{7}{9}\) and \(\frac{7}{10}\) is
\(\frac{7}{9}\) – \(\frac{7}{10}\) = \(\frac{7}{90}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{7}{90}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{70}{9}\) < m + 1.
However, we already know that \(\frac{70}{9}\) = 7 + \(\frac{7}{9}\); therefore, the hundredths digit is 7. Because we keep getting \(\frac{7}{9}\), we can assume the digit of 7 will continue to repeat. Therefore, the decimal expansion of \(\frac{25}{9}\) is 2.777….
Question 3.
Find the decimal expansion of \(\frac{11}{41}\) to at least 5 digits without using long division.
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{11}{41}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{110}{41}\) < m + 1
\(\frac{110}{41}\) = \(\frac{82}{41}\) + \(\frac{28}{41}\) = 2 + \(\frac{28}{41}\).
The tenths digit is 2. The difference between \(\frac{11}{41}\) and \(\frac{2}{10}\) is
\(\frac{11}{41}\) – \(\frac{2}{10}\) = \(\frac{28}{410}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{28}{410}\) < \(\frac{m + 1}{100}\),
which is the same as

In the interval of ten – thousandths, we are looking for integers m and m + 1 so that

The hundred – thousandths digit is 9. We see again the fraction \(\frac{11}{41}\), so we can expect the decimal digits to repeat at this point. Therefore, the decimal approximation of \(\frac{11}{1}\) is 0.2682926829….
Question 4.
Which number is larger, \(\sqrt{10}\) or \(\frac{28}{9}\)? Answer this question without using long division.
Answer:
The number \(\sqrt{10}\) is between 3 and 4. In the sequence of tenths, \(\sqrt{10}\) is between 3.1 and 3.2 because
3.12 < (\(\sqrt{10}\))2 < 3.22. In the sequence of hundredths, \(\sqrt{10}\) is between 3.16 and 3.17 because
3.162 < (\(\sqrt{10}\))2 < 3.172. In the sequence of thousandths, \(\sqrt{10}\) is between 3.162 and 3.163 because
3.1622 < (\(\sqrt{10}\))2 < 3.1632. The decimal expansion of \(\sqrt{10}\) is approximately 3.162….
\(\frac{28}{9}\) = \(\frac{27}{9}\) + \(\frac{1}{9}\)
= 3 + \(\frac{1}{9}\)
In the interval of tenths, we are looking for the integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{1}{9}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{10}{9}\) < m + 1
\(\frac{10}{9}\) = \(\frac{9}{9}\) + \(\frac{1}{9}\)
= 1 + \(\frac{1}{9}\)
The tenths digit is 1. Since the fraction \(\frac{1}{9}\) has reappeared, we can assume that the next digit is also 1, and the work will continue to repeat. Therefore, the decimal expansion of \(\frac{28}{9}\)9 is 3.1111….
Therefore, \(\frac{28}{9}\) < \(\sqrt{10}\).
Alternatively: (\(\sqrt{10}\))2 = 10 and (\(\frac{28}{9}\))2 = 784/81, which is less than \(\frac{810}{81}\) or 10. Thus, \(\frac{28}{9}\) is the smaller number.
Question 5.
Sam says that \(\frac{7}{11}\) = 0.63, and Jaylen says that \(\frac{7}{11}\) = 0.636. Who is correct? Why?
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{7}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{70}{11}\) < \(\frac{m + 1}{10}\)
\(\frac{70}{11}\) = \(\frac{66}{11}\) + \(\frac{4}{11}\)
= 6 + \(\frac{4}{11}\)
The tenths digit is 6. The difference between \(\frac{7}{11}\) and \(\frac{6}{10}\) is
\(\frac{7}{11}\) – \(\frac{6}{10}\) = \(\frac{4}{110}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{4}{110}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{40}{11}\) < m + 1
\(\frac{40}{11}\) = \(\frac{33}{11}\) + \(\frac{7}{11}\)
= 3 + \(\frac{7}{11}\)
The hundredths digit is 3. Again, we see the fraction \(\frac{7}{11}\), which means the next decimal digit will be 6, as it was in the tenths place. This means we will again see the fraction \(\frac{4}{11}\), meaning we will have another digit of 3. Therefore, the decimal expansion of \(\frac{7}{11}\) is 0.6363….
Technically, Sam and Jaylen are incorrect because the fraction \(\frac{7}{11}\) is an infinite decimal. However, Sam is correct to the first two decimal digits of the number, and Jaylen is correct to the first three decimal digits of the number.
Eureka Math Grade 8 Module 7 Lesson 12 Exit Ticket Answer Key
Question 1.
Find the decimal expansion of \(\frac{41}{6}\) without using long division.
Answer:
\(\frac{41}{6}\) = \(\frac{36}{6}\) + \(\frac{5}{6}\)
= 6 + \(\frac{5}{6}\)
The ones digit is 6.
To determine in which interval of tenths the fraction lies, we look for integers m and m + 1 so that

The tenths digit is 8.
To determine in which interval of hundredths the fraction lies, we look for integers m and m + 1 so that

We are a third over a whole number of tenths and a third over a whole number of hundredths. We suspect we are in a repeating pattern and that \(\frac{41}{6}\) = 6.83333….
To check:
x = 6.8333…
10x = 68.3333…
10x = 68 + 0.3333…
10x = 68 + \(\frac{1}{3}\)
10x = \(\frac{204}{3}\) + \(\frac{1}{3}\)
10x = \(\frac{205}{3}\)
x = \(\frac{205}{30}\)
x = \(\frac{41}{6}\)
We are correct.
Eureka Math Grade 8 Module 7 Lesson 12 Area and Volume I Answer Key
Question 1.
Find the area of the square shown below.
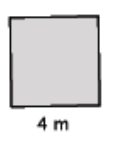
Answer:
A = (4 m)2
= 16 m2
Question 2.
Find the volume of the cube shown below.
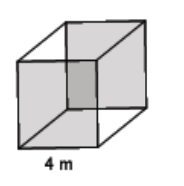
Answer:
V = (4 m)3
= 64 m3
Question 3.
Find the area of the rectangle shown below.
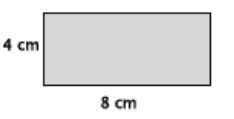
Answer:
A = (8 cm)(4 cm)
= 32 cm2
Question 4.
Find the volume of the rectangular prism shown below.
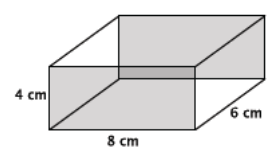
Answer:
V = (32 cm2)(6 cm)
= 192 cm3
Question 5.
Find the area of the circle shown below.
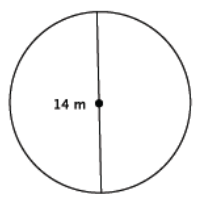
Answer:
A = (7 m)2 π
= 49π m2
Question 6.
Find the volume of the cylinder shown below.
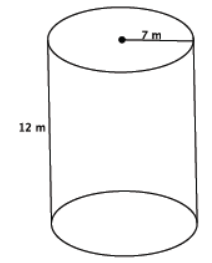
Answer:
V = (49π m2)(12 m)
= 588π m3
Question 7.
Find the area of the circle shown below.
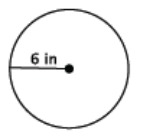
Answer:
A = (6 in.)2 π
= 36π in2
Question 8.
Find the volume of the cone shown below.
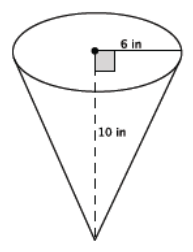
Answer:
V = (\(\frac{1}{3}\))(36π in2 )(10 in.)
= 120π in3
Question 9.
Find the area of the circle shown below.
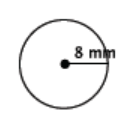
Answer:
A = (8 mm)2 π
= 64π mm2
Question 10.
Find the volume of the sphere shown below.
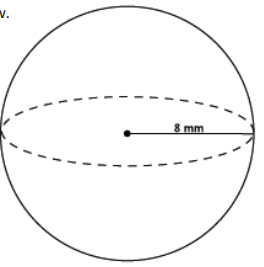
Answer:
V = (\(\frac{4}{3}\))π(64 mm2 )(8 mm)
= \(\frac{2048}{2}\) π mm3