Engage NY Eureka Math Grade 6 Module 5 Lesson 19a Answer Key
Eureka Math Grade 6 Module 5 Lesson 19a Opening Exercise Answer Key
Opening Exercise:
Question 1.
Determine the volume of this aquarium.
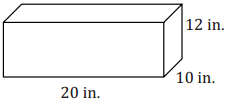
Answer:
V = l × w × h
V = 20 in. × 10 in. × 12 in.
V = 2,400 in3
Eureka Math Grade 6 Module 5 Lesson 19a Mathematical Modeling Exercise Answer Key
Mathematical Modeling Exercise: Using Ratios and Unit Rate to Determine Volume
For his environmental science project, Jamie is creating habitats for various wildlife including fish, aquatic turtles, and aquatic frogs. For each of these habitats, he uses a standard aquarium with length, width, and height dimensions measured in inches, identical to the aquarium mentioned in the Opening Exercise. To begin his project, Jamie needs to determine the volume, or cubic inches, of water that can fill the aquarium.
Use the table below to determine the unit rate of gallons/cubic inches.
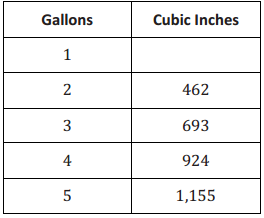
Answer:
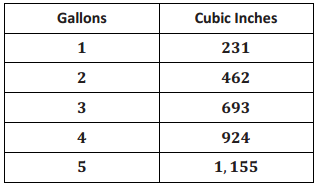
There are 231 cubic inches for every 1 gallon of water. So, the unit rate is 231.
→ Since we determined that for every gallon of water, there are 231 cubic inches, determine how many cubic inches are in the 10 gallons of water that Jamie needs for the fish.
→ How can we determine how many cubic inches are in 10 gallons of water?
We could use a tape diagram or a double number line, or we could find equivalent ratios.
→ Using either of these representations, determine the volume of the aquarium.
Determine the volume of this aquarium.
Answer:
Answers will vary depending on student choice. An example of a tape diagram is below.
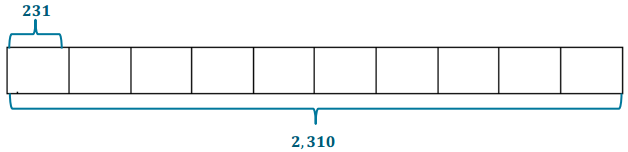
→ We determined the volume of this tank is 2,310 in3. This is not the same volume we calculated earlier in the Opening Exercise. Why do you think the volumes are different?
Answers will vary but should include a discussion that there needs to be room for a lid; also, the water level cannot go all the way to the top so that there is room for heaters, filters, and fish, etc., without the water spilling over.
→ Generally, it is suggested that the highest level of water in this tank should be approximately 11.55 inches.
Calculate the volume of the aquarium using this new dimension.
V = l × w × h; V = 20 in. × 10 in. × 11.55 in.; V = 2,310 in3
→ What do you notice about this volume?
This volume is the same as the volume we determined when we found the volume using ratio and unit rates.
→ Let’s use the dimensions 20 in. × 10 in. × 11.55 in. for our exploration.
Eureka Math Grade 6 Module 5 Lesson 19a Exercise Answer Key
Optional Exercise 1:
→ We have determined that the volume for the 10-gallon aquarium with dimensions 20 in. × 10 in. × 11.55 in.
is 2,310 in3.
→ Suppose Jamie needs to fill the aquarium to the top in order to prepare the tank for fish. According to our calculations, if Jamie pours 10 gallons of water into the tank, the height of the water is approximately 11.55 in.
→ Let’s test it. Begin pouring water into the aquarium 1 gallon at a time. Be sure to keep track of the number of gallons. Use a tally system.


→ Measure the height of the water with your ruler.
→ What did you find about our height calculation?
Our calculation was correct. The height is approximately 11.55 in.
Exercise 1:
a. Determine the volume of the tank when filled with 7 gallons of water.
Answer:
231 \(\frac{\text { cubic inches }}{\text { gallon }}\) = 1,617 in3
The volume for 7 gallons of water is 1,617 in3.
b. Work with your group to determine the height of the water when Jamie places 7 gallons of water in the aquarium.
Answer:
1,617 in3 = (20 in. )(10 in. ) h
\(\frac{1,617 \mathrm{in}^{3}}{200 \mathrm{in}^{2}}=\frac{200 \mathrm{in}^{2}}{200 \mathrm{in}^{2}} h\)
8.085 in. = h
The tank should have a water height of 8.085 inches.
Optional Exercise 2:
→ Let’s test it. Begin by pouring water into the aquarium 1 gallon at a time.
→ Be sure to keep track of the number of gallons poured. Use a tally system.
Or, have students mark the height of the water using a wax marker or a dry erase marker on the outside of the tank after each gallon is poured in. Then, students measure the intervals (distance between the marks). Students should notice that the intervals are equal.
→ Test the height at 7 gallons, and record the height measurement.

→ What did you find about our calculation?
Our calculation was correct. The height is about 8 inches.
Exercise 2:
a. Use the table from Example 1 to determine the volume of the aquarium when Jamie pours 3 gallons of water into the tank.
Answer:
The volume of the tank is 231 in3 × 3 = 693 in3.
b. Use the volume formula to determine the missing height dimension.
693 in3 = 20 in.(10 in.) h
\(\frac{693 \mathrm{in}^{3}}{200 \mathrm{in}^{2}}=\frac{200 \mathrm{in}^{2}}{200 \mathrm{in}^{2}} h\)
3.465 in. = h
The tank should have a water height of 3.465 in.
Optional Exercise 3:
→ Let’s test it. Begin by pouring water into the aquarium 1 gallon at a time.
→ Be sure to keep track of the number of gallons poured. Use a tally system.
→ Test the height at 3 gallons, and record the height measurement.

→ What did you find about our calculation?
Our calculation was correct. The height is about 3\(\frac{1}{2}\) inches.
Exercise 3:
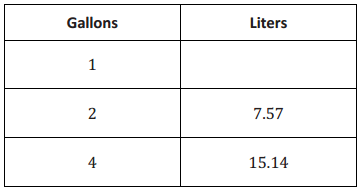
a. Using the table of values below, determine the unit rate of liters to gallon.
Answer:
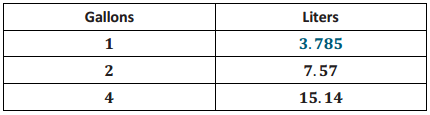
The unit rate is 3.785.
b. Using this conversion, determine the number of liters needed to fill the 10-gallon tank. liters.
Answer:
3.785 \(\frac{\text { liters }}{\text { gallon }}\) × 10 gallons = 37.85 liters
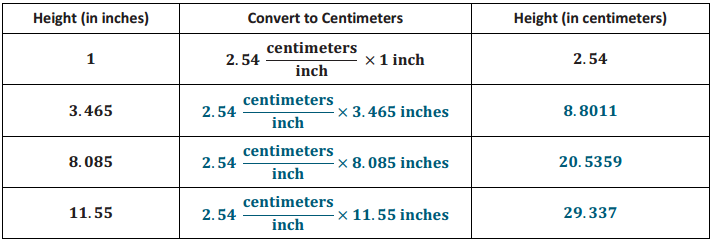
c. The ratio of the number of centimeters to the number of inches is 2.54: 1. What is the unit rate?
Answer:
2.54
d. Using this information, complete the table to convert the heights of the water in inches to the heights of the water in centimeters Jamie will need for his project at home.
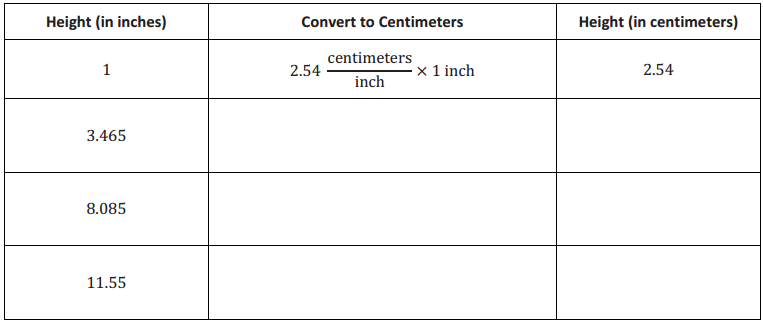
Answer:
Exercise 4:
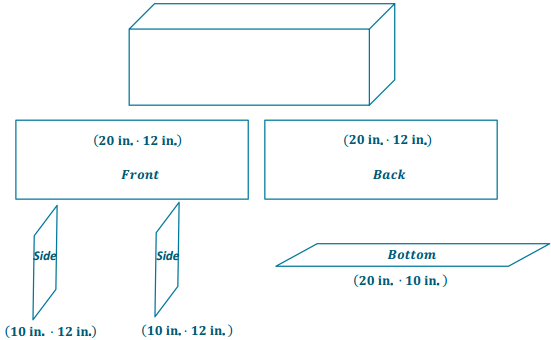
a. Determine the amount of plastic film the manufacturer uses to cover the aquarium faces. Draw a sketch of the aquarium to assist in your calculations. Remember that the actual height of the aquarium is inches.
Answer:
SA = (2lW) + (2lh) + (2wh)
SA = (2.20 in. . 10 in.) + (2.20 in. . 12 in.) + (2.10in. . 12 in.)
SA = 400 in2 + 480 in2 + 240 in2
SA = 1,120 in2
b. We do not include the measurement of the top of the aquarium since It is open without glass and does not need to be covered with film. Determine the area of the top of the aquarium, and find the amount of film the manufacturer uses to cover only the sides, front, back, and bottom.
Answer:
Area of the top of the aquarium = l . w
Area of the top of the aquarium = 20 in. . 10 in.
Area of the top of the aquarium = 200 in2
SA of aquarium without the top = 1,120 in2 – 200 in2 = 920 in2
c. Since Jamie needs three aquariums, determine the total surface area of the three aquariums.
Answer:
920 in2 + 920 in2 + 920 in2 = 2.760 in2 or 3920 in2 = 2,760 in2
Eureka Math Grade 6 Module 5 Lesson 19a Problem Set Answer Key
This Problem Set is a culmination of skills learned in this module. Note that the figures are not drawn to scale.
Question 1.
Calculate the area of the figure below.

Answer:
A = bh
A = (40 ft.) (20 ft.)
A = 800 ft2
Question 2.
Calculate the area of the figure below.
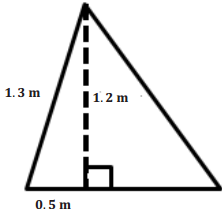
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1.3 m) (1.2 m)
A = 0.78 m2
Question 3.
Calculate the area of the figure below.
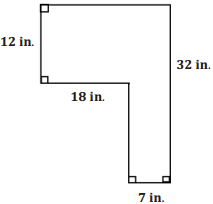
Answer:
Area of top rectangle:
A = lw
A = (25 in.)(12 in.)
A = 300 in2
Area of bottom rectangle:
A = lw
A= (7 in.)(20 in.)
A = 140 in2
Total Area = 300 in2 + 140 in2 = 440 in2
Question 4.
Complete the table using the diagram on the coordinate plane.

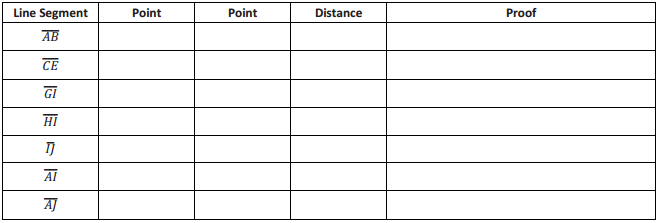
Answer:
Question 5.
Plot the points below, and draw the shape. Then, determine the area of the polygon. A(-3, 5), B(4, 3), C(0, -5)
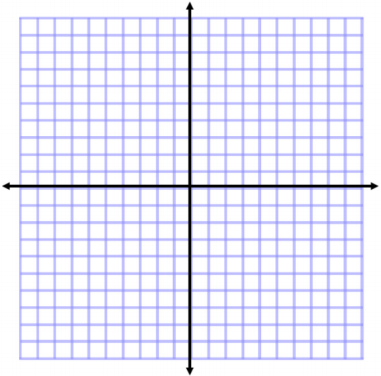
Answer:
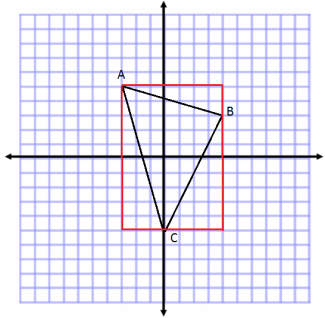
Area of Rectangle:
Area = lw
Area = (7 units)(10 units)
Area = 70 units2
Area of Triangle on Left:
Area = \(\frac{1}{2}\)bh
Area = \(\frac{1}{2}\)(3 units)(10 units)
Area = 15 units2
Area of Triangle on Top:
Area on top = \(\frac{1}{2}\)bh
Area = \(\frac{1}{2}\)(7 units) (2 units)
Area = 7 units2
Area of Triangle on Right:
Area = \(\frac{1}{2}\)bh
Area = \(\frac{1}{2}\)(4 units)(8 units)
Area = 16 units2
Total Area = 70 units2 – 15 units2 – 7 units2 – 16 units2
Total Area = 32 units2
Question 6.
Determine the volume of the figure.
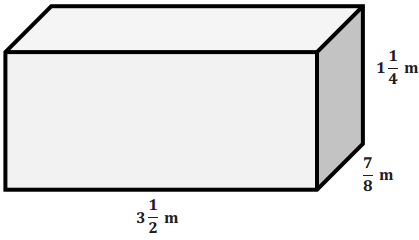
Answer:
V = l w h
V = (3\(\frac{1}{2}\) m) (\(\frac{7}{8}\) m) (1\(\frac{1}{4}\) m)
V = \(\frac{245}{64}\) m3
V = 3\(\frac{53}{64}\) m3
Question 7.
Give at least three more expressions that could be used to determine the volume of the figure in Problem 6.
Answer:
Answers will vary. Some examples include the following:
(\(\frac{35}{32}\) m2) (3\(\frac{53}{64}\) m)
(1\(\frac{1}{4}\) m) (\(\frac{7}{8}\) m) (3\(\frac{1}{2}\) m)
(\(\frac{49}{16}\) m2) (1\(\frac{1}{4}\) m)
Question 8.
Determine the volume of the irregular figure.
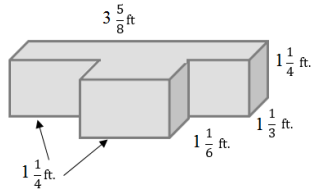
Answer:
Volume of the back Rectangular Prism:
V = l w h
V = (3\(\frac{5}{8}\) ft.) (1\(\frac{1}{3}\) ft) (1\(\frac{1}{4}\) ft.)
V = \(\frac{580}{96}\) ft3
Volume of the front Rectan guiar Prism:
V = l w h
V = (1\(\frac{1}{4}\) ft.) (1\(\frac{1}{6}\) ft.)(1\(\frac{1}{4}\) ft.)
V = \(\frac{175}{96}\) ft3
Total Volume = \(\frac{580}{96}\) ft3 + \(\frac{175}{96}\) ft3
= \(\frac{755}{96}\) ft3 = 7\(\frac{83}{96}\) ft3
Question 9.
Draw and label a net for the following figure. Then, use the net to determine the surface area of the figure.
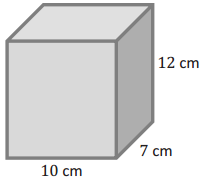
Answer:
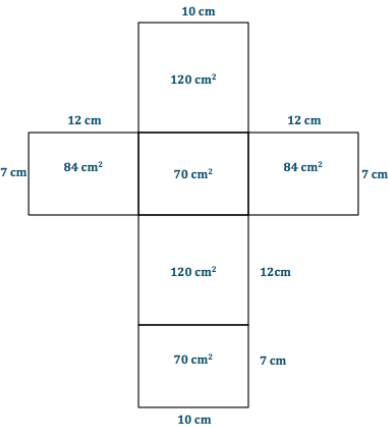
SA = 120 cm2 + 84 cm2 + 70 cm2 + 84 cm2 + 120 cm2 + 70 cm2
= 548 cm2
Question 10.
Determine the surface area of the figure in Problem 9 using the formula SA = 21w + 21h + 2wh. Then, compare your answer to the solution in Problem 9.
Answer:
SA = 2lw + 2lh + 2wh
SA = 2(10 cm)(7 cm) + 2(10 cm)(12 cm) + 2 (7 cm)(12 cm)
SA = 140 cm2 + 240 cm2 + 168 cm2
SA= 548 cm2
The answer in Problem 10 is the same as in Problem 9. The formula finds the areas of each pair of equal faces and adds them together, like we did with the net.
Question 11.
A parallelogram has a base of 4.5 cm and an area of 9.495 cm2. Tania wrote the equation 4.5x = 9.495 to represent this situation.
a. Explain what x represents in the equation.
Answer:
x represents the height of the parallelogram in centimeters.
b. Solve the equation for x and determine the height of the parallelogram.
Answer:
\(\frac{4.5 x}{4.5}=\frac{9.495}{4.5}\)
x = 2.11
The height of the parallelogram is 2.11 cm.
Question 12.
Triangle A has an area equal to one-third the area of Triangle B. Triangle A has an area of 3\(\frac{1}{2}\) square meters.
a. Gerard wrote the equation \(\frac{B}{3}\) = 3\(\frac{1}{2}\). Explain what B represents in the equation.
Answer:
B represents the area of Triangle B in square meters.
b. Determine the area of Triangle B.
Answer:
\(\frac{B}{3}\) . 3 = 3\(\frac{1}{2}\) . 3
The area of Triangle is 10\(\frac{1}{2}\) square meters.
Eureka Math Grade 6 Module 5 Lesson 19a Exit Ticket Answer Key
Question 1.
What did you learn today? Describe at least one situation in real life that would draw on the skills you used today.
Answer:
Answers will vary.