Eureka Math Geometry Module 5 Mid Module Assessment Answer Key

Engage NY Eureka Math Geometry Module 5 Mid Module Assessment Answer Key

Eureka Math Geometry Module 5 Mid Module Assessment Task Answer Key

Question 1.
Consider a right triangle drawn on a page with sides of lengths 3 cm, 4 cm, and 5 cm.

a. Describe a sequence of straightedge and compass constructions that allow you to draw the circle that circumscribes the triangle. Explain why your construction steps successfully accomplish this task.
Answer:

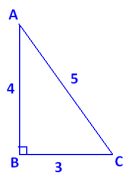
Label the vertices of the right triangle A , B , and C as shown. Because ∠ABC is a right angle, \(\overline{A C}\) will be the diameter of the circle. So, the midpoint of \(\overline{A C}\) is the center. We first need to construct that midpoint.
1. Set a compass at point A with its width equal to AC. Draw a circle.
2. Set the compass at point C with the same width AC. Draw a circle.
3. Connect the two points of intersection of these circles with a line segment. This line segment intersects \(\overline{A C}\) at its midpoint. Call it M.
4. Set the compass at point M with width MA. Draw the circle. This is the circumscribing circle for the triangle.
(Note that we could also locate the center of the circumscribing circle by constructing the perpendicular bisectors of any two sides of the triangle. Their point of intersection is the center.)

b. What is the distance of the side of the right triangle of length 3 cm from the center of the circle that circumscribes the triangle?
Answer:

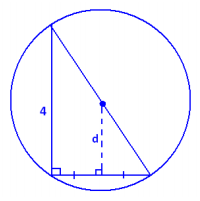
The distance, d, we seek is the length of the line segment connecting the center of the circumscribing circle to the midpoint of the side of the triangle of length 3 cm. This segment is perpendicular to that side. Thus, we see two similar right triangles with scale factor 2. It follows that
d = \(\frac{1}{2}\) ⋅ 4 = 2 , and the distance is 2 cm.

c. What is the area of the inscribed circle for the triangle?
Answer:

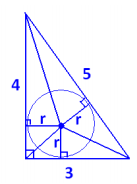
Draw in three radii for the inscribed circle, as shown. They meet the sides of the triangle at right angles. Each radius can be thought of as the height of a small triangle within the larger 3 – 4 – 5 triangle. If the radius of the inscribed circle is r, then the area of the whole 3-4-5 triangle is calculated as follows:
(\(\frac{1}{2}\) ⋅ 3 ⋅ r )+ (\(\frac{1}{2}\) ⋅ 4 ⋅ r )+ (\(\frac{1}{2}\) ⋅ 5 ⋅ r ) = 6r .
We know the area of the triangle is A= \(\frac{1}{2}\) ⋅ 3 ⋅ 4 = 6 , so we can conclude r = 1 . The radius of the inscribed circle is 1 cm; therefore, the area of the inscribed circle is A = π (1 cm)² = π cm².

Question 2.
A five-pointed star with vertices A, M, B, N, and C is inscribed in a circle as shown. Chords \(\overline{A B}\) and \(\overline{M C}\) intersect at point P.

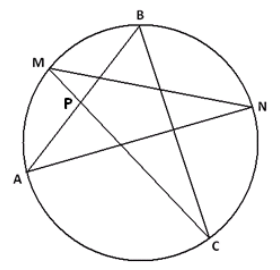
a. What is the value of m∠BAN + m∠NMC + m∠CBA + m∠ANM + m∠MCB, the sum of the measures of the angles in the points of the star? Explain your answer.
Answer:
The measure of ∠BAN is half the measure of the arc BN; the same is true for the four remaining angles. Thus, the sum of all five angle measures is half the sum of the measures of ALL the arcs in the circle.
Thus, the sum of all five angle measures is half the sum of the measures of all the arcs in the circle (360°). Thus, the sum of the measures of the angles is 180º.

b. Suppose M is the midpoint of the arc AB, N is the midpoint of arc BC, and m∠BAN = \(\frac{1}{2}\) m∠CBA. What is m∠BPC, and why?
Answer:

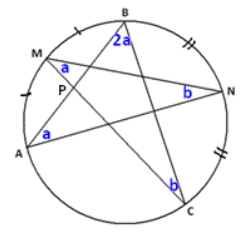
The angles marked a are congruent because they are inscribed angles from congruent arcs. This is similar for the angles marked b. We are also told that m∠CBA is double m∠BAN .

From part (a), we have 4a + 2b = 180° , so 2a + b = 90° .

Using the fact that angles in △BPC add to 180°, we get
m∠BPC = 180° – 2a – b = 90° .

Question 3.
Two chords, \(\overline{A C}\) and \(\overline{B D}\) in a circle with center O, intersect at right angles at point P. \(\overline{A B}\) is equal to the length of the radius of the circle.

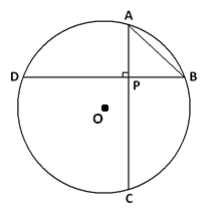
a. What is the measure of the arc AB?
Answer:

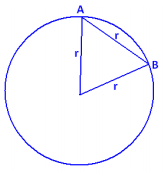
Draw in the central angle to chord \(\overline{A B}\). We see an equilateral triangle. The central angle, and hence arc AB, has measure 60°.

b. What is the value of the ratio \(\frac{DC}{AB}\)? Explain how you arrived at your answer.
Answer:

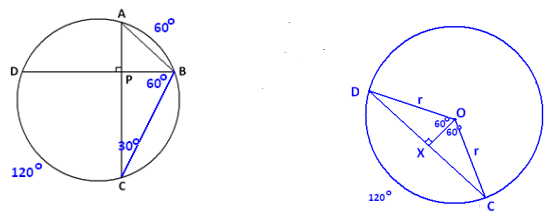
Draw chord \(\overline{B C}\). By the inscribed angle theorem, m∠ACB = 30° . In △PBC , it then follows that m∠PBC = 60° , so arc DC has a measure of 120°. Draw this central angle.
Draw \(\overline{O X}\) perpendicular to \(\overline{D C}\), as shown.
We see that △DXO is a 30 – 60 – 90 triangle, so OX = \(\frac{r}{2}\) .

Thus, DX=\(\sqrt{r^{2}-\left(\frac{r}{2}\right)^{2}}\)=\(\frac{\sqrt{3} r}{2}\), and DC = \(\sqrt{3}\)r , so \(\frac{DC}{AB}\) =\(\sqrt{3}\).

Question 4.
a. An arc of a circle has length equal to the diameter of the circle. What is the measure of that arc in radians? Explain your answer.
Answer:
An arc of length one radius of the circle represents one radian of turning. Thus, an arc of length two radii, a diameter, has a measure of 2 radians.

b. Two circles have a common center O. Two rays from O intercept the circles at points A, B, C, and D as shown.
Suppose OA : OB = 2 : 5 and that the area of the sector given by A, O, and D is 10 cm².

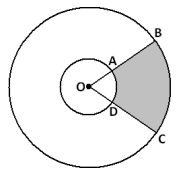
i. What is the ratio of the measure of the arc AD to the measure of the arc BC?
Answer:
Both arcs represent the same amount of turning (i.e., they have the same central angle), so they have the same measure. This ratio is 1.

ii. What is the area of the shaded region given by the points A, B, C, and D?
Answer:
Let θ be the measure of ∠AOD in radians. Since OA : OB = 2 : 5, we have that
OA = 2x, and OB = 5x for some value x.
To find the area of sector AOD: 10 cm ² = \(\frac{\theta}{2 \pi}\) ⋅ π (2x )² = 2θ x² , so θ x² = 5 cm² .
To find the area of sector BOC: \(\frac{\theta}{2 \pi}\) -π (5x)² = \(\frac{25}{2}\) θ x² = \(\frac{25}{2}\) (5 cm² )= \(\frac{125}{2}\) cm².
To find the area of the shaded region: \(\frac{125}{2}\) cm² – 10 cm² = 52.5 cm².
(Alternatively, the sectors AOD and BOC are similar with scale factor \(\frac{5}{2}\).
Thus, to find the area of sector BOC: 10 (\(\frac{5}{2}\))² = 12\(\frac{5}{2}\).
To find the area of the shaded region: \(\frac{125}{2}\) – 10 = 52.5 .
Therefore, the area of the shaded region is 52.5 cm².

iii. What is the ratio of the length of the arc AD to the length of the arc BC?
Answer:
Since the radii of the circles come in a 2 to 5 ratio, the same is true for these arc lengths.

Question 5.
In this diagram, the points P, Q, and R are collinear and are the centers of three congruent circles. Q is the point of contact of two circles that are externally tangent. The remaining points at which two circles intersect are labeled A, B, C, and D, as shown.

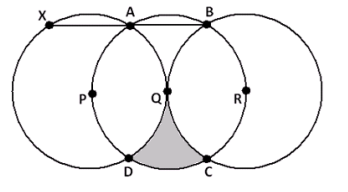
a. \(\overline{A B}\) is extended until it meets the circle with center P at a point X. Explain, in detail, why X, P, and D are collinear.
Answer:

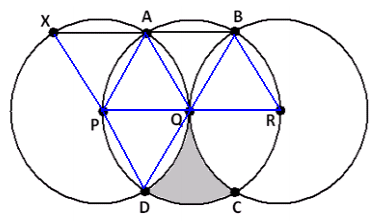
Draw in the radii shown.
Triangles APQ , QBR , and PQD are equilateral, so all angles in those triangles have measure 60° . △ABQ is isosceles with an angle at Q of measure 180° – 60° – 60° , or 60° . It follows that it is equilateral as well.
We have m∠XAP = 180° – m∠PAQ – m∠QAB = 180° – 60° – 60° = 60° . Since △XPA is isosceles, with one angle of measure 60°, it follows that it is also equilateral. In particular, m∠XPA = 60° .
Thus, m∠XPD = 60° + 60° + 60° = 180° , showing that X, P, and D are collinear.

b. In the diagram, a section is shaded. What percent of the full area of the circle with center Q is shaded?
Answer:
Draw the \(\overline{A D}\) shown. We see that it divides a sector of the circle with center Q into two regions, which we have labeled I and II.

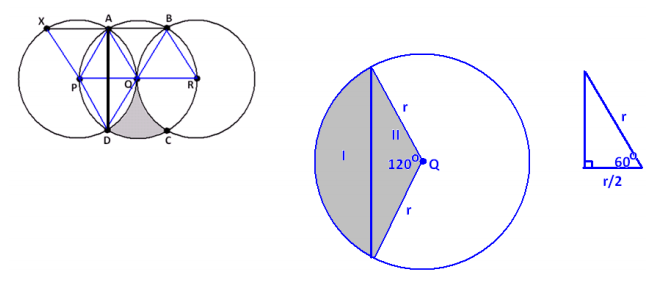
If we can determine the area of region I, then we see that the area of the desired shaded region is \(\frac{1}{2}\) (area full circle – 4 × area (region I )).
Now area (I + II ) = \(\frac{120}{360}\) πr ² = \(\frac{1}{3}\) πr ² , where r is the radius of the circle.
Region II is composed of two congruent right triangles, each containing a 60° angle and each with hypotenuse r. It follows that the remaining sides of each are \(\frac{r}{2}\) and \(\sqrt{r^{2}-\left(\frac{r}{2}\right)^{2}}\) = \(\frac{\sqrt{3} r}{2}\) . Thus, region II is a triangle with base \(\sqrt{3} r\) and height \(\frac{r}{2}\) , so it has an area of \(\frac{1}{2}\) × \(\sqrt{3} r\) × \(\frac{r}{2}\) = \(\frac{\sqrt{3}}{4}\)r . We have area I = area (I + II )-area II = \(\frac{1}{3}\) πr² – \(\frac{\sqrt{3}}{4}\) r ² .
Thus, the shaded region in question has an area of
\(\frac{1}{2}\) (πr ² – 4 (\(\frac{1}{3}\) πr² – \(\frac{\sqrt{3}}{4}\) r²)) = \(\frac{1}{2}\) πr ² – \(\frac{2}{3}\) πr² + \(\frac{\sqrt{3}}{2}\) r² = (\(\frac{\sqrt{3}}{2}-\frac{\pi}{6}\)) r ² .
To find the percentage of the full area of the circle:
\(\frac{\left(\frac{\sqrt{3}}{2}-\frac{\pi}{6}\right) r^{2}}{\pi r^{2}}\) = \(\frac{\sqrt{3}}{2 \pi}\) – \(\frac{1}{6}\)
The shaded area is about 10.9% of the full area of the circle with center Q.