Engage NY Eureka Math Geometry Module 1 Lesson 23 Answer Key
Eureka Math Geometry Module 1 Lesson 23 Exploratory Challenge Answer Key
Exploratory Challenge
Today we examine a geometry fact that we already accept to be true. We are going to prove this known fact in two ways:
(1) by using transformations and
(2) by using SAS triangle congruence criteria.
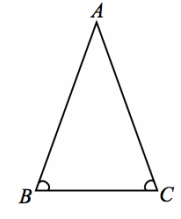
Here is isosceles triangle ABC. We accept that an isosceles triangle, which has (at least) two congruent sides, also has congruent base angles.
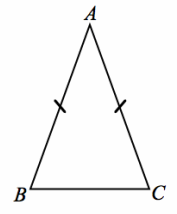
Label the congruent angles in the figure.
Now we prove that the base angles of an isosceles triangle are always congruent.
Prove Base Angles of an Isosceles are Congruent: Transformations
While simpler proofs do exist, this version is included to reinforce the idea of congruence as defined by rigid motions. Allow 15 minutes for the first proof.
Prove Base Angles of an Isosceles are Congruent: Transformations
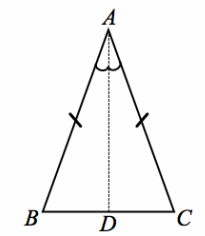
Given: Isosceles △ABC, with AB=AC
Prove: m∠B=m∠C
Construction: Draw the angle bisector \(\overrightarrow{A D}\) of ∠A, where D is the intersection of the bisector and \(\overline{B C}\). We need to show that rigid motions maps point B to point C and point C to point B.
Let r be the reflection through \(\overleftrightarrow{\boldsymbol{A D}}\). Through the reflection, we want to demonstrate two pieces of information that map B to point C and vice versa:
(1) \(\overrightarrow{A B}\) maps to \(\overrightarrow{A C}\), and
(2) AB=AC.
Since A is on the line of reflection, \(\overleftrightarrow{\boldsymbol{A D}}\), r(A)=A. Reflections preserve angle measures, so the measure of the reflected angle r(∠BAD) equals the measure of ∠CAD; therefore, r(\(\overrightarrow{A B}\))=(\(\overrightarrow{A C}\)). Reflections also preserve lengths of segments; therefore, the reflection of \(\overline{A B}\) still has the same length as \(\overline{A B}\). By hypothesis, AB=AC, so the length of the reflection is also equal to AC. Then r(B)=C. Using similar reasoning, we can show that r(C)=B.
Reflections map rays to rays, so r(\(\overrightarrow{B A}\))=(\(\overrightarrow{C A}\)) and r(\(\overrightarrow{B C}\))=\(\overrightarrow{C B}\). Again, since reflections preserve angle measures, the measure of r(∠ABC) is equal to the measure of ∠ACB.
We conclude that m∠B=m∠C. Equivalently, we can state that ∠B≅∠C. In proofs, we can state that “base angles of an isosceles triangle are equal in measure” or that “base angles of an isosceles triangle are congruent.”
Prove Base Angles of an Isosceles are Congruent: SAS
Allow 10 minutes for the second proof.
Prove Base Angles of an Isosceles are Congruent: SAS
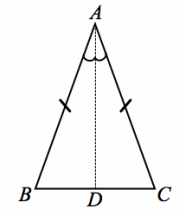
Given: Isosceles △ABC, with AB=AC
Prove: ∠B≅∠C
Construction: Draw the angle bisector \(\overrightarrow{A D}\) of ∠A, where D is the intersection of the bisector and \(\overline{B C}\). We are going to use this auxiliary line towards our SAS criteria.
Allow students five minutes to attempt the proof on their own.
Answer:
AB=AC Given
AD=AD Reflexive property
m∠BAD=m∠CAD Definition of an angle bisector
△ABD≅ △ACD SAS
∠B≅∠C Corresponding angles of congruent triangles are congruent.
Eureka Math Geometry Module 1 Lesson 23 Exercise Answer Key
Opening Exercise
Describe the additional piece of information needed for each pair of triangles to satisfy the SAS triangle congruence criteria.
a. Given: AB=DC
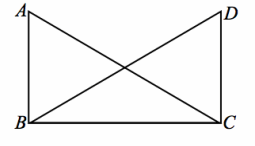
Answer:
\(\overline{A B}\) ⊥\(\overline{B C}\) , \(\overline{D C}\) ⊥\(\overline{C B}\) , or m∠B=m∠C
Prove: △ABC≅ △DCB
b. Given: AB=RS
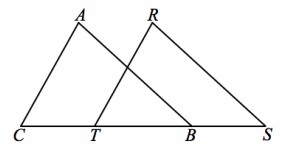
\(\overline{A B}\) ∥\(\overline{R S}\)
Answer:
CB=TS, or CT=BS
Prove: △ABC≅ △RST
Exercises
Exercise 1.
Given: JK=JL; \(\overline{J R}\) bisects \(\overline{K L}\)
Prove: \(\overline{J R}\) ⊥\(\overline{K L}\)
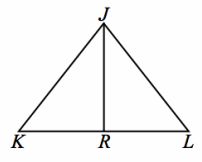
Answer:
JK=JL Given
∠K≅∠L Base angles of an isosceles triangle are congruent.
KR=RL Definition of a segment bisector
∴ △JRK≅ △JRL SAS
∠JRK≅∠JRL Corresponding angles of congruent triangles are congruent.
m∠JRK+m∠JRL=180° Linear pairs form supplementary angles.
2(m∠JRK)=180° Substitution property of equality
m∠JRK=90° Division property of equality
∴\(\overline{J R}\) ⊥\(\overline{K L}\) Definition of perpendicular lines
Exercise 2.
Given: AB=AC, XB=XC
Prove: \(\overline{A X}\) bisects ∠BAC
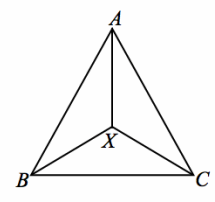
Answer:
AB=AC Given
m∠ABC=m∠ACB Base angles of an isosceles triangle are equal in measure.
XB=XC Given
m∠XBC=m∠XCB Base angles of an isosceles triangle are equal in measure.
m∠ABC=m∠ABX+m∠XBC,
m∠ACB=m∠ACX+m∠XCB Angle addition postulate
m∠ABX=m∠ABC-m∠XBC,
m∠ACX=m∠ACB-m∠XCB Subtraction property of equality
m∠ABX=m∠ACX Substitution property of equality
∴ △ABX≅ △ACX SAS
∠BAX≅∠CAX Corresponding parts of congruent triangles are congruent.
∴ \(\overline{A X}\) bisects ∠BAC. Definition of an angle bisector
Exercise 3.
Given: JX=JY, KX=LY
Prove: △JKL is isosceles
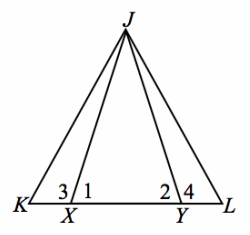
Answer:
JX=JY Given
KX=LY Given
m∠1=m∠2 Base angles of an isosceles triangle are equal in measure.
m∠1+m∠3=180° Linear pairs form supplementary angles.
m∠2+m∠4=180° Linear pairs form supplementary angles.
m∠3=180°-m∠1 Subtraction property of equality
m∠4=180°-m∠3 Subtraction property of equality
m∠3=m∠4 Substitution property of equality
∴ △JKX≅△JYL SAS
(JK) ̅≅(JL) ̅ Corresponding parts of congruent triangles are congruent.
∴ △JKL is isosceles. Definition of an isosceles triangle
Exercise 4.
Given: △ABC, with m∠CBA=m∠BCA
Prove: BA=CA
(Converse of base angles of isosceles triangle)
Hint: Use a transformation.
Answer:
PROOF:
We can prove that AB=AC by using rigid motions. Construct the perpendicular bisector l to \(\overline{B C}\). Note that we do not know whether the point A is on l. If we did, we would know immediately that AB=AC, since all points on the perpendicular bisector are equidistant from B and C. We need to show that A is on l, or equivalently, that the reflection across l takes A to A.
Let rl be the transformation that reflects the △ABC across l. Since l is the perpendicular bisector, rl(B)=C and rl(C)=B. We do not know where the transformation takes A; for now, let us say that rl(A)=A’.
Since ∠CBA≅∠BCA and rigid motions preserve angle measures, after applying rl to ∠BCA, we get that ∠CBA≅∠CBA’. ∠CBA and ∠CBA’ share a ray BC, are of equal measure, and A and A’ are both in the same half-plane with respect to line BC. Hence, \(\overrightarrow{\boldsymbol{B A}}\) and \(\overrightarrow{\boldsymbol{B A}^{\prime}}\) are the same ray. In particular, A’ is a point somewhere on \(\overrightarrow{\boldsymbol{B A}}\).
Likewise, applying rl to ∠CBA gives ∠BCA≅∠BCA’, and for the same reasons in the previous paragraph, A’ must also be a point somewhere on \(\overrightarrow{\boldsymbol{C A}}\). Therefore, A’ is common to both \(\overrightarrow{\boldsymbol{B A}}\) and \(\overrightarrow{C A}\).
The only point common to both \(\overrightarrow{\boldsymbol{B A}}\) and \(\overrightarrow{\boldsymbol{C A}}\) is point A; thus, A and A’ must be the same point, i.e., A=A’.
Hence, the reflection takes A to A, which means A is on the line l and rl(\(\overline{\boldsymbol{B} \boldsymbol{A}}\))= \(\overline{\boldsymbol{C} \boldsymbol{A’}}\)= \(\overline{\boldsymbol{C} \boldsymbol{A}}\), or BA=CA.
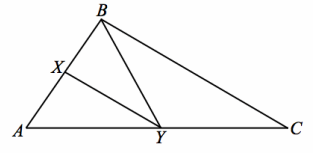
Exercise 5.
Given: △ABC, with \(\overline{X Y}\) is the angle bisector of ∠BYA, and \(\overline{B C}\) ∥ \(\overline{X Y}\)
Prove: YB=YC
Answer:
\(\overline{B C}\) || \(\overline{X Y}\) Given
m∠XYB=m∠CBY When two parallel lines are cut by a transversal, the alternate interior angles are equal.
m∠XYA=m∠BCY When two parallel lines are cut by a transversal, the corresponding angles are equal.
m∠XYA=m∠XYB Definition of an angle bisector
m∠CBY=m∠BCY Substitution property of equality
YB=YC When the base angles of a triangle are equal in measure, the triangle is isosceles.
Eureka Math Geometry Module 1 Lesson 23 Problem Set Answer Key
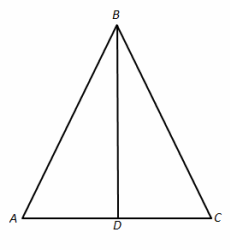
Question 1.
Given: AB=BC, AD=DC
Prove: △ADB and △CDB are right triangles
Answer:
AB=BC Given
△ABC is isosceles. Definition of isosceles triangle
m∠A=m∠C Base angles of an isosceles triangle are equal in measure.
AD=DC Given
△ADB≅ △CDB SAS
m∠ADB=m∠CDB Corresponding angles of congruent triangles are equal in measure.
m∠ADB+m∠CDB=180° Linear pairs form supplementary angles.
2(m∠ADB)=180° Substitution property of equality
m∠ADB=90° Division property of equality
m∠CDB=90° Transitive property
△ADB and △CDB are right triangles. Definition of a right triangle
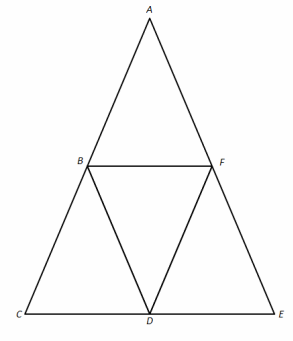
Question 2.
Given: AC=AE and \(\overline{B F}\) || \(\overline{C E}\)
Prove: AB=AF
Answer:
AC=AE Given
△ACE is isosceles. Definition of isosceles triangle
m∠ACE=m∠AEC Base angles of an isosceles triangle are equal in measure.
\(\overline{B F}\) || \(\overline{C E}\) Given
m∠ACE=m∠ABF If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
m∠AFB=m∠AEC If parallel lines are cut by a transversal, then corresponding angles are equal in measure.
m∠AFB=m∠ABF Transitive property
△ABF is isosceles. If the base angles of a triangle are equal in measure, the triangle is isosceles.
AB=AF Definition of an isosceles triangle
Question 3.
In the diagram, △ABC is isosceles with \(\overline{A C}\) ≅ \(\overline{A B}\). In your own words, describe how transformations and the properties of rigid motions can be used to show that ∠C≅∠B.
Answer:
Answers will vary. A possible response would summarize the key elements of the proof from the lesson, such as the response below.
It can be shown that ∠C≅∠B using a reflection across the bisector of ∠A. The two angles formed by the bisector of ∠A would be mapped onto one another since they share a ray, and rigid motions preserve angle measure.
Since segment length is also preserved, B is mapped onto C and vice versa.
Finally, since rays are taken to rays and rigid motions preserve angle measure, \(\overrightarrow{\boldsymbol{C A}}\) is mapped onto \(\overrightarrow{\boldsymbol{B A}}\), \(\overrightarrow{\boldsymbol{C B}}\) is mapped onto \(\overrightarrow{\boldsymbol{B C}}\), and ∠C is mapped onto ∠B. From this, we see that ∠C≅∠B.
Eureka Math Geometry Module 1 Lesson 23 Exit Ticket Answer Key
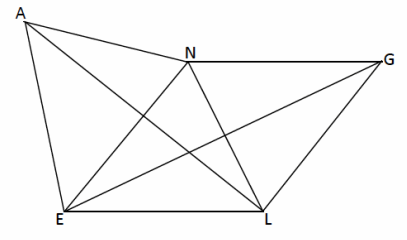
For each of the following, if the given congruence exists, name the isosceles triangle and the pair of congruent angles for the triangle based on the image above.
Question 1.
\(\overline{A E}\) ≅ \(\overline{L E}\)
Answer:
△AEL, ∠EAL≅∠ELA
Question 2.
\(\overline{L E}\) ≅\(\overline{L G}\)
Answer:
△LEG, ∠LEG≅∠LGE
Question 3.
\(\overline{A N}\) ≅\(\overline{L N}\)
Answer:
△NLA, ∠NLA≅∠NAL
Question 4.
\(\overline{E N}\) ≅\(\overline{G N}\)
Answer:
△NGE, ∠NGE≅∠NEG
Exercise 5.
\(\overline{N G}\) ≅\(\overline{L G}\)
Answer:
△GLN, ∠GNL≅∠GLN
Exercise 6.
\(\overline{A E}\) ≅\(\overline{N E}\)
Answer:
△AEN, ∠ENA≅∠EAN