Engage NY Eureka Math Geometry Module 5 Lesson 21 Answer Key
Eureka Math Geometry Module 5 Lesson 21 Exploratory Challenge Answer Key
Exploratory Challenge: A Journey to Ptolemy’s Theorem
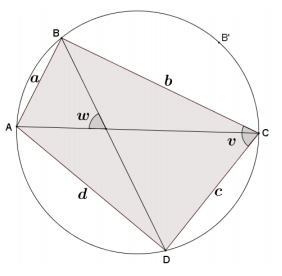
The diagram shows cyclic quadrilateral ABCD with diagonals \(\overline{A C}\) and \(\overline{B D}\) intersecting to form an acute angle with degree measure w.
AB = a, BC = b, CD = c, and DA = d.
a. From the last lesson, what is the area of quadrilateral ABCD in terms of the lengths of its diagonals and the angle w? Remember this formula for later.
Answer:
Area(ABCD) = \(\frac{1}{2}\) AC ⋅ BD ⋅ sinw
b. Explain why one of the angles, ∠BCD or ∠BAD, has a measure less than or equal to 90°.
Answer:
Opposite angles of a cyclic quadrilateral are supplementary. These two angles cannot both have measures greater than 90° (both angles could be equal to 90°).
c. Let’s assume that ∠BCD in our diagram is the angle with a measure less than or equal to 90°. Call its measure v degrees. What is the area of triangle BCD in terms of b, c, and v? What is the area of triangle BAD in terms of a, d, and v? What is the area of quadrilateral ABCD in terms of a, b, c, d, and v?
Answer:
If v represents the degree measure of an acute angle, then 180˚-v would be the degree measure of angle BAD since opposite angles of a cyclic quadrilateral are supplementary. The area of triangle BCD could then be calculated using \(\frac{1}{2}\) bc ⋅ sin(v), and the area of triangle BAD could be calculated by
\(\frac{1}{2}\) ad ⋅ sin(180˚ – (180˚ – v)), or \(\frac{1}{2}\) ad ⋅ sin(v). So, the area of the quadrilateral ABCD is the sum of the areas of triangles BAD and BCD, which provides the following:
Area(ABCD) = \(\frac{1}{2}\) ad ⋅ sinv + \(\frac{1}{2}\) bc ⋅ sinv .
d. We now have two different expressions representing the area of the same cyclic quadrilateral ABCD. Does it seem to you that we are close to a proof of Ptolemy’s claim?
Answer:
Equating the two expressions gives us a relationship that does, admittedly, use the four side lengths of the quadrilateral and the two diagonal lengths, but we also have terms that involve sin(w) and sin(v). These terms are not part of Ptolemy’s equation.
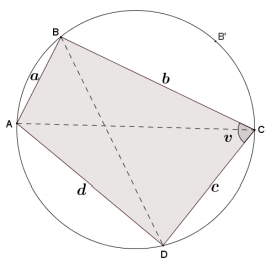
e. Trace the circle and points A, B, C, and D onto a sheet of patty paper. Reflect triangle ABC about the perpendicular bisector of diagonal \(\overline{A C}\). Let A’, B’, and C’ be the images of the points A, B, and C, respectively.
i. What does the reflection do with points A and C?
Answer:
Because the reflection was done about the perpendicular bisector of the diagonal (AC) ̅, the endpoints of the diagonal are images of each other (i.e., A = C’ and C = A’).
ii. Is it correct to draw B’ as on the circle? Explain why or why not.
Answer:
Reflections preserve angle measure. Thus, ∠AB’C ≅ ∠ABC. Also, ∠ABC is supplementary to ∠CDA; thus, ∠AB’C is too. This means that AB’CD is a quadrilateral with one pair (and, hence, both pairs) of opposite angles supplementary. Therefore, it is cyclic. This means that B’ lies on the circle that passes through A, C, and D. And this is the original circle.
iii. Explain why quadrilateral AB’CD has the same area as quadrilateral ABCD.
Answer:
Triangle AB’C is congruent to triangle ABC by a congruence transformation, so these triangles have the same area. It now follows that the two quadrilaterals have the same area.
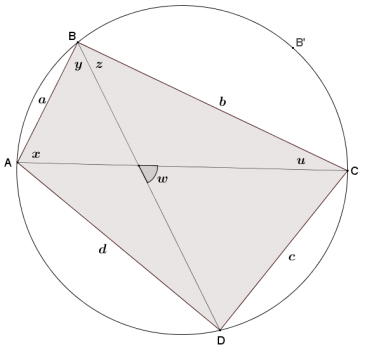
f. The diagram shows angles having degree measures u, w, x, y, and z.
Find and label any other angles having degree measures u, w, x, y, or z, and justify your answers.
Answer:
See diagram. Justifications include the inscribed angle theorem and vertical angles.
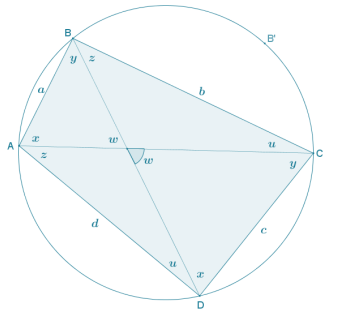
g. Explain why w = u + z in your diagram from part (f).
Answer:
The angle with degree measure w is an exterior angle to a triangle with two remote interior angles u and z. It follows that w = u + z.
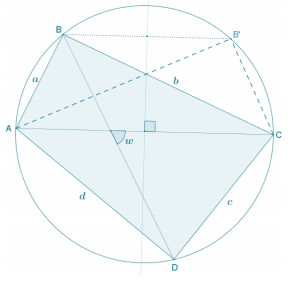
h. Identify angles of measures u, x, y, z, and w in your diagram of the cyclic quadrilateral AB’CD from part (e).
Answer:
See diagram below.
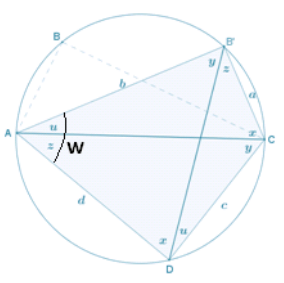
i. Write a formula for the area of triangle B’ AD in terms of b, d, and w. Write a formula for the area of triangle B’ CD in terms of a, c, and w.
Answer:
Area(B’ AD) = \(\frac{1}{2}\) bd ⋅ sin(w)
and
Area(B’ CD) = \(\frac{1}{2}\) ac ⋅ sin(w)
j. Based on the results of part (i), write a formula for the area of cyclic quadrilateral ABCD in terms of a, b, c, d, and w.
Answer:
Area(ABCD) = Area(AB’ CD) = \(\frac{1}{2}\) bd ⋅ sin(w) + \(\frac{1}{2}\) ac ⋅ sin(w)
k. Going back to part (a), now establish Ptolemy’s theorem.
Answer:
\(\frac{1}{2}\) AC ⋅ BD ⋅ sin(w) = \(\frac{1}{2}\) bd ⋅ sin(w) + \(\frac{1}{2}\) ac ⋅ sin(w)The two formulas represent the same area.
\(\frac{1}{2}\) ⋅ sin(w) ⋅ (AC ⋅ BD) = \(\frac{1}{2}\) ⋅ sin(w) ⋅ (bd + ac) Distributive property
AC ⋅ BD = bd + ac Multiplicative property of equality
or
AC ⋅ BD = (BC ⋅ AD) + (AB ⋅ CD) Substitution
Eureka Math Geometry Module 5 Lesson 21 Exercise Answer Key
Opening Exercise
Ptolemy’s theorem says that for a cyclic quadrilateral ABCD,
AC ⋅ BD = AB ⋅ CD + BC ⋅ AD.
With ruler and a compass, draw an example of a cyclic quadrilateral. Label its vertices A, B, C, and D.
Draw the two diagonals \(\overline{A C}\) and \(\overline{B D}\).
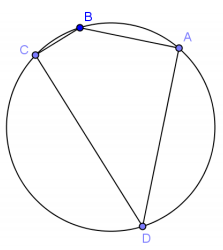
With a ruler, test whether or not the claim that AC ⋅ BD = AB ⋅ CD + BC ⋅ AD seems to hold true.
Repeat for a second example of a cyclic quadrilateral.
Challenge: Draw a cyclic quadrilateral with one side of length zero. What shape is this cyclic quadrilateral? Does Ptolemy’s claim hold true for it?
Answer:
Students will see that the relationship AC ⋅ BD = AB ⋅ CD + BC ⋅ AD seems to hold, within measuring error. For a quadrilateral with one side of length zero, the figure is a triangle inscribed in a circle. If the length AB = 0, then the points A and B coincide, and Ptolemy’s theorem states AC ⋅ AD = 0 ⋅ CD + AC ⋅ AD, which is true.
Eureka Math Geometry Module 5 Lesson 21 Problem Set Answer Key
Question 1.
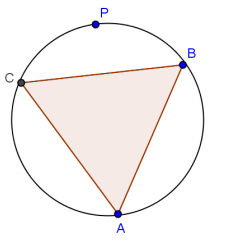
An equilateral triangle is inscribed in a circle. If P is a point on the circle, what does Ptolemy’s theorem have to say about the distances from this point to the three vertices of the triangle?
Answer:
It says that the sum of the two shorter distances is equal to the longer distance.
Question 2.
Kite ABCD is inscribed in a circle. The kite has an area of 108 sq.in., and the ratio of the lengths of the non-congruent adjacent sides is 3 : 1. What is the perimeter of the kite?
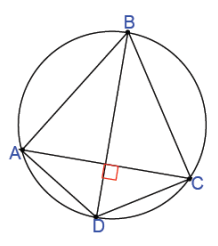
Answer:
\(\frac{1}{2}\) AC ⋅ BD = 108
AC ⋅ BD = AB ⋅ CD + BC ⋅ AD = 216
Since AB = BC and AD = CD, then
AC ⋅ BD = AB ⋅ CD + AB ⋅ CD
2(AB ⋅ CD) = 216
AB ⋅ CD = 108.
Let x be the length of \(\overline{C D}\), then
x ⋅ 3x = 108
3x2 = 108
x2 = 36
x = 6.
Therefore, CD and AD are 6 in. and AB and BC are 18 in., and the perimeter of kite ABCD is 48 in.
Question 3.
Draw a right triangle with leg lengths a and b and hypotenuse length c. Draw a rotated copy of the triangle such that the figures form a rectangle. What does Ptolemy have to say about this rectangle?
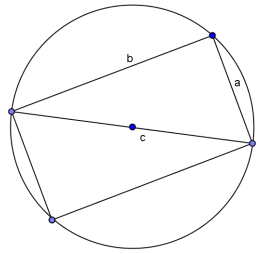
Answer:
We get a2 + b2 = c2, the Pythagorean theorem.
Question 4.
Draw a regular pentagon of side length 1 in a circle. Let b be the length of its diagonals. What does Ptolemy’s theorem say about the quadrilateral formed by four of the vertices of the pentagon?
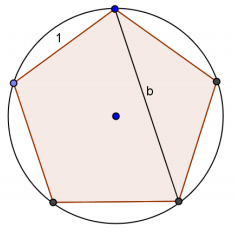
Answer:
b2 = b + 1, so b = \(\frac{\sqrt{5} + 1}{2}\). (This is the famous golden ratio!)
Question 5.
The area of the inscribed quadrilateral is \(\sqrt{300}\) mm2. Determine the circumference of the circle.
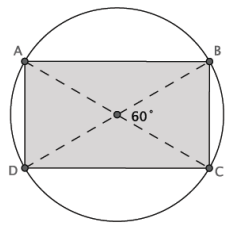
Answer:
Since ABCD is a rectangle, then AD ⋅ AB = \(\sqrt{300}\), and the diagonals are diameters of the circle.
The length of AB = 2r sin60, and the length of AD = 2r sin30, so \(\frac{AB}{AD}\) = \(\sqrt{3}\), and AB = \(\sqrt{3}\) (AD).
AD ⋅ \(\sqrt{3}\) (AD) = \(\sqrt{300}\)
AD2 = \(\frac{\sqrt{300}}{\sqrt{3}}\)
AD2 = 10
AD = \(\sqrt{10}\)
AB = \(\frac{\sqrt{30}}{\sqrt{3}}\)
AB ⋅ DC + AD ⋅ BC = AC ⋅ BD
(\(\sqrt{30}\) ⋅ \(\sqrt{30}\)) + (\(\sqrt{10}\) ⋅ \(\sqrt{10}\)) = AC ⋅ AC
30 + 10 = AC2
40 = AC2
2\(\sqrt{10}\) = AC
Since AC is 2\(\frac{\sqrt{10}}{\sqrt{3}}\) mm, the radius of the circle is \(\sqrt{10}\) mm, and the circumference of the circle is 2\(\frac{\sqrt{10}}{\sqrt{3}}\)π mm.
Question 6.
Extension: Suppose x and y are two acute angles, and the circle has a diameter of 1 unit. Find a, b, c, and d in terms of x and y. Apply Ptolemy’s theorem, and determine the exact value of sin(75).
Use scaffolded questions below as needed.
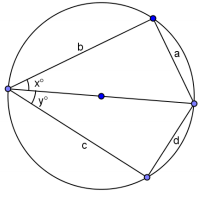
a. Explain why \(\frac{a}{sin(x)}\) equals the diameter of the circle.
Answer:
If the diameter is 1, this is a right triangle because it is inscribed in a semicircle, so sin(x) = \(\frac{a}{1}\), or 1 = \(\frac{a}{sin(x)}\). Since the diameter is 1, the diameter is equal to \(\frac{a}{sin(x)}\) .
b. If the circle has a diameter of 1, what is a?
Answer:
a = sin(x)
c. Use Thales’ theorem to write the side lengths in the original diagram in terms of x and y.
Answer:
Since both are right triangles, the side lengths are a = sin(x), b = cos(x), c = cos(y), and d = sin(y).
d. If one diagonal of the cyclic quadrilateral is 1, what is the other?
Answer:
sin(x + y)
e. What does Ptolemy’s theorem give?
Answer:
1 ∙ sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
f. Using the result from part (e), determine the exact value of sin(75).
Answer:
sin(75) = sin(30 + 45) = sin(30)cos(45) + cos(30)sin(45) = \(\frac{1}{2}\) ∙ \(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{3}}{2}\) ∙ \(\frac{\sqrt{2}}{2}\) = \(\frac{\sqrt{2} + \sqrt{6}}{4}\)
Eureka Math Geometry Module 5 Lesson 21 Exit Ticket Answer Key
Question 1.
What is the length of the chord \(\overline{A C}\)? Explain your answer.
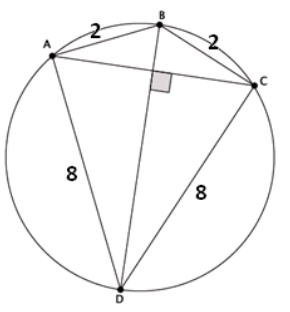
Answer:
Chord \(\overline{B D}\) is a diameter of the circle because it makes a right angle with chord AC, and BD = \(\sqrt{2^{2} + 8^{2}}\) = \(\sqrt{68}\).
By Ptolemy’s theorem: AC ∙ \(\sqrt{68}\) = 2 ∙ 8 + 2 ∙ 8, giving AC = \(\frac{16 \sqrt{17}}{17}\).