Engage NY Eureka Math Geometry Module 5 Lesson 20 Answer Key
Eureka Math Geometry Module 5 Lesson 20 Example Answer Key
Example
Given quadrilateral ABCD with m∠A + m∠C = 180°, prove that quadrilateral ABCD is cyclic; in other words, prove that points A, B, C, and D lie on the same circle.
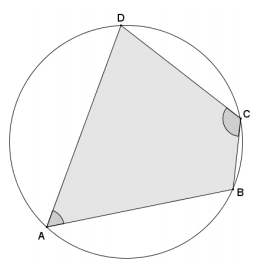
Answer:
→ First, we are given that angles A and C are supplementary. What does this mean about angles B and D, and why?
The angle sum of a quadrilateral is 360°, and since it is given that angles A and C are supplementary, angles B and D must then have a sum of 180°.
→ We, of course, can draw a circle through point A, and we can further draw a circle through points A and B (infinitely many circles, actually). Can we draw a circle through points A, B, and C?
→ Three non – collinear points can determine a circle, and since the points were given to be vertices of a quadrilateral, the points are non – collinear, so yes.
→ Can we draw a circle through points A, B, C, and D?
Not all quadrilaterals are cyclic (e.g., a non – rectangular parallelogram), so we cannot assume that a circle can be drawn through vertices A, B, C, and D.
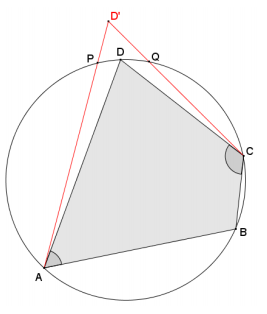
→ Where could point D lie in relation to the circle?
D could lie on the circle, in the interior of the circle, or on the exterior of the circle.
To show that D lies on the circle with A, B, and C, we need to consider the cases where it is not, and show that those cases are impossible. First, let’s consider the case where D is outside the circle. On the diagram, use a red pencil to locate and label point D’ such that it is outside the circle; then, draw segments CD’ and AD’.
→ What do you notice about sides \(\overline{A D^{\prime}}\) and \(\overline{C D^{\prime}}\) if vertex D’ is outside the circle?
The sides intersect the circle and are, therefore, secants.

Eureka Math Geometry Module 5 Lesson 20 Exercise Answer Key
Opening Exercise
Given cyclic quadrilateral ABCD shown in the diagram, prove that x + y = 180°.
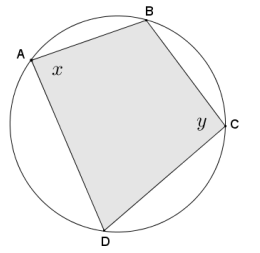
Answer:

Exercises
Exercise 1.
Assume that vertex D” lies inside the circle as shown in the diagram. Use a similar argument to the Example to show that vertex D” cannot lie inside the circle.
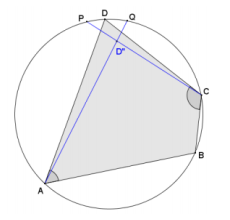
Answer:

Exercise 2.
Quadrilateral PQRS is a cyclic quadrilateral. Explain why △PQT ~△SRT.
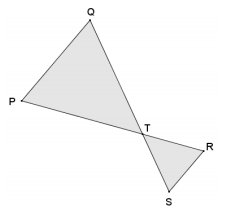
Answer:
Since PQRS is a cyclic quadrilateral, draw a circle on points P, Q, R, and S. ∠PQS and ∠PRS are angles inscribed in the same \(\widehat{S P}\); therefore, they are equal in measure. Also, ∠QPR and ∠QSR are both inscribed in the same \(\widehat{Q R}\); therefore, they are equal in measure. Therefore, by AA criterion for similar triangles, △PQT ~△SRT.
(Students may also use vertical angles relationship at T.)
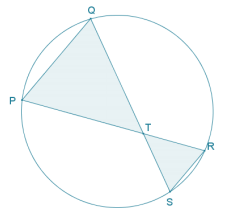
Exercise 3.
A cyclic quadrilateral has perpendicular diagonals. What is the area of the quadrilateral in terms of a, b, c, and d as shown?
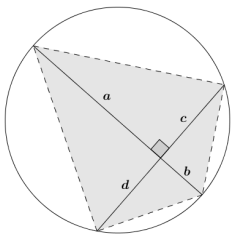
Answer:
Using the area formula for a triangle Area = \(\frac{1}{2}\) ⋅ base ⋅ height, the area of the quadrilateral is the sum of the areas of the four right triangular regions.
Area = \(\frac{1}{2}\) ac + \(\frac{1}{2}\) cb + \(\frac{1}{2}\) bd + \(\frac{1}{2}\) da
OR
Area = \(\frac{1}{2}\) (ac + cb + bd + da)
Exercise 4.
Show that the triangle in the diagram has area \(\frac{1}{2}\) ab sin(w).
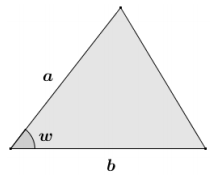
Answer:
Draw an altitude to the side with length b as shown in the diagram to form adjacent right triangles. Using right triangle trigonometry, the sine of the acute angle with degree measure w is
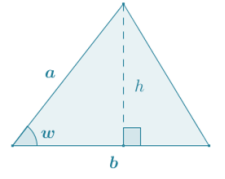
sin(w) = \(\frac{h}{a}\), where h is the length of the altitude to side b.
It then follows that h = a.
Using the area formula for a triangle:
Area = \(\frac{1}{2}\)×base×height
Area = \(\frac{1}{2}\) b(a sin(w) )
Area = \(\frac{1}{2}\) ab sin(w)
Exercise 5.
Show that the triangle with obtuse angle (180 – w)° has area \(\frac{1}{2}\) ab sin(w).
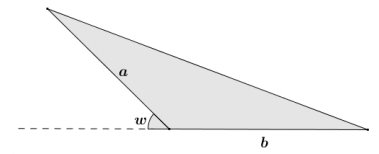
Answer:
Draw an altitude to the line that includes the side of the triangle with length b. Using right triangle trigonometry:
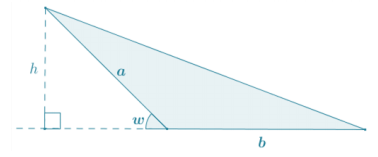
sin(w) = \(\frac{h}{a}\) , where h is the length of the altitude drawn.
It follows then that h = a sin(w).
Using the area formula for a triangle:
Area = \(\frac{1}{2}\)×base×height
Area = \(\frac{1}{2}\) b(a sin(w) )
Area = \(\frac{1}{2}\) ab sin(w)
Exercise 6.
Show that the area of the cyclic quadrilateral shown in the diagram is Area = \(\frac{1}{2}\)(a + b)(c + d)sin(w).
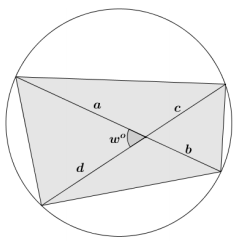
Answer:
Using the area formula for a triangle:
Area = \(\frac{1}{2}\) ab ⋅ sin(w)
Area1 = \(\frac{1}{2}\) ad ⋅ sin(w)
Area2 = \(\frac{1}{2}\) ac ⋅ sin(w)
Area3 = \(\frac{1}{2}\) bc ⋅ sin(w)
Area4 = \(\frac{1}{2}\) bd ⋅ sin(w)
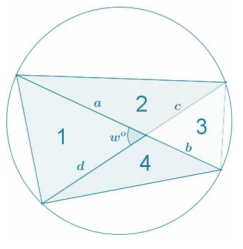
Areatotal = Area1 + Area2 + Area3 + Area4
Areatotal = \(\frac{1}{2}\) ad ⋅ sin(w) + \(\frac{1}{2}\) ac ⋅ sin(w) + \(\frac{1}{2}\) bc ⋅ sin(w) + \(\frac{1}{2}\) bd ⋅ sin(w)
Areatotal = [\(\frac{1}{2}\) sin(w) ](ad + ac + bc + bd)
Areatotal = [\(\frac{1}{2}\) sin(w) ][(a + b)(c + d)]
Areatotal = \(\frac{1}{2}\) (a + b)(c + d) sin(w)
Eureka Math Geometry Module 5 Lesson 20 Problem Set Answer Key
Question 1.
Quadrilateral BDCE is cyclic, O is the center of the circle, and m∠BOC = 130°. Find m∠BEC.
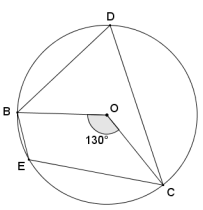
Answer:
By the inscribed angle theorem, m∠BDC = \(\frac{1}{2}\) m∠BOC, so m∠BDC = 65°.
Opposite angles of cyclic quadrilaterals are supplementary, so
m∠BEC + 65° = 180°. Thus, m∠BEC = 115°.
Question 2.
Quadrilateral FAED is cyclic, AX = 8, FX = 6, XD = 3, and m∠AXE = 130°. Find the area of quadrilateral FAED.
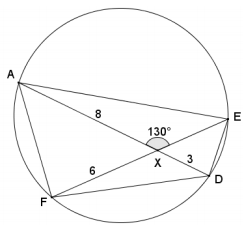
Answer:
Using the two – chord power rule, (AX)(XD) = (FX)(XE).
8(3) = 6(XE); thus, XE = 4.
The area of a cyclic quadrilateral is equal to the product of the lengths of the diagonals and the sine of the acute angle formed by them. The acute angle formed by the diagonals is 50°.
Area = \(\frac{1}{2}\)(8 + 3)(6 + 4) ⋅ sin(50)
Area = \(\frac{1}{2}\)(11)(10) ⋅ sin(50)
Area ≈ 42.1
The area of quadrilateral FAED is approximately 42.1 square units.
Question 3.
In the diagram below, \(\overline{B E}\)∥\(\overline{C D}\) and m∠BED = 72°. Find the value of s and t.
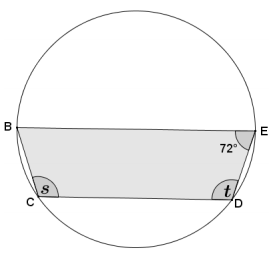
Answer:
Quadrilateral BCDE is cyclic, so opposite angles are supplementary.
s + 72° = 180°
s = 108°
Parallel chords \(\overline{B E}\) and \(\overline{C D}\) intercept congruent arcs \(\widehat{C B}\) and \(\widehat{E D}\). By angle addition, \(m\widehat{C B E}\) = \(\widehat{B E D}\), so it follows by the inscribed angle theorem that s = t = 108°.
Question 4.
In the diagram below, \(\overline{B C}\) is the diameter, m∠BCD = 25°, and \(\overline{C E}\) ≅ \(\overline{D E}\). Find m∠CED and m∠EDC.
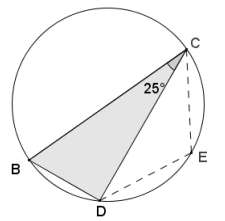
Answer:
Triangle BCD is inscribed in a semicircle. By Thales’ theorem, ∠BDC is a right angle. By the angle sum of a triangle, m∠DBC = 65°. Quadrilateral BCED is cyclic, so opposite angles are supplementary.
65° + m∠CED = 180°
m∠CED = 115°
Triangle CED is isosceles since \(\overline{C E}\) ≅ \(\overline{D E}\), and by base ∠’s, ∠EDC ≅ ∠ECD.
2(m∠EDC) = 180° – 115° by the angle sum of a triangle.
m∠EDC = 32.5°
Question 5.
In circle A, m∠ABD = 15°. Find m∠BCD.
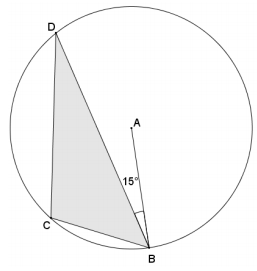
Answer:
Draw diameter \(\overline{B A X}\) such that X is on the circle, and then draw \(\overline{D X}\). Triangle BDX is inscribed in a semicircle; therefore, angle BDX is a right angle. By the angle sum of a triangle, m∠BXD = 75°.
Quadrilateral BCDX is a cyclic quadrilateral, so its opposite angles are supplementary.
m∠BCD + m∠BXD = 180°
m∠BCD + 75° = 180°
m∠BCD = 105°
Question 6.
Given the diagram below, O is the center of the circle. If m∠NOP = 112°, find m∠PQE.
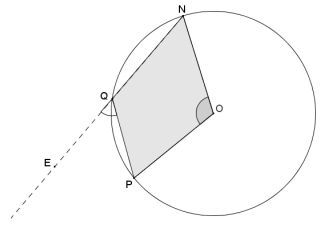
Answer:
Draw point X on major arc \(\widehat{N P}\), and draw chords \(\overline{X N}\) and \(\overline{X P}\) to form cyclic quadrilateral QuestionXP. By the inscribed angle theorem, m∠NXP = \(\frac{1}{2}\) m∠NOP, so m∠NXP = 56°.
An exterior angle PQE of cyclic quadrilateral QuestionXP is equal in measure to the angle opposite from vertex Q, which is ∠NXP. Therefore, m∠PQE = 56°.
Question 7.
Given the angle measures as indicated in the diagram below, prove that vertices C, B, E, and D lie on a circle.
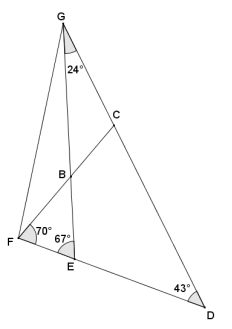
Answer:
Using the angle sum of a triangle, m∠FBE = 43°. Angles GBC and FBE are vertical angles and, therefore, have the same measure. Angles GBF and EBC are also vertical angles and have the same measure. Angles at a point sum to 360°, so m∠CBE = m∠FBG = 137°. Since 137 + 43 = 180, angles EBC and EDC of quadrilateral BCDE are supplementary. If a quadrilateral has opposite angles that are supplementary, then the quadrilateral is cyclic, which means that vertices C, B, E, and D lie on a circle.
Question 8.
In the diagram below, quadrilateral JKLM is cyclic. Find the value of n.
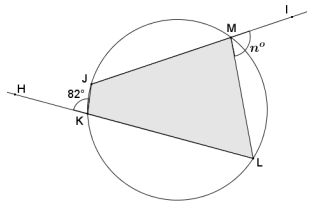
Answer:
Angles HKJ and LKJ form a linear pair and are supplementary, so angle LKJ has measure of 98°.
Opposite angles of a cyclic quadrilateral are supplementary; thus, m∠JML = m∠JKH = 82°.
Angles JML and IML form a linear pair and are supplementary, so angle IML has measure of 98°. Therefore, n = 98.
Question 9.
Do all four perpendicular bisectors of the sides of a cyclic quadrilateral pass through a common point? Explain.
Answer:
Yes. A cyclic quadrilateral has vertices that lie on a circle, which means that the vertices are equidistant from the center of the circle. The perpendicular bisector of a segment is the set of points equidistant from the segment’s endpoints. Since the center of the circle is equidistant from all of the vertices (endpoints of the segments that make up the sides of the cyclic quadrilateral), the center lies on all four perpendicular bisectors of the quadrilateral.
Question 10.
The circles in the diagram below intersect at points A and B. If m∠FHG = 100° and m∠HGE = 70°, find m∠GEF and m∠EFH.
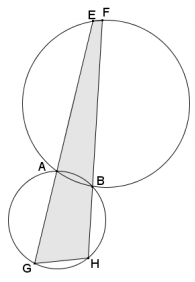
Answer:
Quadrilaterals GHBA and EFBA are both cyclic since their vertices lie on circles. Opposite angles in cyclic quadrilaterals are supplementary.
m∠GAB + m∠FHG = 180°
m∠GAB + 100° = 180°
m∠GAB = 80°
∠EAB and ∠GAB are supplementary since they form a linear pair, so
m∠EAB = 100°.
∠EAB and ∠EFB are supplementary since they are opposite angles in a cyclic quadrilateral, so m∠EFB = 80°.
Using a similar argument:
m∠HGE + m∠HBA = m∠HBA + m∠FBA = m∠FBA + m∠GEF = 180°
m∠HGE + m∠HBA = m∠HBA + m∠FBA = m∠FBA + m∠GEF = 180°
m∠HGE + m∠GEF = 180°
70° + m∠GEF = 180°
m∠GEF = 110°
Question 11.
A quadrilateral is called bicentric if it is both cyclic and possesses an inscribed circle. (See diagram to the right.)
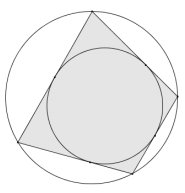
a. What can be concluded about the opposite angles of a bicentric quadrilateral? Explain.
Answer:
Since a bicentric quadrilateral must be also be cyclic, its opposite angles must be supplementary.
b. Each side of the quadrilateral is tangent to the inscribed circle. What does this tell us about the segments contained in the sides of the quadrilateral?
Answer:
Two tangents to a circle from an exterior point form congruent segments. The distances from a vertex of the quadrilateral to the tangent points where it meets the inscribed circle are equal.
c. Based on the relationships highlighted in part (b), there are four pairs of congruent segments in the diagram. Label segments of equal length with a, b, c, and d.
Answer:
See diagram on the right.
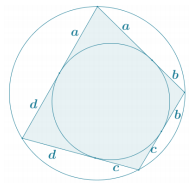
d. What do you notice about the opposite sides of the bicentric quadrilateral?
Answer:
The sum of the lengths of one pair of opposite sides of the bicentric quadrilateral is equal to the sum of the lengths of the other pair of opposite sides:
(a + b) + (c + d) = (d + a) + (b + c).
Question 12.
Quadrilateral PSRQ is cyclic such that \(\overline{P Q}\) is the diameter of the circle. If ∠QRT ≅ ∠QSR, prove that ∠PTR is a right angle, and show that S, X, T, and P lie on a circle.
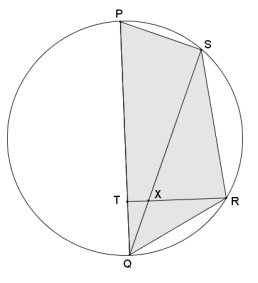
Answer:
Angles RQX and SQR are congruent since they are the same angle. Since it was given that ∠QRT ≅ ∠QSR, it follows that △QXR ~ △QRS by AA similarity criterion. Corresponding angles in similar figures are congruent, so ∠QRS ≅ ∠QXR, and by vertical ∠’s, ∠QXR ≅ ∠TXS.
Quadrilateral PSRQ is cyclic, so its opposite angles QPS and QRS are supplementary. Since ∠QXR ≅ ∠TXS, it follows that angles TXS and QPS are supplementary. If a quadrilateral has a pair of opposite angles that are supplementary, then the quadrilateral is cyclic. Thus, quadrilateral SXTP is cyclic.
Angle PSQ is a right angle since it is inscribed in a semi – circle. If a quadrilateral is cyclic, then its opposite angles are supplementary; thus, angle PTR must be supplementary to angle PSQ. Therefore, it is a right angle.
Eureka Math Geometry Module 5 Lesson 20 Exit Ticket Answer Key
Question 1.
What value of x guarantees that the quadrilateral shown in the diagram below is cyclic? Explain.
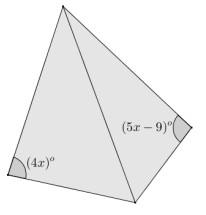
Answer:
4x + 5x – 9 = 180
9x – 9 = 180
9x = 189
x = 21
If x = 21, then the opposite angles shown are supplementary, and any quadrilateral with supplementary opposite angles is cyclic.
Question 2.
Given quadrilateral GKHJ, m∠KGJ + m∠KHJ = 180°, m∠HNJ = 60°, KN = 4, NJ = 48, GN = 8, and NH = 24, find the area of quadrilateral GKHJ. Justify your answer.
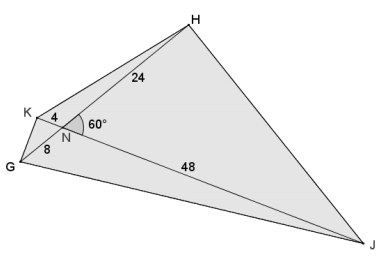
Answer:
Opposite angles KGJ and KHJ are supplementary, so quadrilateral GKHJ is cyclic.
The area of a cyclic quadrilateral:
Area = \(\frac{1}{2}\) (4 + 48)(8 + 24) ⋅ sin(60)
Area = \(\frac{1}{2}\)(52)(32) ⋅ \(\frac{\sqrt{3}}{2}\)
Area = \(\frac{\sqrt{3}}{4}\) ⋅ 1664
Area = 416\(\sqrt{3}\)
The area of quadrilateral GKHJ is 416\(\sqrt{3}\) square units.