Eureka Math Geometry Module 5 Lesson 13 Answer Key

/ By

Engage NY Eureka Math Geometry Module 5 Lesson 13 Answer Key

Eureka Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key

Exploratory Challenge
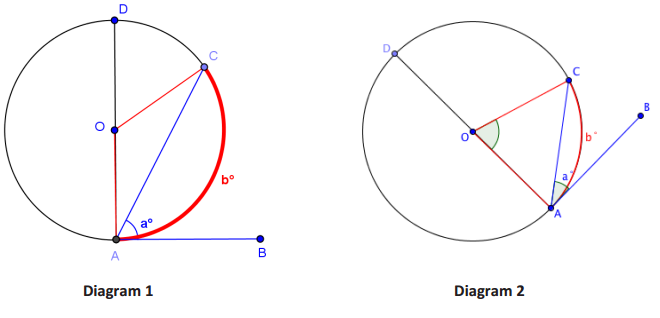
Engage NY Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key 1
Examine the diagrams shown. Develop a conjecture about the relationship between a and b.
a = \(\frac{1}{2}\) b

Test your conjecture by using a protractor to measure a and b.
Engage NY Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key 2
Answer:
Engage NY Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key 3

Do your measurements confirm the relationship you found in your homework?
If needed, revise your conjecture about the relationship between a and b:

Now, test your conjecture further using the circle below.
Engage NY Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key 4
Now, we will prove your conjecture, which is stated below as a theorem.
THE TANGENT – SECANT THEOREM: Let A be a point on a circle, let \(\overleftrightarrow{A B}\) be a tangent ray to the circle, and let C be a point on the circle such that \(\overleftrightarrow{A C}\) is a secant to the circle. If a = m∠BAC and b is the angle measure of the arc intercepted by ∠BAC, then a = \(\frac{1}{2}\) b.
Given circle O with tangent \(\overleftrightarrow{A B}\), prove what we have just discovered using what you know about the properties of a circle and tangent and secant lines.
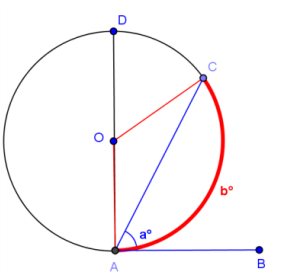
Engage NY Math Geometry Module 5 Lesson 13 Exploratory Challenge Answer Key 5
a. Draw triangle AOC. What is the measure of ∠AOC? Explain.
Answer:
b°. The central angle is equal to the degree measure of the arc it intercepts.

b. What is the measure of ∠OAB? Explain.
Answer:
90°. The radius is perpendicular to the tangent line at the point of tangency.

c. Express the measure of the remaining two angles of triangle AOC in terms of a and explain.
Answer:
The angles are congruent because the triangle is isosceles. Each angle has a measure of (90 – a)° since m∠OAC + m∠CAB = 90°.

d. What is the measure of ∠AOC in terms of a? Show how you got the answer.
Answer:
The sum of the angles of a triangle is 180°, so 90 – a + 90 – a + b = 180. Therefore, b = 2a or a = 1/2 b.

e. Explain to your neighbor what we have just proven.
Answer:
An inscribed angle formed by a secant and tangent line is half of the angle measure of the arc it intercepts.

Eureka Math Geometry Module 5 Lesson 13 Exercise Answer Key

Opening Exercise
In circle A, \(m \widehat{B D}\) = 56°, and (BC) ̅ is a diameter. Find the listed measure, and explain your answer.
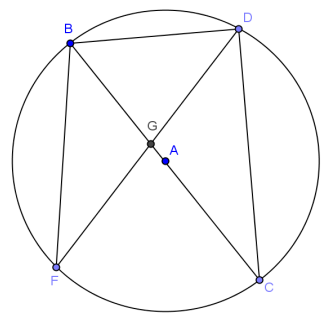
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 1
a. m∠BDC
Answer:
90°, angles inscribed in a diameter

b. m∠BCD
Answer:
28°, inscribed angle is half measure of intercepted arc

c. m∠DBC
Answer:
62°, sum of angles of a triangle is 180°

d. m∠BFG
Answer:
28°, inscribed angle is half measure of intercepted arc

e. \(m \widehat{B C}\)
Answer:
180°, semicircle

f. \(m \widehat{D C}\)
Answer:
124°, intercepted arc is double inscribed angle

g. Does ∠BGD measure 56°? Explain.
Answer:
No, the central angle of \( would be 56°. ∠BGD is not a central angle because its vertex is not the center of the circle.

h. How do you think we could determine the measure of ∠BGD?
Answer:
Answers will vary. This leads to today’s lesson.

Exercises

Exercise 1.
Find x, y, a, b, and/or c.
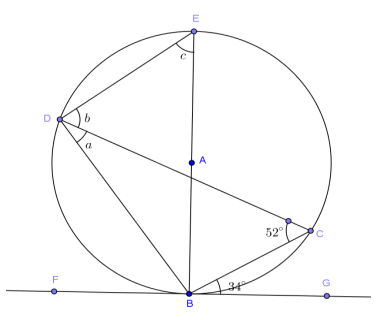
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 2
Answer:
a = 34°, b = 56°, c = 52°

Exercise 2.
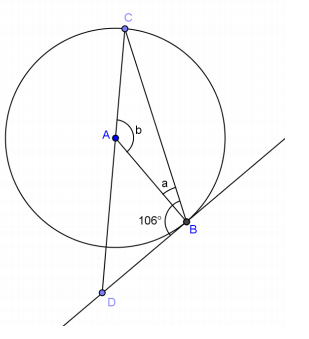
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 3
Answer:
a = 16°, b = 148°

Exercise 3.
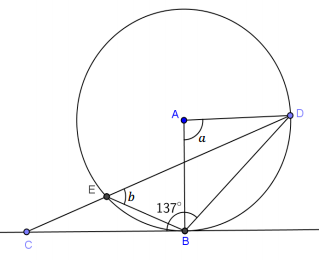
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 4
Answer:
a = 86°, b = 43°

Exercise 4.
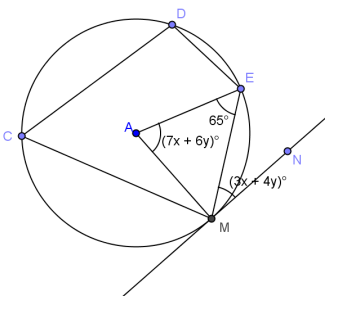
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 5
Answer:
2(3x + 4y) = 7x + 6y
65 + 65 + (7x + 6y) = 180
x = 5, y = 2.5

Exercise 5.
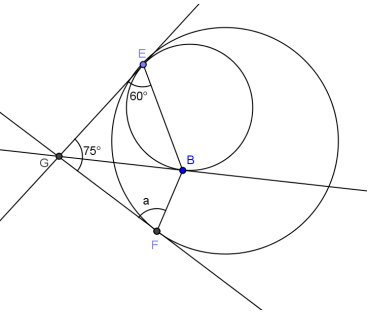
Engage NY Math Geometry Module 5 Lesson 13 Exercise Answer Key 6
Answer:
a = 60°

Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key

In Problems 1–9, solve for a, b, and/or c.
Question 1.
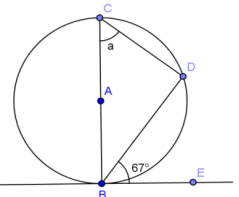
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 1
Answer:
a = 67°

Question 2.
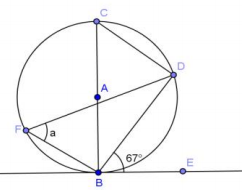
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 2
Answer:
a = 67°

Question 3.
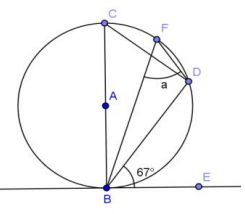
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 3
Answer:
a = 67°

Question 4.
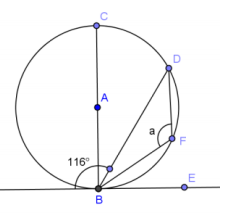
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 4
Answer:
a = 116°

Question 5.
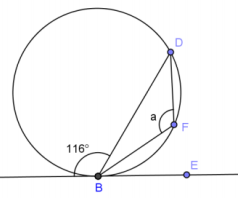
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 5
Answer:
a = 116°

Question 6.
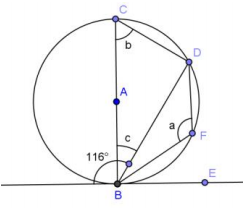
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 6
Answer:
a = 116°, b = 64°, c = 26°

Question 7.
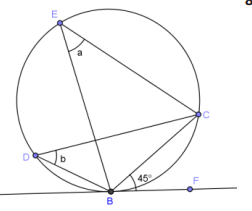
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 7
Answer:
a = 45°, b = 45°

Question 8.
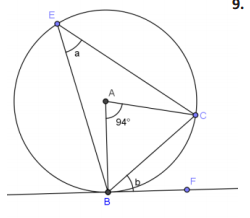
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 8
Answer:
a = 47°, b = 47°

Question 9.
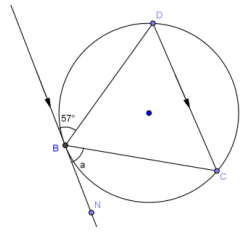
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 9
Answer:
a = 57°

Question 10.
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 12 is tangent to circle A. [latex]\overline{D F}\) is a diameter. Find the angle measurements.
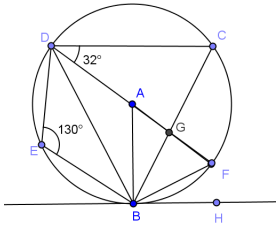
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 10
a. m∠BCD
Answer:
50°

b. m∠BAF
Answer:
80°

c. m∠BDA
Answer:
40°

d. m∠FBH
Answer:
40°

e. m∠BGF
Answer:
98°

Question 11.
\(\overline{B G}\) is tangent to circle A. \(\overline{B E}\) is a diameter. Prove: (i) f = a and (ii) d = c.
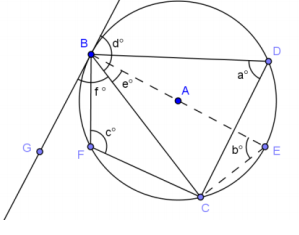
Eureka Math Geometry Module 5 Lesson 13 Problem Set Answer Key 11
Answer:
(i) m∠EBG = 90°    Tangent perpendicular to radius
f = 90 – e     Sum of angles
m∠ECB = 90°     Angle inscribed in semicircle
In â–³ECB,
b + 90 + e = 180     Sum of angles of a triangle
b = 90 – e
a = b     Angles inscribed in same arc are congruent
a = f     Substitution

(ii) a + c = 180     Inscribed in opposite arcs
a = f      Inscribed in same arc
f + d = 180      Linear pairs form supplementary angles
c + f = f + d    Substitution
c = d

Eureka Math Geometry Module 5 Lesson 13 Exit Ticket Answer Key

Question 1.
Find a, b, and c.
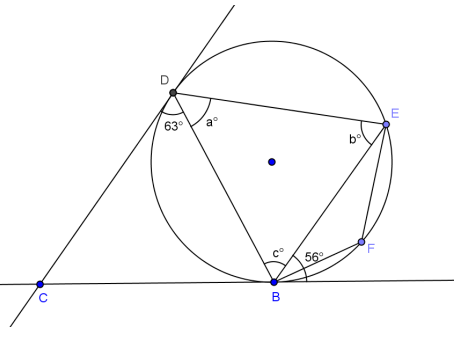
Eureka Math Geometry Module 5 Lesson 13 Exit Ticket Answer Key 1
Answer:
a = 56, b = 63, c = 61

Leave a Comment

Scroll to Top
Scroll to Top