Eureka Math Geometry Module 1 Lesson 4 Answer Key

Engage NY Eureka Math Geometry Module 1 Lesson 4 Answer Key

Eureka Math Geometry Module 1 Lesson 4 Exercise Answer Key

Opening Exercise
Choose one method below to check your Problem Set:
→ Trace your copied angles and bisectors onto patty paper; then, fold the paper along the bisector you constructed. Did one ray exactly overlap the other?
→ Work with your partner. Hold one partner’s work over another’s. Did your angles and bisectors coincide perfectly?
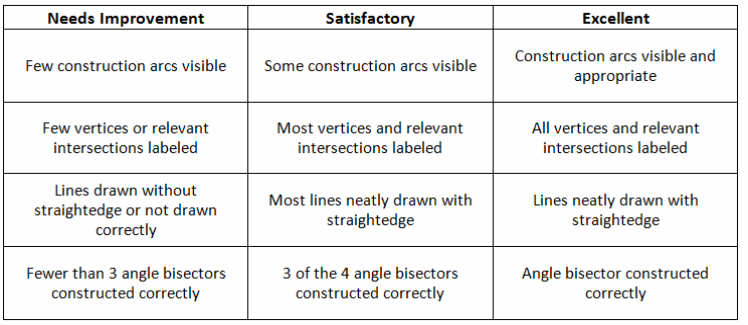
Use the following rubric to evaluate your Problem Set:

Discussion
In Lesson 3, we studied how to construct an angle bisector. We know we can verify the construction by folding an angle along the bisector. A correct construction means that one half of the original angle coincides exactly with the other half so that each point of one ray of the angle maps onto a corresponding point on the other ray of the angle.

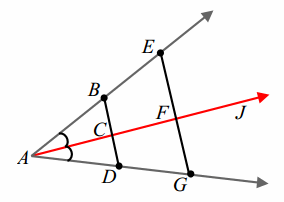
We now extend this observation. Imagine a segment that joins any pair of points that map onto each other when the original angle is folded along the bisector. The figure to the right illustrates two such segments.

Let us examine one of the two segments, \(\overline{E G}\). When the angle is folded along \(\overrightarrow{A J}\), E coincides with G. In fact, folding the angle demonstrates that E is the same distance from F as G is from F; EF=FG. The point that separates these equal halves of \(\overline{E G}\) is F, which is, in fact, the midpoint of the segment and lies on the bisector \(\overrightarrow{A J}\). We can make this case for any segment that falls under the conditions above.

By using geometry facts we acquired in earlier school years, we can also show that the angles formed by the segment and the angle bisector are right angles. Again, by folding, we can show that ∠EFJ and ∠GFJ coincide and must have the same measure. The two angles also lie on a straight line, which means they sum to 180°. Since they are equal in measure and sum to 180°, they each have a measure of 90°.

These arguments lead to a remark about symmetry with respect to a line and the definition of a perpendicular bisector. Two points are symmetric with respect to a line l if and only if l is the perpendicular bisector of the segment that joins the two points. A perpendicular bisector of a segment passes through the ___ of the segment and forms ___ with the segment.
Answer:
These arguments lead to a remark about symmetry with respect to a line and the definition of a perpendicular bisector. Two points are symmetric with respect to a line l if and only if l is the perpendicular bisector of the segment that joins the two points. A perpendicular bisector of a segment passes through the midpoint of the segment and forms right angles with the segment.

We now investigate how to construct a perpendicular bisector of a line segment using a compass and a straightedge. Using what you know about the construction of an angle bisector, experiment with your construction tools and the following line segment to establish the steps that determine this construction.

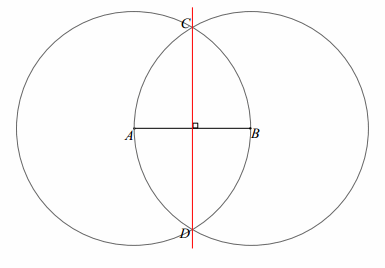
Answer:
Precisely describe the steps you took to bisect the segment.
1. Label the endpoints of the segment A and B.
2. Draw circle A: center A, radius AB, and circle B: center B, radius BA.
3. Label the points of intersections as C and D.
4. Draw \(\overleftrightarrow{\boldsymbol{C D}}\).

Now that you are familiar with the construction of a perpendicular bisector, we must make one last observation. Using your compass, string, or patty paper, examine the following pairs of segments:
i. \(\overline{A C}\), \(\overline{B C}\)
ii. \(\overline{A D}\), \(\overline{B D}\)
iii. \(\overline{A E}\), \(\overline{B E}\)
Based on your findings, fill in the observation below.

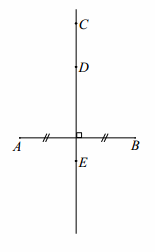
Observation:
Any point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
Answer:
Any point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.

Mathematical Modeling Exercise
You know how to construct the perpendicular bisector of a segment. Now, investigate how to construct a perpendicular to a line l from a point A not on l. Think about how you have used circles in constructions so far and why the perpendicular bisector construction works the way it does. The first step of the instructions has been provided for you. Discover the construction, and write the remaining steps.

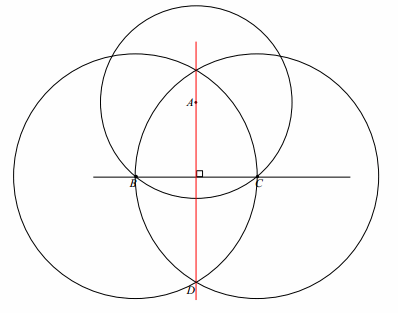
Step 1. Draw circle A: center A with radius so that circle A intersects line l in two points.
Answer:
Step 2: Label the two points of intersection as B and C.
Step 3: Draw circle B: center B, radius BC.
Step 4: Draw circle C: center C, radius CB.
Step 5: Label one of the unlabeled intersections of circle B and circle C as D.
Step 6: Draw \(\overleftrightarrow{A D}\).

Relevant Vocabulary

RIGHT ANGLE: An angle is called a right angle if its measure is 90°.

PERPENDICULAR: Two lines are perpendicular if they intersect in one point and if any of the angles formed by the intersection of the lines is a 90° (right) angle. Two segments or rays are perpendicular if the lines containing them are perpendicular lines.

EQUIDISTANT: A point A is said to be equidistant from two different points B and C if AB=AC. A point A is said to be equidistant from a point B and a line l if the distance between A and l is equal to AB.

Eureka Math Geometry Module 1 Lesson 4 Problem Set Answer Key

Question 1.
During this lesson, you constructed a perpendicular line to a line l from a point A not on l. We are going to use that construction to construct parallel lines.
To construct parallel lines l₁ and l₂:
i. Construct a perpendicular line l₃ to a line l₁ from a point A not on l₁.
ii. Construct a perpendicular line l₂ to l₃ through point A. Hint: Consider using the steps behind Problem 4 in the Lesson 3 Problem Set to accomplish this.

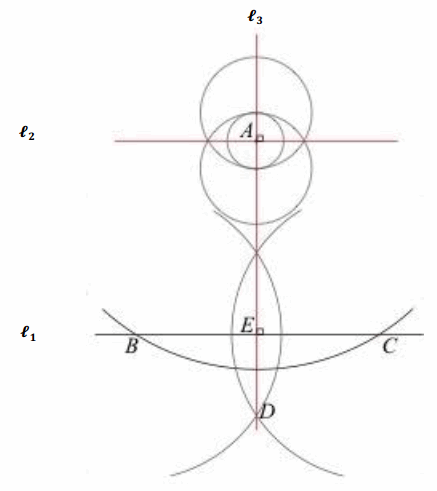
Question 2.
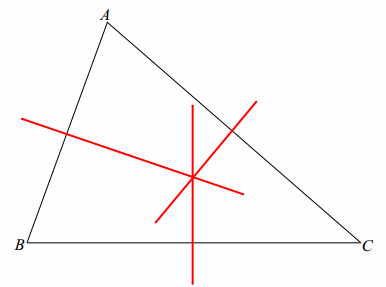
Construct the perpendicular bisectors of \(\overline{A B}\), \(\overline{B C}\), and \(\overline{C A}\) on the triangle below. What do you notice about the segments you have constructed?
Answer:
Students should say that the three perpendicular bisectors pass through a common point. (Students may additionally conjecture that this common point is equidistant from the vertices of the triangle.)

Question 3.
Two homes are built on a plot of land. Both homeowners have dogs and are interested in putting up as much fencing as possible between their homes on the land but in a way that keeps the fence equidistant from each home. Use your construction tools to determine where the fence should go on the plot of land. How must the fencing be altered with the addition of a third home?
Answer:

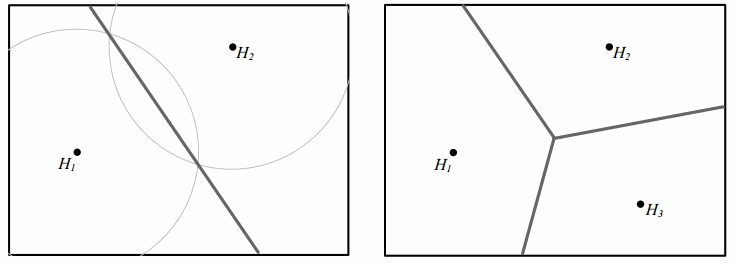
Eureka Math Geometry Module 1 Lesson 4 Exit Ticket Answer Key

Divide the following segment AB into four segments of equal length.

Answer: