Engage NY Eureka Math Geometry Module 5 Lesson 12 Answer Key
Eureka Math Geometry Module 5 Lesson 12 Example Answer Key
Example
In each diagram, try to draw a circle with center D that is tangent to both rays of ∠BAC.
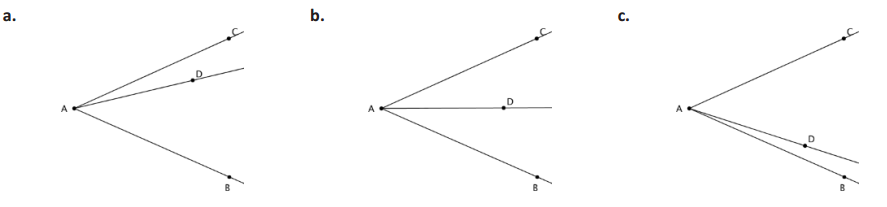
In which diagrams did it seem impossible to draw such a circle? Why did it seem impossible?
Answer:
(a) Impossible; (b) possible; (c) impossible. It is not possible to draw a circle tangent to both rays of the angle in (a) and (c) because D is a different distance from the two sides of the angle. The distance is the radius of a circle tangent to that side.
What do you conjecture about circles tangent to both rays of an angle? Why do you think that?
Answer:
If a circle is tangent to both rays of an angle, then the center lies on the angle bisector. We saw this in all examples.
Eureka Math Geometry Module 5 Lesson 12 Exercise Answer Key
Opening Exercise
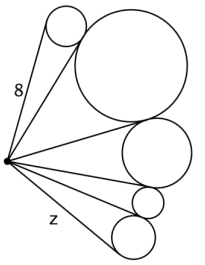
In the diagram, what do you think the length of z could be? How do you know?
Answer:
z = 8 because each successive segment is tangent to the same circle, so the segments are congruent.
Exercises
Exercise 1.
You conjectured that if a circle is tangent to both rays of a circle, then the center lies on the angle bisector.
a. Rewrite this conjecture in terms of the notation suggested by the diagram.
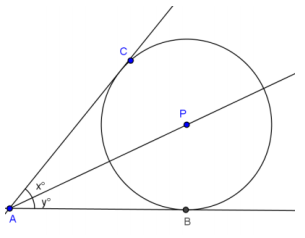
Answer:
Given:
Circle with center P and tangent to \(\overline{A B}\) and \(\overline{A C}\);
x = m∠CAP; y = ∠BAP
Need to show:
x = y
b. Prove your conjecture using a two-column proof.
Answer:
m∠CAP = x, m∠BAP = y Given
\(\overline{P C}\) ⊥ \(\overline{A C}\), \(\overline{P B}\) ⊥ \(\overline{A B}\) Tangent is perpendicular to the radius at the point of tangency.
△ABP and △ACP are right triangles. Definition of right triangle
AP = AP Reflexive property
PB = PC Radii of the same circle are equal in length.
△ABP ≅ △ACP HL
m∠BAP = m∠CAP Corresponding angles of congruent triangles are equal in measure.
x = y Substitution
\(\overline{A P}\) bisects ∠CAB Definition of angle bisector
Exercise 2.
An angle is shown below.
a. Draw at least three different circles that are tangent to both rays of the given angle.
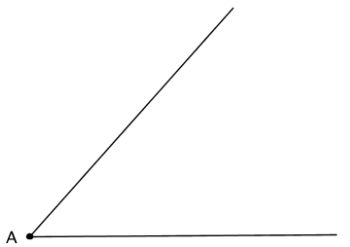
Answer:
Many circles are possible. The main idea is that the center must be a point on the angle bisector, and the radius is the perpendicular from the center to the rays of the angle.
b. Label the center of one of your circles with P. How does the distance between P and the rays of the angle compare to the radius of the circle? How do you know?
Answer:
The distance between P and the rays of the angle is the same length as the radius of the circle because it is perpendicular to tangent segments as proved in the last lesson.
Exercise 3.
Construct as many circles as you can that are tangent to both the given angles at the same time. You can extend the rays as needed. These two angles share a side.
Explain how many circles you can draw to meet the above conditions and how you know.
Answer:
There is only one circle. The center of the circle has to be on the angle bisector of each angle; the angle bisectors only intersect in one point. There is only one circle with that point as a center that is tangent to the rays. It is the one with the radius you get by dropping the perpendicular from the intersection of the angle bisectors (incenter) to the side \(\overline{A C}\).
Exercise 4.
In a triangle, let P be the location where two angle bisectors meet. Must P be on the third angle bisector as well? Explain your reasoning.
Answer:
The angle bisectors of any two consecutive angles are the same distance from both rays of both angles. Let the vertices of the triangle be A, B, and C where m∠A = 2x, m∠B = 2y, and ∠C = 2z. If point P is on the angle bisector of ∠A and ∠B, then it is the same distance from \(\overline{A B}\)and \(\overline{A C}\), and it is the same distance from \(\overline{B A}\) and \(\overline{B C}\). Thus, it is the same distance from \(\overline{C A}\) and \(\overline{C B}\); therefore, it is on the angle bisector of ∠C
Exercise 5.
Using a straightedge, draw a large triangle ABC.
a. Construct a circle inscribed in the given triangle.
Answer:
Construct angle bisectors between any two angles. Their intersection point will be the center of the circle. Drop a perpendicular from the intersection point to any side. This will be a radius. Draw the circle with that center and radius.
b. Explain why your construction works.
Answer:
The point P from Exercise 4 is the same distance from all three sides of △ABC. Thus, the perpendicular segments from P to each side are the same length. A line is tangent to a circle if and only if the line is perpendicular to a radius where the radius meets the circle. Therefore, a circle with center P and radius the length of the perpendicular segments from P to the sides is inscribed in the triangle.
c. Do you know another name for the intersection of the angle bisectors in relation to the triangle?
Answer:
The intersection of the angle bisectors is the incenter of the triangle.
Eureka Math Geometry Module 5 Lesson 12 Problem Set Answer Key
Question 1.
On a piece of paper, draw a circle with center A and a point, C, outside of the circle.
a. How many tangents can you draw from C to the circle?
Answer:
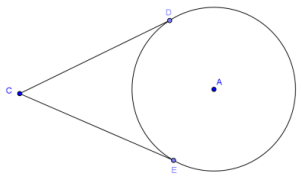
2 tangents
b. Draw two tangents from C to the circle, and label the tangency points D and E. Fold your paper along the line AC. What do you notice about the lengths of \(\overline{C D}\) and \(\overline{C E}\) ? About the measures of ∠DCA and ∠ECA?
Answer:
The lengths are the same; the angles are congruent.
c. \(\overline{A C}\) is the _____________________ of ∠DCE.
Answer:
Angle bisector
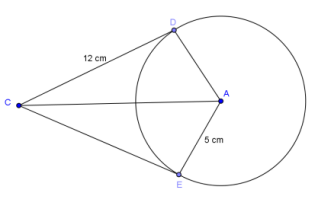
d. \(\overline{C D}\) and \(\overline{C E}\) are tangent to circle A. Find AC.
Answer:
AC = 13 by the Pythagorean theorem.
Question 2.
In the figure, the three segments are tangent to the circle at points B, F, and G. If y = 2/3 x, find x, y, and z.
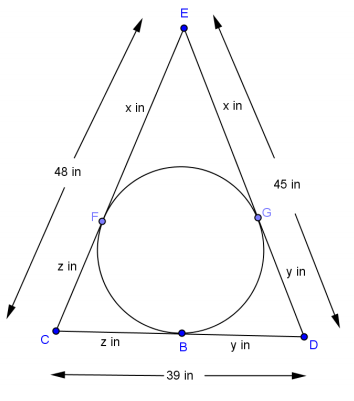
Answer:
Tangents to a circle from a given point are congruent.
So, EF = EG = x, GD = BD = y, and BC = CF = z.
This allows us to set up a system of simultaneous linear equations that can be solved for x, y, and z.
x + z = 48
x + y = 45
y + z = 39
x = 27,y = 18,z = 21
Question 3.
In the figure given, the three segments are tangent to the circle at points J, I, and H.
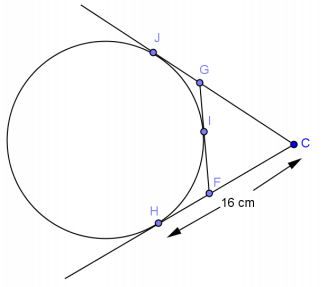
a. Prove GF = GJ + HF.
Answer:
GJ = GI and FI = HF because tangents to a circle from a given point are congruent.
GF = GI + FI sum of segments
GF = GJ + HF by substitution
b. Find the perimeter of △GCF.
Answer:
CH = 16 cm
GJ = GI,FI = HF,CJ = CH tangents to a circle from a given point are congruent.
CJ = GC + GJ, CH = CF + HF sum of segments
Perimeter = GC + CF + GF
GC + CF + (GI + FI) by substitution
GC + GI + CF + FI
GC + GJ + CF + HF by substitution
CJ + CH by substitution
2CH = 2(16 cm) = 32 cm
Question 4.
In the figure given, the three segments are tangent to the circle at points F, B, and G. Find DE.
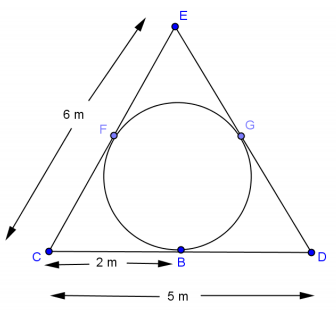
Answer:
7 m
Question 5.
\(\overleftrightarrow{E F}\) is tangent to circle A. If points C and D are the intersection points of circle A and any line parallel to \(\overleftrightarrow{E F}\), answer the following.
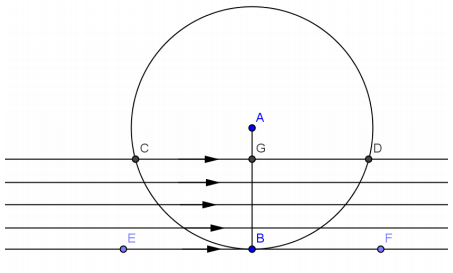
a. Does CG = GD for any line parallel to \(\overleftrightarrow{E F}\)? Explain.
Answer:
Yes. No matter what, △ACD is an isosceles triangle, and \(\overline{A G}\) is the altitude to the base of the triangle and, therefore, the angle bisector of the angle opposite the base.
b. Suppose that \(\overleftrightarrow{C D}\) coincides with \(\overleftrightarrow{E F}\). Would C, G, and D all coincide with B?
Answer:
Yes. If they approached B at different times, then at some point G would not be on the same line as C and D, but G is defined to be contained in the chord \(\overline{C D}\).
c. Suppose C, G, and D have now reached B, so \(\overleftrightarrow{C D}\) is tangent to the circle. What is the angle between \(\overleftrightarrow{C D}\) and \(\overline{A B}\)?
Answer:
90°. A line tangent to a circle is perpendicular to the radius at the point of tangency.
d. Draw another line tangent to the circle from some point, P, in the exterior of the circle. If the point of tangency is point T, what is the measure of ∠PTA?
Answer:
The measure of ∠PTA is 90° because a line tangent to a circle is perpendicular to a radius through the tangency point.
Question 6.
The segments are tangent to circle A at points B and D. \(\overline{E D}\) is a diameter of the circle.
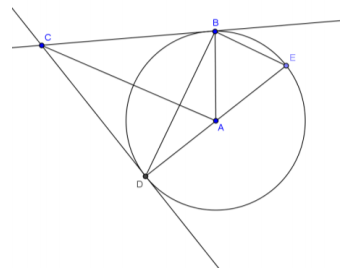
a. Prove \(\overline{B E}\) ∥ \(\overline{C A}\).
Answer:
m∠ABE = m∠E Base angles of an isosceles triangle are equal in measure.
m∠E = \(\frac{1}{2}\) m∠BAD Inscribed angle is half the central angle that intercepts the same arc.
m∠ABE = \(\frac{1}{2}\) m∠BAD Substitution
\(\overline{A C}\) bisects ∠BAD If a circle is tangent to both rays of an angle, then its center lies on the angle
bisector.
m∠ABE = m∠BAC Substitution
\(\overline{B E}\) ∥ \(\overline{B E}\) If two lines are cut by a transversal such that the alternate interior angles are
congruent, then the lines are parallel.
b. Prove quadrilateral ABCD is a kite.
Answer:
CB = CD Tangents to a circle from a given point are equal in measure.
AB = AD Radii are congruent.
Quadrilateral ABCD is a kite because two pairs of adjacent sides are congruent.
Question 7.
In the diagram shown, \(\overleftrightarrow{B H}\) is tangent to the circle at point B. What is the relationship between ∠DBH, the angle between the tangent and a chord, and the arc subtended by that chord and its inscribed angle ∠DCB?
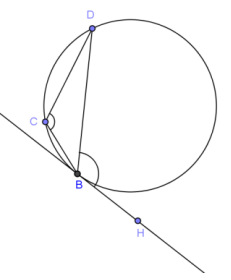
Answer:
m∠DBH = m∠DCB
Eureka Math Geometry Module 5 Lesson 12 Exit Ticket Answer Key
Question 1.
Draw a circle tangent to both rays of this angle.
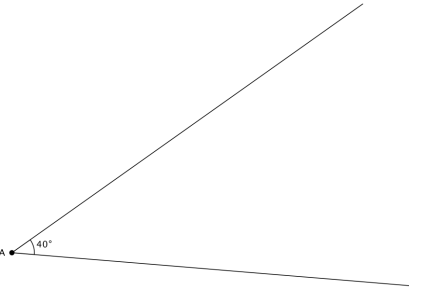
Answer:
Many circles are possible. Check that the center of the circle is on the angle bisector and the radius is from a perpendicular from the center to a ray of the angle.
Question 2.
Let B and C be the points of tangency of your circle. Find the measures of ∠ABC and ∠ACB. Explain how you determined your answer.
Answer:
△ABC is isosceles because the tangent segments AB and AC are congruent, so
m∠ABC = m∠ACB = \(\frac{180^{\circ}-40^{\circ}}{2}\) = 70°.
Question 3.
Let P be the center of your circle. Find the measures of the angles in △APB.
Answer:
In △APB, the angle at A measures 20°, at P measures 70°, and at B measures 90°.