Engage NY Eureka Math Geometry Module 4 Lesson 1 Answer Key
Eureka Math Geometry Module 4 Lesson 1 Exploratory Challenge Answer Key
Exploratory Challenge
Students in a robotics class must program a robot to move about an empty rectangular warehouse. The program specifies location at a given time, t seconds. The room is twice as long as it is wide. Locations are represented as points in a coordinate plane with the southwest corner of the room deemed the origin, (0, 0), and the northeast corner deemed the point (2000, 1000) in feet, as shown in the diagram below.
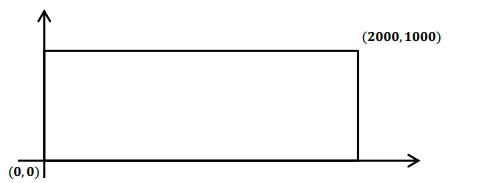
The first program written has the robot moving at a constant speed in a straight line. At time t = 1 second, the robot is at position (30, 45), and at t = 3 seconds, it is at position (50, 75). Complete the exercises, and answer the questions below to program the robot’s motion.
a. At what location will the robot hit the wall?
Answer:
It is at position (666 \(\frac{2}{3}\), 1000).
b. At what speed will the robot hit the wall?
Answer:
It will hit at approximately 18 ft/sec.
c. At what time will the robot hit the wall?
Answer:
It will hit at about t = 64.8 seconds.
Eureka Math Geometry Module 4 Lesson 1 Exercise Answer Key
Exercises
Exercise 1.
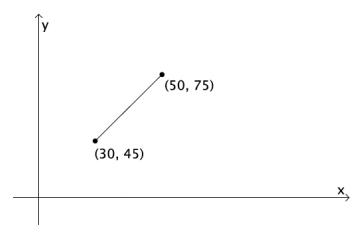
Plot the points on a coordinate plane.
Answer:
Exercise 2.
Draw the segment connecting the points.
Answer:

Exercise 3.
How much did the x – coordinate change in 2 seconds?
Answer:
It changed 20 ft.
Exercise 4.
How much did the y – coordinate change in 2 seconds.
Answer:
It changed 30 ft.
Exercise 5.
What is the ratio of change in y to the change in x?
Answer:
The ratio of change is \(\frac{3}{2}\)
Exercise 6.
What is the equation of the line of motion?
Answer:
The equation is y = \(\frac{3}{2}\)x.
Exercise 7.
What theorem could be used to find the distance between the points?
Answer:
The Pythagorean theorem could be used.
Exercise 8.
How far did the robot travel in 2 seconds?
Answer:
It traveled approximately 36.06 ft.
Eureka Math Geometry Module 4 Lesson 1 Problem Set Answer Key
Question 1.
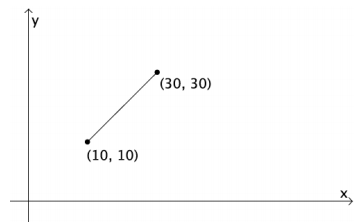
A robot from the video now moves around an empty 100 ft. by 100 ft. storage room at a constant speed. If the robot crosses (10, 10) at 1 second and (30, 30) at 6 seconds:
a. Plot the points, and draw the segment connecting the points.
Answer:
b. What was the change in the x – coordinate?
Answer:
It changed 20 ft.
c. What was the change in the y – coordinate?
Answer:
It changed 20 ft.
d. What is the ratio of the change in y to the change in x?
Answer:
The ratio of change is 1:1.
e. How far did the robot travel between the two points?
Answer:
It traveled approximately 28.28 ft.
f. What was the speed of the robot?
Answer:
The speed was approximately 5.66 ft/sec.
g. Where did the robot start?
Answer:
The robot started at position (6, 6).
Question 2.
Your mother received a robot vacuum cleaner as a gift and wants you to help her program it to clean a vacant 30 ft. by 30 ft. room. If the vacuum is at position (12, 9) at time t = 2 seconds and at position (24, 18) at t = 5 seconds, answer the following:
a. How far did the robot travel over 3 seconds?
Answer:
It traveled 15 ft.
b. What is the constant speed of the robot?
Answer:
The speed is 5 ft/sec.
c. What is the ratio of the change in the x – coordinate to the change in the y – coordinate?
Answer:
The ratio of change is \(\frac{4}{3}\), or y = \(\frac{3}{4}\) x.
d. Where did the robot start?
Answer:
It started at position (4, 3).
e. Where will the robot be at t = 3 seconds? Explain how you know.
Answer:
It will be at position (16, 12). I know that each second the x – value changed 4 units, and the y – value changed 3 units. The x – value started at 4; therefore, in 3 seconds, it increased 3×4 units, which means the x – value at 3 seconds is 4 + 12, or 16. The y – value started at 3 and increased 3×3 units, giving a y – value of 3 + 9, or 12.
f. At what location will the robot hit the wall?
Answer:
The location of impact is (30, 22 \(\frac{1}{2}\)).
g. At what time will the robot hit the wall?
Answer:
It will hit the wall at about t = 6.5 seconds.
Question 3.
A baseball player hits a ball at home plate at position (0, 0). It travels at a constant speed across first base at position (90, 0) in 2 seconds.
a. What was the speed of the ball?
Answer:
The speed was 45 ft/sec.
b. When will it cross the fence at position (300, 0)? Explain how you know.
Answer:
It will cross the fence in approximately 6.67 seconds. I know because the distance is 300 feet at a constant speed of 45 ft/sec. 300 ÷ 45 ≈ 6.67.
c. The tennis team has a robot that picks up tennis balls. The tennis court is 36 feet wide and 78 feet long. The robot starts at position (8, 10) and is at position (16, 20) at t = 4 seconds after moving at a constant speed. When will it pick up the ball located at position (28, 35)?
Answer:
It will pick up that ball in approximately 10 seconds.
Eureka Math Geometry Module 4 Lesson 1 Exit Ticket Answer Key
You are moving the robot to your classroom, which measures 30 feet by 40 feet.
Question 1.
Draw the classroom set up on a coordinate plane using (30, 40) as the northeast vertex.
Answer:
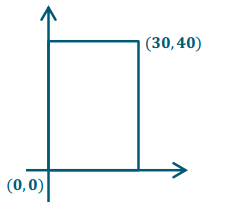
Question 2.
The robot was initially placed at position (6, 9), and at t = 2 seconds, its position is (10, 15).
a. How far did the robot travel in 2 seconds?
Answer:
It traveled approximately 7.2 ft.
b. What is the speed of the robot?
Answer:
The speed is approximately 3.6 ft/sec.