Eureka Math Geometry Module 4 End of Module Assessment Answer Key

Engage NY Eureka Math Geometry Module 4 End of Module Assessment Answer Key

Eureka Math Geometry Module 4 End of Module Assessment Task Answer Key

For problems that require rounding, round answers to the nearest hundredth.

Question 1.
Given parallelogram RSTU with vertices R(1, 3), S( – 2, – 1), T(4, 0), and U(7, 4):

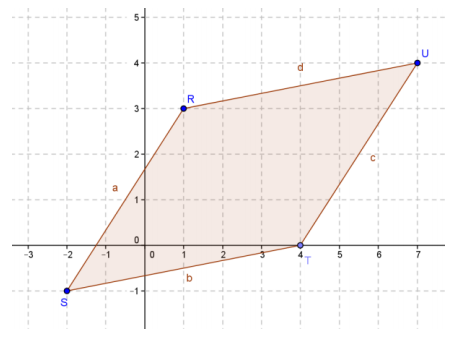
a. Find the perimeter of the parallelogram; round to the nearest hundredth.
Answer:
22.17 units

b. Find the area of the parallelogram.
Answer:
21 square units

Question 2.
Given triangle ABC with vertices A(6, 0), B( – 2, 2), and C( – 3, – 2):

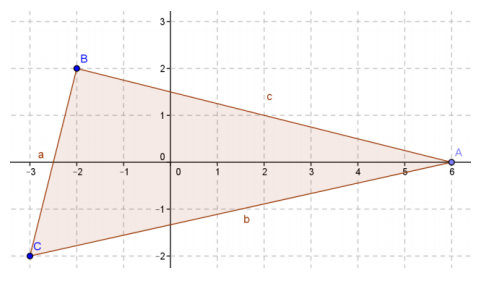
a. Find the perimeter of the triangle; round to the nearest hundredth.
Answer:
21.59 units

b. Find the area of the triangle.
Answer:
17 square units

Question 3.
A triangular region in the coordinate plane is defined by the system of inequalities
y ≥ \(\frac{1}{2}\) x – 6, y ≤ – 2x + 9, y ≤ 8x + 9.
a. Determine the coordinates of the vertices or the triangle.
Answer:
(0, 9) , (6, -3) , (-2, -7)

b. Sketch the triangular region defined by these inequalities.

Answer:

c. Is the triangle defined by the inequalities a right triangle? Explain your answer.
Answer:
Yes, given A (0, 9) , B (6, -3) , and C (-2, -7) , the slopes of \(\overline{A B}\) and \(\overline{B C}\) are negative reciprocals, so they are perpendicular. AB ² + BC ² = AC ² ; therefore, the converse of the Pythagorean theorem is true, meaning it is a right triangle.

d. Find the perimeter of the triangular region defined by the inequalities; round to the nearest hundredth.
Answer:
38.49 units

e. What is the area of this triangular region?
Answer:
60 square units

f. Of the three altitudes of the triangular region defined by the inequalities, what is the length of the shortest of the three? Round to the nearest hundredth.
Answer:
Altitudes: from ∠A = 13.42 , from ∠C = 8.94 , from ∠B = 7.44 (shortest)

Question 4.
Find the point on the directed line segment from (0, 3) to (6, 9) that divides the segment in the ratio of 2 : 1.
Answer:
(4, 7)

Question 5.
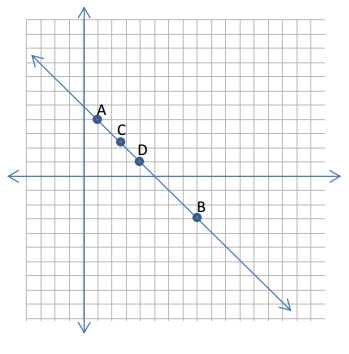
Consider the points A(1, 4) and B(8, – 3). Suppose C and D are points on the line through A and B satisfying \(\frac{AC}{CB}\) = \(\frac{1}{3}\) and \(\frac{BD}{DA}\) = \(\frac{4}{3}\), respectively.

a. Draw a sketch of the four collinear points A, B, C, and D, showing their relative positions to one another.
Answer:

b. Find the coordinates of point C.
Answer:
(\(\frac{11}{4}\), \(\frac{9}{4}\))

c. Find the coordinates of point D.
Answer:
(4, 1)

Question 6.
Two robots are left in a robotics competition. Robot A is programmed to move about the coordinate plane at a constant speed so that, at time t seconds, its position in the plane is given by
(0, 10) + \(\frac{t}{8}\) (60, 80).
Robot B is also programmed to move about the coordinate plane at a constant speed. Its position in the plane at time t seconds is given by
(70, 0) – \(\frac{t}{10}\) (70, – 70).

a. What was each robot’s starting position?
Answer:
A (0, 10),B (70, 0)

b. Where did each robot stop?
Answer:
A (60, 90), B (0, 70)

c. What is the equation of the path of robot A?
Answer:
y = \(\frac{4}{3}\) x + 10

d. What is the equation of the path of robot B?
Answer:
y = -x + 70

e. What is the speed of robot A? (Assume coordinates in the plane are given in units of meters. Give the speed in units of meters per second.)
Answer:
Distance = 100 m ; time = 8 seconds; speed = 12.5 m/sec

f. Do the two robots ever pass through the same point in the plane? Explain. If they do, do they pass through that common point at the same time? Explain.
Answer:
The robots both pass through the point (25 \(\frac{5}{7}\), 44 \(\frac{2}{7}\)). Robot A passes through that point at 3.43 seconds and robot B at 6.33 seconds. So, the robots do not pass through the point at the same time.

g. What is the closest distance robot B will ever be to the origin? Round to the nearest hundredth.
Answer:
The closest point that the robot will be to the origin is (35, 35), and that is a distance of 49.50 meters.

h. At time t = 10, robot A will instantaneously turn 90 degrees to the left and travel at the same constant speed it was previously traveling. What will be its coordinates in another 10 seconds’ time?
Answer:
At 10 seconds, robot A will be at (75, 110) . After turning 90° and continuing for another 10 seconds, the robot will be at (-25, 185) .

Question 7.
GDAY is a rhombus. If point G has coordinates (2, 6) and A has coordinates (8, 10), what is the equation of the line that contains the diagonal \(\overline{D Y}\) of the rhombus?
Answer:
Slope of \(\overline{G A}\) is \(\frac{2}{3}\); the diagonal will be perpendicular to \(\overline{G A}\) and bisect it, so the slope of \(\overline{D Y}\) is –\(\frac{3}{2}\), and it passes through the point (5, 8). The equation of the line is
3x + 2y = 31 .

Question 8.
a. A triangle has vertices A(a₁, a₂), B(b₁, b₂), and C(c₁, c₂). Let M be the midpoint of \(\overline{A C}\) and N the midpoint of \(\overline{B C}\). Find a general expression for the slope of \(\overline{M N}\). What segment of the triangle has the same slope as \(\overline{M N}\)?
Answer:
M (\(\frac{a_{1}+c_{1}}{2}, \frac{a_{2}+c_{2}}{2}\)), N (\(\frac{b_{1}+c_{1}}{2}, \frac{b_{2}+c_{2}}{2}\) )

Slope \(\overline{M N}\) = \(\frac{\frac{b_{2}+c_{2}}{2}-\frac{a_{2}+c_{2}}{2}}{\frac{b_{1}+c_{1}}{2}-\frac{a_{1}+c_{1}}{2}}=\frac{b_{2}-a_{2}}{b_{1}-a_{1}}\)

Slope \(\overline{M N}\) is the same as slope of \(\overline{A B}\).

b. A triangle has vertices A(a₁, a₂), B(b₁, b₂ ), and C(c₁, c₂ ). Let P be a point on \(\overline{A C}\) with AP = \(\frac{5}{8}\) AC, and let Q be a point on \(\overline{B C}\) with BQ = \(\frac{5}{8}\) BC. Find a general expression for the slope of \(\overline{P Q}\). What segment of the triangle has the same slope as \(\overline{P Q}\)?
Answer:
P (a₁ + \(\frac{5}{8}\)( c₁ -a₁ ), a₂ + \(\frac{5}{8}\)( c₂ -a₂)),Q (b₁ + \(\frac{5}{8}\) ( c₁ -b₁), b₂ + \(\frac{5}{8}\) ( c₂ -b₂))

Slope \(\overline{P Q}\)= \(\frac{\frac{3 b_{2}}{8}-\frac{3 a_{2}}{8}}{\frac{3 b_{1}}{8}-\frac{3 a_{1}}{8}}=\frac{b_{2}-a_{2}}{b_{1}-a_{1}}\)

Slope \(\overline{P Q}\)is the same as the slope of \(\overline{A B}\).

c. A quadrilateral has vertices A(a₁, a₂), B(b₁, b₂ ), C(c₁, c₂ ), and D(d₁, d₂ ). Let R, S, T, and U be the midpoints of the sides \(\overline{A B}\), \(\overline{B C}\), \(\overline{C D}\), and \(\overline{D A}\), respectively. Demonstrate that \(\overline{R S}\) is parallel to \(\overline{T U}\). Is \(\overline{S T}\) parallel to \(\overline{U R}\)? Explain.
Answer:
Slope \(\overline{R S}\)= \(\frac{\frac{b_{2}+c_{2}}{2}-\frac{a_{2}+b_{2}}{2}}{\frac{b_{1}+c_{1}}{2}-\frac{a_{1}+b_{1}}{2}}=\frac{c_{2}-a_{2}}{c_{1}-a_{1}}\) = slope \(\overline{T U}\); since slopes are equal, segments are parallel.

Slope \(\overline{S T}\)= \(\frac{\frac{b_{2}+c_{2}}{2}-\frac{c_{2}+d_{2}}{2}}{\frac{b_{1}+c_{1}}{2}-\frac{c_{1}+d_{1}}{2}}=\frac{b_{2}-d_{2}}{b_{1}-d_{1}}\) = slope \(\overline{U R}\); since slopes are equal, segments are parallel.

Question 9.
The Pythagorean theorem states that if three squares are drawn on the sides of a right triangle, then the area of the largest square equals the sum of the areas of the two remaining squares.

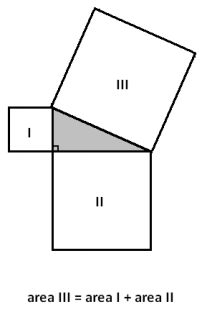
There must be a point P along the hypotenuse of the right triangle at which the large square is divided into two rectangles as shown, each with an area matching the area of one of the smaller squares.

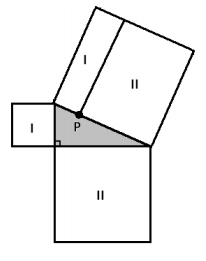
Consider a right triangle AOB situated on the coordinate plane with vertex A on the positive y – axis, O at the origin, and vertex B on the positive x – axis.

Suppose A has coordinates (0, a), B has coordinates (b, 0), and the length of the hypotenuse \(\overline{A B}\) is c.

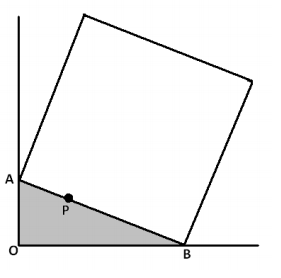
a. Find the coordinates of a point P on \(\overline{A B}\) such that \(\overline{O P}\) is perpendicular to \(\overline{A B}\).
Answer:
Equation of \(\overline{A B}\): y = –\(\frac{a}{b}\) x + a
Equation of \(\overline{O P}\): y = \(\frac{b}{a}\) x
P (\(\frac{a^{2} b}{a^{2}+b^{2}}\) ) , \(\frac{a b^{2}}{a^{2}+b^{2}}\) )

b. Show that for this point P we have \(\frac{AP}{PB}\) = \(\frac{a^{2}}{b^{2}}\).
Answer:

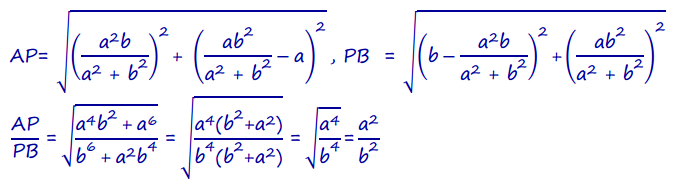
c. Show that if we draw from P a line perpendicular to \(\overline{A B}\), then that line divides the square with \(\overline{A B}\) as one of its sides into two rectangles, one of area a² and one of area b².
Answer:
Rectangle I: width = \(\frac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}}}\), height = \(\frac{a^{2}}{\sqrt{a^{2}+b^{2}}}\), area = \(\frac{\left(a^{4}+a^{2} b^{2}\right)}{a^{2}+b^{2}}\)

Rectangle II: width = \(\frac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}}}\), height = \(\frac{b^{2}}{\sqrt{a^{2}+b^{2}}}\), area = \(\frac{\left(a^{2} b^{2}+b^{4}\right)}{a^{2}+b^{2}}\)