Engage NY Eureka Math Geometry Module 4 Lesson 2 Answer Key
Eureka Math Geometry Module 4 Lesson 2 Example Answer Key
Example 1.
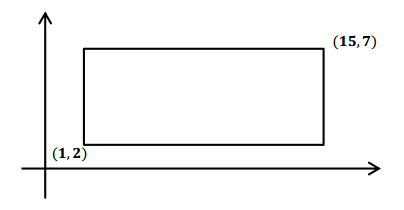
Answer:
→ Name three points inside the rectangular region.
Answers will vary. Possible answers include (2, 2), (5, 4), and (14, 6).
→ Name three points on the boundary of the rectangular region.
Answers will vary. Possible answers include (3, 2), (15, 6), and (7, 7).
→ What if we want to know all of the points in the region and on the boundary? How can I describe those points?
Let students brainstorm and do a 30 – second Quick Write; then, share ideas with the class before asking the following.
→ Can you say anything about the possible value of x?
The x – values are to the right of 1 but to the left of 15; the x – values are greater than or equal to 1; the x – values are less than or equal to 15; x ≥ 1 and x ≤ 15; 1 ≤ x ≤ 15.
→ Can you say anything about the possible value of y?
The y – values are above 2 but below 7; the y – values are greater than or equal to 2; the y – values are less than or equal to 7; y ≥ 2 and y ≤ 7; 2 ≤ y ≤ 7.
→ What can you say about the coordinates of points that lie on the left side of this rectangular region?
The points on the left border of this rectangle all have x – coordinates of 1. On the top side?
The points on the top border of this rectangle all have y – coordinates of 7.
→ The region is a rectangle. Let’s review the properties of a rectangle. (Have students share ideas on the board.)
All rectangles have opposite sides parallel, opposite sides congruent, 4 right angles, and diagonals congruent.
→ What is the length of a diagonal of the rectangular region?
The diagonal is approximately 14.9 units.
→ Does it matter which of the two diagonals you work with?
No, the diagonals of a rectangle are the same length.
→ Can you give the coordinates of a point within the rectangular region that lies on the diagonal that connects (1, 2) to (15, 7)?
There are an infinite number of points on the diagonal. Students may find the point lying in the middle by averaging the values and get (8, 4.5), or they could use the rise over run triangle and find other points such as (3.8, 3).
Example 2.
Draw the triangular region in the plane given by the triangle with vertices (0, 0), (1, 3), and (2, 1). Can we write a set of inequalities that describes this region?
Answer:
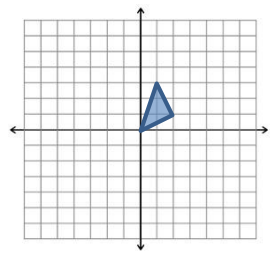
y ≤ 3x
y ≥ \(\frac{1}{2}\)x
y ≤ – 2x + 5
Eureka Math Geometry Module 4 Lesson 2 Exercise Answer Key
Opening Exercises
Graph each system of inequalities.
Answer:
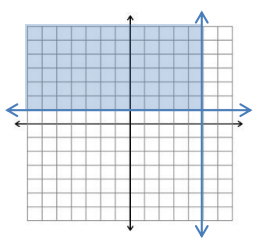
a. y ≥ 1
x ≤ 5
i. Is (1, 2) a solution? Explain.
Answer:
Yes, (1, 2) is inside the region.
ii. Is (1, 1) a solution? Explain.
Answer:
Yes, (1, 1) is on the border of the region and included in the region.
iii. The region is the intersection of how many half – planes? Explain how you know.
Answer:
It is the intersection of 2 half planes, x ≤ 5 and y ≥ 1. x ≤ 5 splits the plane in half at the vertical line x=5 and to the left. y ≥ 1 cuts the plane in half horizontally from the line y=1 and above.
Answer:
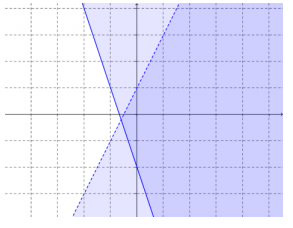
b. y < 2x + 1
y ≥ – 3x – 2
i. Is ( – 2, 4) in the solution set?
Answer:
No, it does not belong to the overlapping shaded region.
ii. Is (1, 3) in the solution set?
Answer:
No, (1, 3) is not in the solution set because it is on the boundary, but that boundary is not included.
iii. The region is the intersection of how many half – planes? Explain how you know.
Answer:
It is the intersection of 2 half planes and includes the portion of the line y<2x + 1 above the intersection, and the portion of the line y≥ – 3x – 2 below the intersection.
Exercises 1–3
Exercise 1.
Given the region shown to the right:
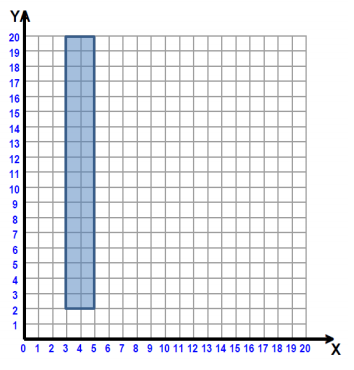
a. Name three points in the interior of the region.
Answer:
Answers will vary but could include (4, 3), (3.5, 7), and (4.5, 19).
b. Name three points on the boundary.
Answer:
Answers will vary but could include (4, 2), (3, 15), and (5, 18).
c. Describe the coordinates of the points in the region.
Answer:
All x – coordinates are greater than or equal to 3 and less than or equal to 5, and all y – coordinates are greater than or equal to 2 and less than or equal to 20.
d. Write the inequality describing the x – values.
Answer:
x ≥ 3, x ≤ 5 or 3 ≤ x ≤ 5
e. Write the inequality describing the y – values.
Answer:
y ≥ 2, y ≤ 20 or 2 ≤ y ≤ 20
f. Write this as a system of equations.
Answer:
{(x, y)│3 ≤ x ≤ 5, 2 ≤ y ≤ 20}
g. Will the lines x=4 and y=1 pass through the region? Draw them.
Answer:
x=4 vertically cuts the region in half. y=1 is below the region and horizontal.
Exercise 2.
Given the region that continues unbound to the right as shown to the right:
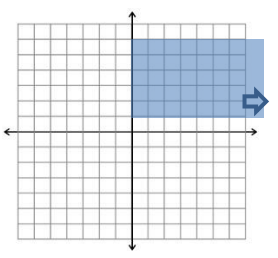
a. Name three points in the region.
Answer:
Answers will vary but could include (2, 2), (4, 3), and (5, 4).
b. Describe in words the points in the region.
Answer:
The region is above y=1 and below y=5. It starts at x=0 and continues to the right without bound.
c. Write the system of inequalities that describe the region.
Answer:
{(x, y)│x ≥ 0, 1 ≤ y ≤ 5}
d. Name a horizontal line that passes through the region.
Answer:
Answers will vary but may include y=4.
Exercise 3.
Given the region that continues down without bound as shown to the right:
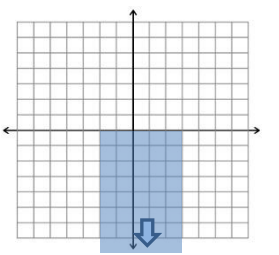
a. Describe the region in words.
Answer:
The region is to the right of x= – 2 and to the left of x=3. It starts at y=0 and continues down without bound.
b. Write the system of inequalities that describe the region.
Answer:
{(x, y)│ – 2 ≤ x ≤ 3, y ≤ 0}
c. Name a vertical line that passes through the region.
Answer:
Answers will vary but may include x= – 1.
Exercises 4–5
Exercise 4.
Given the triangular region shown, describe this region with a system of inequalities.
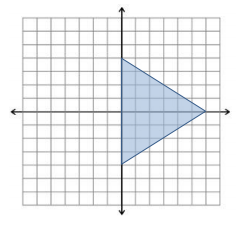
Answer:
x ≥ 0
y ≥ \(\frac{2}{3}\)x – 4
y ≤ – \(\frac{2}{3}\) x + 4
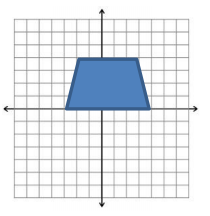
Exercise 5.
Given the trapezoid with vertices ( – 2, 0), ( – 1, 4), (1, 4), and (2, 0), describe this region with a system of inequalities.
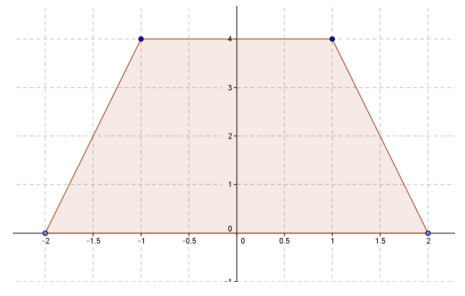
Answer:
y ≥ 0
y ≤ 4
y ≥ 4x + 8
y ≤ – 4x + 8
Eureka Math Geometry Module 4 Lesson 2 Problem Set Answer Key
Question 1.
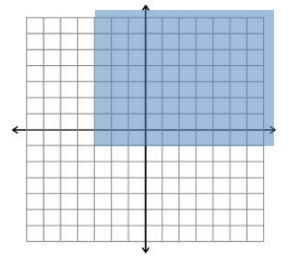
Given the region shown:
Answer:
a. How many half – planes intersect to form this region?
Answer:
2
b. Name three points on the boundary of the region.
Answer:
( – 1, – 1), ( – 3, 4), and (5, – 1)
c. Describe the region in words.
Answer:
The region is above and includes y= – 1, is to the right of and includes x= – 3, and extends without bound to the top and right.
Question 2.
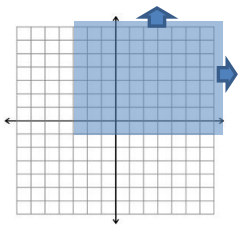
Region T is shown to the right.
a. Write the coordinates of the vertices.
Answer:
( – 1, – 4), ( – 1, 6), (3, 6), and (3, – 4)
b. Write an inequality that describes the region.
Answer:
{(x, y)│ – 1 ≤ x ≤ 3, – 4 ≤ y ≤ 6}
c. What is the length of the diagonals?
Answer:
The diagonal is approximately 10.8 units long.
d. Give the coordinates of a point that is both in the region and on one of the diagonals.
Answer:
Answers will vary. (1, 1) lies on the diagonal and in the interior of region T.
Question 3.
Jack wants to plant a garden in his backyard. His yard is 120 feet wide and 80 feet deep. He wants to plant a garden that is 20 feet by 30 feet.
a. Set up a grid for the backyard, and place the garden on the grid. Explain why you placed your garden in its place on the grid.
Answer:
Answers will vary, but the backyard should be on the grid with length 120 feet in the x – direction and 80 feet in the y – direction, or this can be set up in the other direction with 80 feet in the x – direction and 120 feet in the y – direction. The garden should form a rectangle somewhere on the grid.
b. Write a system of inequalities to describe the garden.
Answer:
Answers will vary.
c. Write the equation of three lines that would go through the region that he could plant on, and explain your choices.
Answer:
Answers will vary.
Question 4.
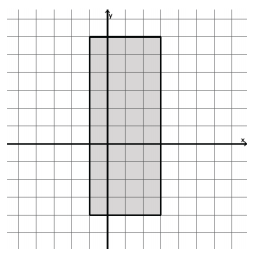
Given the trapezoidal region shown to the right:
a. Write the system of inequalities describing the region.
Answer:
y ≤ 4x + 12
y ≤ 4
y ≤ – 4x + 16
y ≥ 0
b. Translate the region to the right 3 units and down 2 units. Write the system of inequalities describing the translated region.
Answer:
y ≤ 4x – 2
y ≤ 2
y ≤ – 4x + 26
y ≥ – 2
Challenge Problems:
Question 5.
Given the triangular region shown with vertices A( – 2, – 1), B(4, 5), and C(5, – 1):
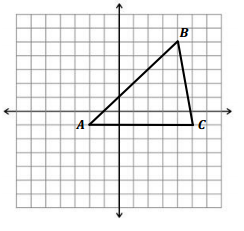
a. Describe the systems of inequalities that describe the region enclosed by the triangle.
Answer:
y ≤ x + 1
y ≤ – 6x + 29
y ≥ – 1
b. Rotate the region 90° counterclockwise about Point A. How will this change the coordinates of the vertices?
Answer:
A( – 2, – 1), B( – 8, 5), and C( – 2, 6)
c. Write the system of inequalities that describe the region enclosed in the rotated triangle.
Answer:
y ≥ – x – 3
y ≤ \(\frac{1}{6}\)x + \(\frac{19}{3}\)
x ≤ – 2
Question 6.
Write a system of inequalities for the region shown.
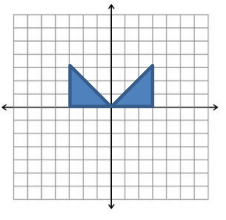
Answer:
y ≤ |x|
y ≥ 0
|x| ≤ 3
Eureka Math Geometry Module 4 Lesson 2 Exit Ticket Answer Key
Question 1.
Given the region shown:
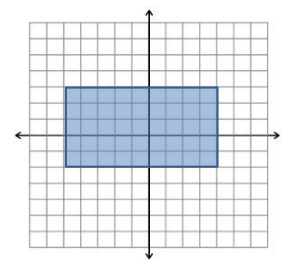
a. Name three points in the region.
Answer:
Answers will vary but may include (0, 0), ( – 2, 3), (4, – 1).
b. Identify the coordinates of the four vertices.
Answer:
( – 4, – 2), ( – 4, 3), (5, 3), and (5, – 2)
c. Write the system of inequalities describing this region.
Answer:
{(x, y)│ – 4 ≤ x ≤ 5, – 2 ≤ y ≤ 3}