Eureka Math Geometry Module 3 Lesson 5 Answer Key

Engage NY Eureka Math Geometry Module 3 Lesson 5 Answer Key

Eureka Math Geometry Module 3 Lesson 5 Exercise Answer Key

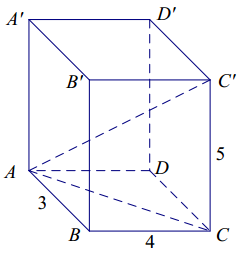
The following three-dimensional right rectangular prism has dimensions 3 × 4 × 5.
Determine the length of \(\overline{A C^{\prime}}\). Show a full solution.
Answer:
By the Pythagorean theorem, the length of \(\overline{A C}\): is 5 units long. So, triangle ACC’ is a right triangle whose legs both have length 5. In other words, it is 45-45-90 right triangle. So, \(\overline{A C^{\prime}}\) has length 5√2.

Eureka Math Geometry Module 3 Lesson 5 Problem Set Answer Key

Question 1.
Indicate whether each statement is always true (A), sometimes true (S). or never true (N).
a. If two lines are perpendicular to the same plane, the lines are parallel.
Answer:
A

b. Two planes can intersect in a point.
Answer:
N

c. Two lines parallel to the same plane are perpendicular to each other.
Answer:
S

d. If a line meets a plane in one point, then it must pass through the plane.
Answer:
A

e. Skew lines can lie in the same plane.
Answer:
N

f. If two lines are parallel to the same plane, the lines are parallel.
Answer:
S

g. If two planes are parallel to the same line, they are parallel to each other.
Answer:
A

h. If two lines do not intersect, they are parallel.
Answer:
S

Question 2.
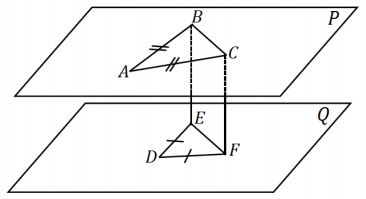
Consider the right hexagonal prism whose bases are regular hexagonal regions. The top and the bottom hexagonal regions are called the base faces, and the side rectangular regions are called the lateral faces.

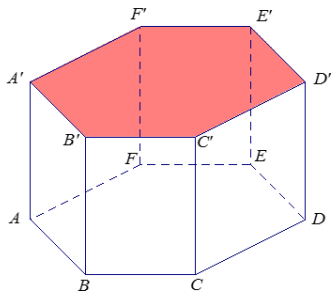
a. List a plane that Is parallel to plane C’D’E’.
Students may define planes using different points. A correct sample response is shown:
Answer:
Plane ABC

b. List all planes shown that are not parallel to plane CDD’.
Answer:
Students may define planes using different points. A correct sample response is shown:
Planes ABB’, BBC’, DEE’, EFF’, FAA’, A’B’C’, and ABC.

c. Name a line perpendicular to plane ABC.
Students may define planes using different points. A correct sample response is shown:
Answer:

d. Explain why AA’ = CC’.
Answer:
The bases of the right prism are parallel planes, which means that the lateral faces are perpendicular to the bases; hence, the lines contained in the lateral faces are perpendicular to the base planes. Any two line segments connecting parallel planes have the same length if they are each perpendicular to one (and hence both) of the planes.

e. Is parallel to ? Explain.
Answer:
Yes, and lie in the same base plane and are opposite sides of a regular hexagon.

f. Is parallel to ? Explain.
Answer:
No, the lines do not intersect; however, they are not in the same plane and are, therefore, skew.

g. Is parallel to ? Explain.
Answer:
is parallel to since the lines contain opposite sides of a parallelogram (or rectangle). Together with the result of part (e), if two lines are parallel to the same line, then those two lines are also parallel. Even though the lines do not appear to be on the same plane in the given figure, there is a plane that is determined by points A, B, E’, and D’.

h. If \(\overline{B C^{\prime}}\) and \(\overline{\boldsymbol{C}^{\prime} \boldsymbol{F}^{\prime}}\) are perpendicular, then is perpendicular to plane C’A’F’? Explain.
Answer:
No, for a line to be perpendicular to a plane, it must be perpendicular to two (and thus all) lines in the plane. The given information only provides one pair of perpendicular lines.

i. One of the following statements is false. Identify which statement is false, and explain why.

Answer:

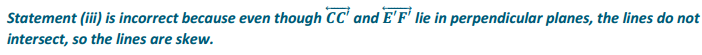
Question 3.
In the following figure, ∆ ABC is in plane P, ∆ DEF is in plane Q, and BCFE is a rectangle. Which of the following statements are true?

a. \(\overline{B E}\) is perpendicular to plane Q.
Answer:
True

b. BF = CE
Answer:
True

c. Plane P is parallel to plane Q.
Answer:
True

d. ∆ ABC ≅ ∆ DEF
Answer:
False

e. AE = AF
Answer:
True

Question 4.
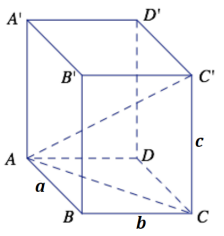
Challenge: The following three-dimensional right rectangular prism has dimensions a × b × c. Determine the length of \(\overline{A C^{\prime}}\).

Answer:
By the Pythagorean theorem, the length of \(\overline{A C}\) is \(\sqrt{a^{2}+b^{2}}\) units long.
∆ ACC’ is a right triangle with AC = \(\sqrt{a^{2}+b^{2}}\) and CC’ = 5.
Then,
\(\overline{A C^{\prime}}\) = \(\sqrt{\left(\sqrt{a^{2}+b^{2}}\right)^{2}+c^{2}}\)
or
\(\overline{A C^{\prime}}\) = \(\sqrt{a^{2}+b^{2}+c^{2}}\)

Question 5.
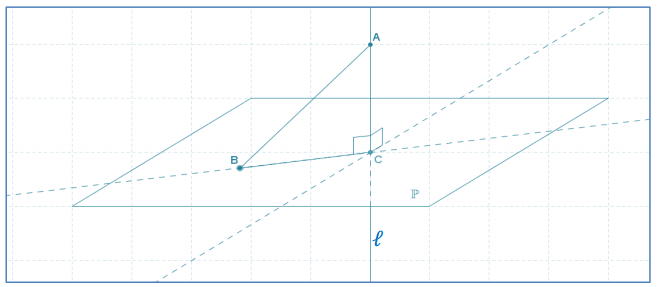
A line l is perpendicular to plane P. The line and plane meet at point C. If A is a point on l different from C, and B is a point on P different from C, show that AC < AB.
Answer:
Consider ∆ ABC. Since F is perpendicular to P, ∠ACB is a right angle no matter where B and C lie on the plane. So, \(\overline{A B}\) is the hypotenuse of a right triangle, and \(\overline{A C}\) is a leg of the right triangle. By the Pythagorean theorem, the length of either leg of a right triangle is less than the length of the hypotenuse. Thus, AC < AB.

Question 6.
Given two distinct parallel planes P and R, in P with EF = 5, point G in R, m∠GEF = 90°, and m∠EFG = 60°, find the minimum and maximum distances between planes P and R, and explain why the actual distance is unknown.
Answer:

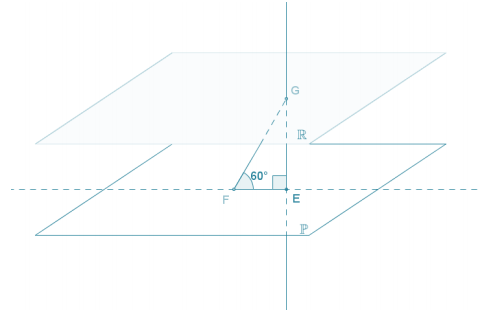
Triangle EFG is a 30-60-90 triangle with its short leg of length 5 units. The length of the longer leg must be √3, or approximately 8.7. The maximum distance between the planes is approximately 8.7.

If plane EFG is perpendicular to plane P, then the distance between the planes is equal to the length of the longer leg of the right triangle. If plane EFG is not perpendicular to plane P (and plane R), then the distance between the planes must be less than 5√3. Furthermore, the distance between the distinct parallel planes must be greater than zero, or the planes would coincide.

The actual distance is unknown because the plane determined by points E, F, and G may or may not be perpendicular to planes P and R.

Question 7.
The diagram below shows a right rectangular prism determined by vertices A, B, C, D, E, F, G, and H. Square ABCD has sides with length 5, and AE = 9. Find DF.

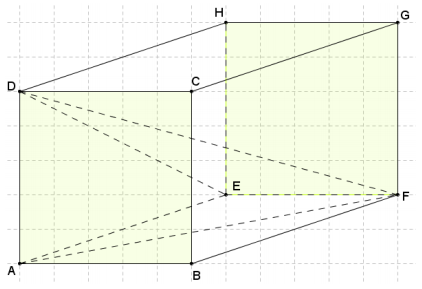
Answer:
The adjacent faces on a right rectangular prism are perpendicular, so angle AEF must then be a right angle.
Using the Pythagorean theorem:
AF² = AE² + EF²
AF² = 9² + 5²
AF² = 81 + 25
AF = √106

\(\overline{D A}\) is perpendicular fo plane AEFB since it Is perpendicular to both \(\overline{A B}\) and \(\overline{A E}\); therefore, It is perpendicular fo all lines in plane AEFB. Then, triangle AFD is a right triangle with legs of length AD = 5 and AF = √106.
Using the Pythagorean theorem:
DF² = DA² + AF²
DF² = 5² + (√106)²
DF² = 25 + 106
DF² = 131
DF = √131 ≈ 11.4
The distance DF is approximately 11.4.

Eureka Math Geometry Module 3 Lesson 5 Exit Ticket Answer Key

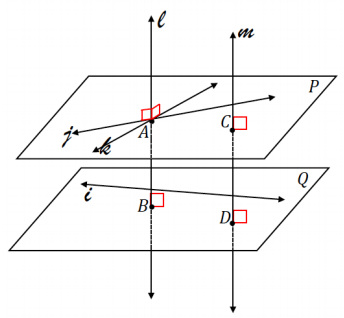
Question 1.
What can be concluded about the relationship between line l and plane P? Why?
Answer:
Since line l is perpendicular to two lines that lie in plane P, line l must be perpendicular to plane P.

Question 2.
What can be concluded about the relationship between planes P and Q? Why?
Answer:
Since line m is perpendicular to both planes P and Q, planes P and Q must be parallel to each other.

Question 3.
What can be concluded about the relationship between lines l and m? Why?
Answer:
Since lines l and m ore both perpendicular to both planes P and Q, lines l and m must be parallel to each other.

Question 4.
What can be concluded about \(\overline{A B}\) and \(\overline{C D}\)?
Answer:
AR = CD

Question 5.
Line j lies in plane P, and line i lies In plane Q. What can be concluded about the relationship between lines i and j?
Answer:
Lines i and j are skew lines.

Eureka Math Geometry Module 3 Lesson 5 Exploratory Challenge Answer Key

Answer: