Engage NY Eureka Math Geometry Module 3 Lesson 4 Answer Key
Eureka Math Geometry Module 3 Lesson 4 Example Answer Key
a. Begin to approximate the area of a circle using inscribed polygons.
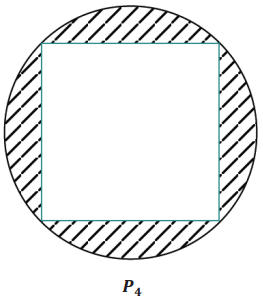
How well does a square approximate the area of a disk? Create a sketch of P4 (a regular polygon with 4 sides, a square) in the following circle. Shade in the area of the disk that is not included in P4.

Answer:
b. Next, create a sketch of P8 in the following circle.
Answer:
Guide students in how to locate all the vertices of P8 by resketching a square and then marking a point equally spaced between each pair of vertices; join the vertices to create a sketch of regular octagon P8.
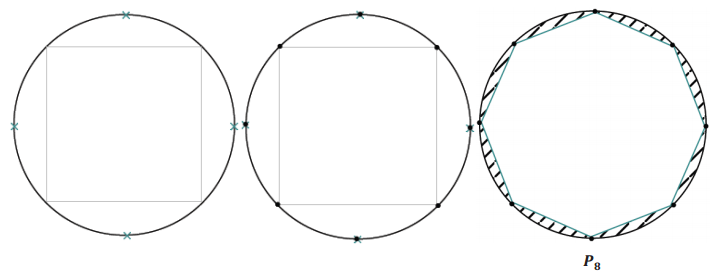
c. Indicate which polygon has a greater area.
Area(P4) ________ Area (P8)
Answer:
Area(P4) < Area (P8)
d. Will the area of inscribed regular polygon P16 be greater or less than the area of P8? Which is a better approximation of the area of the disk?
Answer:
Area(P8) < Area(P16); the area of P16 is a better approximation of the area of the disk.
Share a sketch of the following portion of the transition between P8 and P16 in a disk with students. Ask students why the area of P16 is a better approximation of the area of the circle.
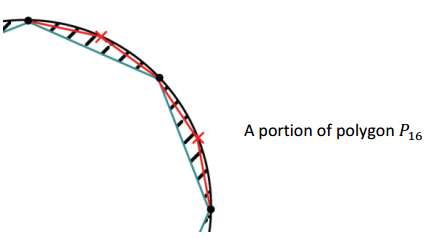
e. We noticed that the area of P4 was less than the area of P8 and that the area of P8 was less than the area of
P16. In other words, Area(Pn) ________ Area(P2n). Why is this true?
Answer:
Area(Pn) < Area(P2n).
We are using the n-polygon to create the 2n-polygon. When we draw the segments that join each new vertex in between a pair of existing vertices, the resulting 2n-polygon has a greater area than that of the n- polygon.
f. Now we will approximate the area of a disk using circumscribed (outer) polygons.
Now circumscribe, or draw a square on the outside of, the following circle such that each side of the square intersects the circle at one point. We will denote each of our outer polygons with prime notation; we are sketching P’4 here.

Answer:
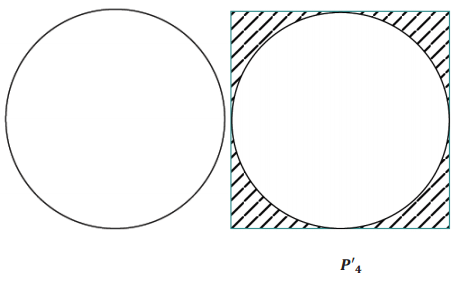
g. Create a sketch of P’8

Answer:
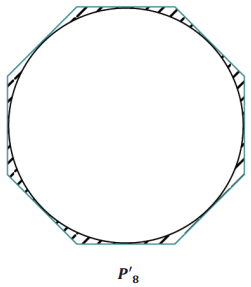
h. Indicate which polygon has a greater area.
Area(P’4) ________ Area(P’8)
Answer:
Area(P’4) > Area(P’8)
I. Which is a better approximation of the area of the circle, P’4 or P’8? Explain why.
Answer:
P’8 is a better approximation of the area of the circle relative to P’4 because it Is closer in shape to the circle than P’4.
j. How will Area(P’n) compare to Area(P’2n)? Explain.
Answer:
Area(P’n) > Area(P’2n). P’2n, can be created by chipping off its vertices; therefore, the area of P’2n will always be less than the area of P’n,.
Eureka Math Geometry Module 3 Lesson 4 Opening Exercise Answer Key
The following image is of a regular hexagon inscribed in circle C with radius r. Find a formula for the area of the hexagon in terms of the length of a side, s, and the distance from the center to a side.
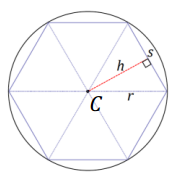
Answer:
The area formula for each of the congruent triangles is \(\frac{1}{2}\) sh. The area of the entire regular hexagon, which consists of 6 such triangles, is represented by the formula 3sh.
Eureka Math Geometry Module 3 Lesson 4 Problem Set Answer Key
Question 1.
Describe a method for obtaining closer approximations of the area of a circle. Draw a diagram to aid in your explanation.
Answer:
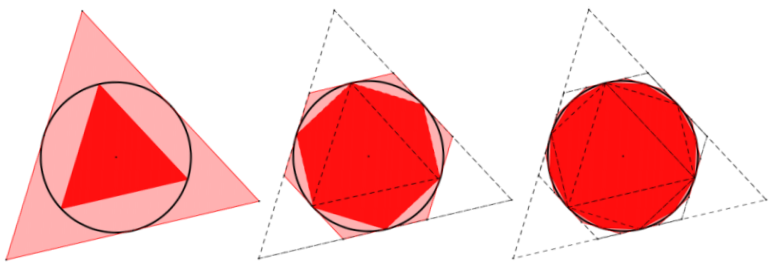
The area of a disk can be approximated to a greater degree of accuracy by squeezing the circle between regular polygons whose areas closely resemble that of the circle. The diagrams below start on the left with inscribed and circumscribed equilateral triangles. The areas of the triangles appear to be quite different, but the disk appears to be somewhere between the area of the larger triangle and the smaller triangle.
Next, double the number of sides of the inscribed and circumscribed polygons, forming inscribed and circumscribed regular hexagons, whose areas are closer to that of the disk (see the center diagram). Continue the process to create inscribed and circumscribed regular dodecagons, whose areas appear even closer yet to that of the disk (see the right diagram). The process can be performed on the dodecagons to produce regular 24-gons, then regular 48-gons, etc. As the number of sides of the regular inscribed and circumscribed polygons increases, the polygonal regions more closely approach the area of the disk, squeezing the area of the disk between them.
Question 2.
What is the radius of a circle whose circumference is π?
Answer:
The radius is \(\frac{1}{2}\).
Question 3.
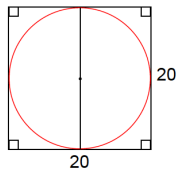
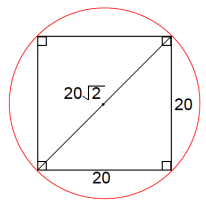
The side of a square is 20 cm long. What is the circumference of the circle when …
a. The circle is inscribed within the square?
Answer:
The diameter of the circle must be 20, so the circumference is 20π.
b. The square is inscribed within the circle?
Answer:
The diameter of the circle must be 20√2, so the circumference is 20π√2.
Question 4.
The circumference of circle C1 is 9 cm, and the circumference of C2 is 2π cm. What is the value of the ratio of the areas of C1 to C2?
Answer:
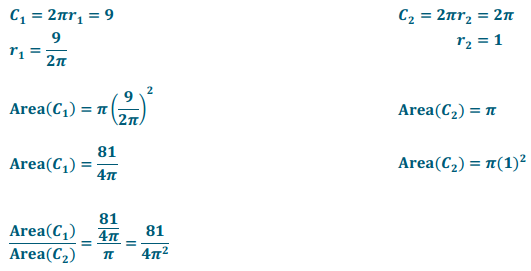
Question 5.
The circumference of a circle and the perimeter of a square are each 50 cm. Which figure has the greater area?
Answer:

Question 6.
Let us define π to be the circumference of a circle whose diameter is 1.
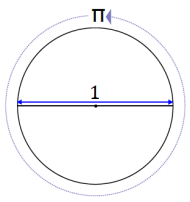
We are going to show why the circumference of a circle has the formula 2πr. Circle C1 below has a diameter of d = 1, and circle C2 has a diameter of d = 2r.
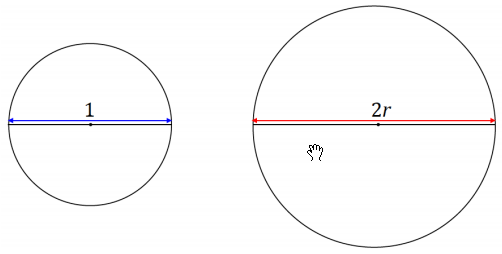
a. All circles are similar (proved in Module 2). What scale factor of the similarity transformation takes C1 to C2?
Answer:
A scale factor of 2r
b. Since the circumference of a circle is a one-dimensional measurement, the value of the ratio of two circumferences is equal to the value of the ratio of their respective diameters. Rewrite the following equation by filling in the appropriate values for the diameters of C1 and C2:
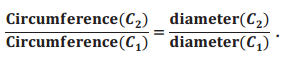
Answer:
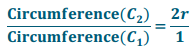
c. Since we have defined π to be the circumference of a circle whose diameter is 1, rewrite the above equation using this definition for C1.
Answer:
\(\frac{\text { Circumference }\left(C_{2}\right)}{\pi}=\frac{2 r}{1}\)
d. Rewrite the equation to show a formula for the circumference of C2.
Answer:
Circumference(C2) = 2πr
e. What can we conclude?
Answer:
Since C2 is an arbitrary circle, we have shown that the circumference of any circle is 2πr.
Question 7.
a. Approximate the area of a disk of radius 1 using an inscribed regular hexagon. What is the percent error of the approximation? (Remember that percent error is the absolute error as a percent of the exact measurement.)
Answer:
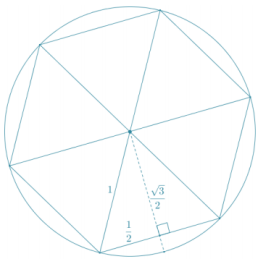
The inscribed regular hexagon is divided into six equilateral triangles with side lengths equal to the radius of the circle, 1. By drawing the altitude of an equilateral triangle, it is divided into two 3 0-60-90 right triangles. By the Pythagorean theorem, the altitude, h, has length \(\frac{\sqrt{3}}{2}\).
The area of the regular hexagon:
Area = \(\frac{1}{2}\) ph
Area = \(\frac{1}{2}\) (6 · 1) · \(\frac{\sqrt{3}}{2}\)
Area = \(\frac{3}{2}\)√3 ≈ 2.60
Percent Error = \(\frac{|x-a|}{a}\)
Percent Error = \(\frac{\pi-\frac{3}{2} \sqrt{3}}{\pi}\) ≈ 17.3%
The estimated area of the disk using the inscribed regular hexagon is approximately 2.60 square units with a percent error of approximately 17.3%.
b. Approximate the area of a circle of radius 1 using a circumscribed regular hexagon. What is the percent error of the approximation?
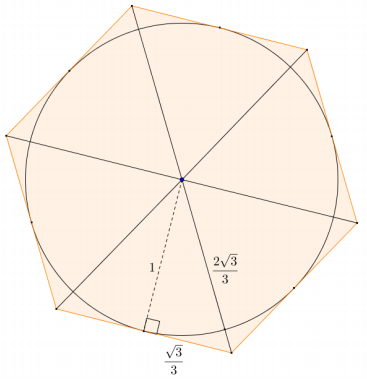
Answer:
The circumscribed regular hexagon can be divided into six equilateral triangles, each having an altitude equal in length to the radius of the circle. By the Pythagorean theorem, the sides of the equilateral triangles are \(\frac{2 \sqrt{3}}{3}\).
Area = \(\frac{1}{2}\)ph
Area = \(\frac{1}{2}\) (6 · \(\frac{2 \sqrt{3}}{3}\)) · 1
Area= 2√3 ≈ 3.46
Percent Error = \(\frac{|x-a|}{a}\)
Percent Error = \(\frac{2 \sqrt{3}-\pi}{\pi}\) ≈ 10.3%
The estimated area of the disk using the circumscribed regular hexagon is approximately 3.46 square units with a percent error of approximately 10.3%.
c. Find the average of the approximations for the area of a circle of radius 1 using inscribed and circumscribed regular hexagons. What is the percent error of the average approximation?
Answer;
Let Avv, represent the average approximation for the area of the disk, and let Ax be the exact area of the disk using the area formula.

Question 8.
A regular polygon with n sides each of length s is inscribed in a circle of radius r. The distance h from the center of the circle to one of the sides of the polygon is over 98% of the radius. If the area of the polygonal region is 10, what can you say about the area of the circumscribed regular polygon with n sides?
Answer:
The circumscribed polygon has area \(\left(\frac{r}{h}\right)^{2}\)2 (10).
Since 0. 98r < h < r, by inversion \(\frac{1}{0.98 r}\) > \(\frac{1}{h}\) > \(\frac{1}{r}\).
By multiplying by r, \(\frac{r}{0.98 r}\) = \(\frac{1}{0.98 r}\) > \(\frac{\boldsymbol{r}}{\boldsymbol{h}}\) > 1.
The area of the circumscribed polygon is \(\left(\frac{r}{h}\right)^{2}\) 10 < \(\left(\frac{1}{0.98}\right)^{2}\) 10 < 10.42.
The area of the circumscribed polygon is less than 10.42 square units.
Eureka Math Geometry Module 3 Lesson 4 Exit Ticket Answer Key
Question 1.
Approximate the area of a disk of radius 2 using an inscribed regular hexagon.
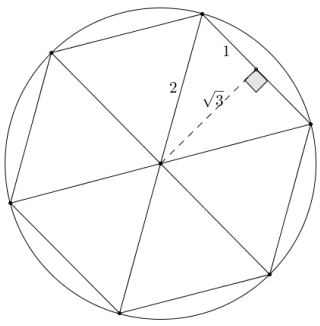
Answer:
The interior of a regular hexagon can be divided into 6 equilateral triangles, each of which can be split into two 30-60-90 triangles by drawing on altitude. Using the relationships of the sides in a 30-60-90 triangle, the height of each triangle is
Area = \(\frac{1}{2}\)ph
Area = \(\frac{1}{2}\)(2 · 6) · √3
Area = 6√3
The area of the inscribed regular hexagon is 6√3.
Question 2.
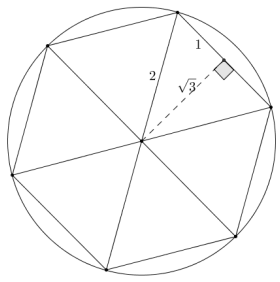
Approximate the area of a disk of radius 2 using a circumscribed regular hexagon.
Answer:
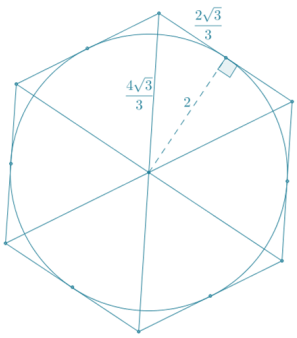
Using the same reasoning for the interior of the hexagon, the height of the equilateral triangles contained in the hexagon is 2, while the lengths of their sides are \(\frac{4 \sqrt{3}}{3}\).
Area = \(\frac{1}{2}\)ph
Area = \(\frac{1}{2}\)(\(\frac{4 \sqrt{3}}{3}\) · 6) · 2
Area = (4√3 · 2)
Area = 8√3
The area of the circumscribed regular hexagon is 8√3.
Question 3.
Based on the areas of the inscribed and circumscribed hexagons, what is an approximate area of the given disk? What is the area of the disk by the area formula, and how does your approximation compare?
Answer:
Average approximate area: Area formula:
A = \(\frac{1}{2}\)(6√3 + 8√3) A = π(2)2
A = \(\frac{1}{2}\)(14√3) A = π(4)
A = 7√3 ≈ 12.12 A = 4π ≈ 12.57
The approximated area is close to the actual area but slightly less.