Engage NY Eureka Math Geometry Module 3 Lesson 6 Answer Key
Eureka Math Geometry Module 3 Lesson 6 Opening Exercise Answer Key
Sketch a right rectangular prism.
Answer:
Sketches may vary. Note whether students use dotted lines to show hidden edges, and ask students with sketches showing no hidden edges to compare images with students who do have hidden edges shown.
RIGHT RECTANGULAR PRISM: Let E and E’ be two parallel planes. Let B be a rectangular region1 in the plane E. At each point P of B, consider \(\overline{P P^{\prime}}\) perpendicular to E, joining P to a point P’ of the plane E’. The union of all these segments is called a right rectangular prism. ____________
1(Fill in the blank.) A rectangular region is the union of a rectangle and ____________.
Answer:
1(Fill in the blank.) A rectangular region is the union of a rectangle and its interior.
Eureka Math Geometry Module 3 Lesson 6 Exercise Answer Key
a.
Answer:

b.
Answer:
c.
Answer:

d.
Answer:

Eureka Math Geometry Module 3 Lesson 6 Problem Set Answer Key
Question 1.
Complete each statement below by filling in the missing term(s).
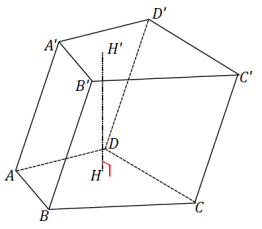
a. The following prism Is called a(n) _______ prism.
Answer:
Oblique
b. If \(\overline{A A^{\prime}}\) were perpendicular to the plane of the base, then the prism would be called a(n) _______ prism.
Answer:
Right
c. The regions ABCD and A’B’C’D’ are called the _______ of the prism.
Answer:
Bases
d. \(\overline{A A^{\prime}}\) is called a(n) _______.
Answer:
Edge
e. Parallelogram region BB’C’C is one of four _______ _______.
Answer:
Lateral faces
Question 2.
The following right prism has trapezoidal base regions; it is a right trapezoidal prism. The lengths of the parallel edges of the base are 5 and 8, and the nonparallel edges are 4 and 6; the height of the trapezoid is 3. 7. The lateral edge length DH is 10. Find the surface area of the prism.
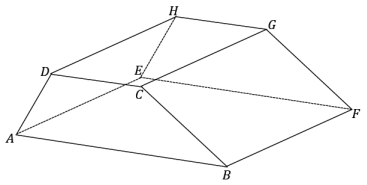
Answer:
Area(bases) = 2 × \(\left(\frac{5+8}{2}\right)\) (3.7) = 48.1
Area(DEGH) = 5(10) = 50
Area(BCGF) = 6(10) = 60
Area(ABFE) = 8(10) = 80
Area(ADHE) = 4(10) = 40
Total Surface Area = 48.1 + 50 + 60 +80 + 40 = 278.1
Question 3.
The base of the following right cylinder has a circumference of 5ff and a lateral edge of 8. What is the radius of the base? What is the lateral area of the right cylinder?
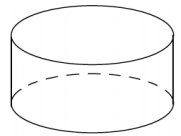
Answer:
The radius of the base is 2.5.
The lateral area is 5π(8) or 40π.
Question 4.
The following right general cylinder has a lateral edge of length 8, and the perimeter of its base is 27. What is the lateral area of the right general cylinder?
Answer:
The lateral area is 2 7(8) or 216.
Question 5.
A right prism has base area 5 and volume 30. Find the prism’s height, h.
Answer:
Volume = (area of base) × (height)
30 = (5)h
6 = h
The height of the prism is 6.
Question 6.
Sketch the figures formed if the rectangular regions are rotated around the provided axis.
a.

Answer:
b.
Answer:
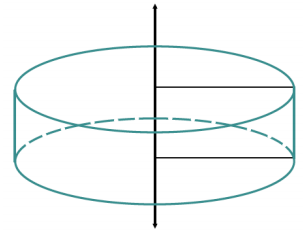
Question 7.
A cross-section Is taken parallel to the bases of a general cylinder and has an area of 18. If the height of the cylinder is h, what is the volume of the cylinder? Explain your reasoning.
Answer:
If the cross-section is parallel to the bases of the cylinder, then it is congruent to the bases; thus, the area of the base of the cylinder is 18. The volume of a general cylinder is the product of the area of the cylinder’s base times the height of the cylinder, so the volume of the general cylinder is 18h.
Question 8.
A general cylinder has a volume of 144. What Is one possible set of dimensions of the base and height of the cylinder if all cross-sections parallel to its bases are…
a. Rectangles?
Answer:
Answers vary.
Volume = (Area of base) × (height)
Volume = 144
Volume = (12)(12)
Volume = (4 · 3)(12)
The base of the cylinder (rectangular prism) could be 4 × 3, and the cylinder could have a height of 12.
b. Right triangles?
Answer:
Answers vary.
Volume = (area of base) × (height)
Volume = 144
Volume = (12)(12)
Volume = \(\frac{1}{2}\)(6 · 4)(12)
The base of the cylinder (triangular prism) could be a right triangle with legs of length 6 and 4, and the cylinder could have a height of 12.
c. Circles?
Answer:
Answers vary.
Volume = (area of base) × (height)
Volume = 144
Volume = (12)(12)
Volume = \(\left(\pi\left(\sqrt{\frac{12}{\pi}}\right)^{2}\right)\) × (12)
The base of the cylinder (circular cylinder) could have a radius of \(\sqrt{\frac{12}{\pi}}\), and the cylinder could have a height of 12.
Question 9.
A general hexagonal prism is given. If P is a plane that is parallel to the planes containing the base faces of the prism, how does P meet the prism?
Answer:
If P is between the planes containing the base faces, then P meets the prism in a hexagonal region that is congruent to the bases of the prism; otherwise, P does not meet the prism.
Question 10.
Two right prisms have similar bases. The first prism has height 5 and volume 100. A side on the base of the first prism has length 2, and the corresponding side on the base of the second prism has length 3. If the height of the second prism is 6, what is its volume?
Answer:
The scale factor of the base of the second prism is \(\frac{3}{2}\), so its area is \(\left(\frac{3}{2}\right)^{2}\), the area of the base of the first prism.
Volume = (Area of base) × (height)
100 = (Area of base) × (5)
Area of base = 20
The area of the base of the first prism is 20.
The area of the base of the second prism is then \(\left(\frac{3}{2}\right)^{2}\) (20), or 45.
Volume = (Area of base) × (height)
Volume = (45) × (6)
Volume = 270
The volume of the second prism is 270.
Question 11.
A tank is the shape of a right rectangular prism with base 2 ft. × 2 ft. and height 8 ft. The tank is filled with water to a depth of 6 ft. A person of height 6 ft. jumps in and stands on the bottom. About how many inches will the water be over the person’s head? Make reasonable assumptions.
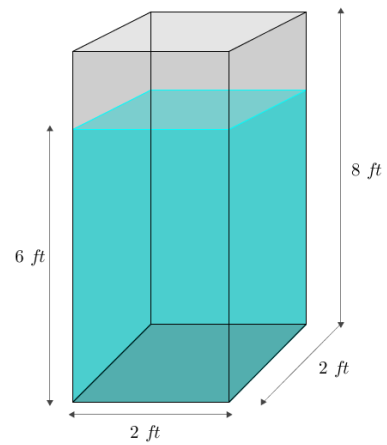
Answer:
Model the human as a right cylinder with height 6 ft. and base area \(\frac{1}{2}\) ft2. The volume of the human is then 3 ft3.
The depth of the water will be increased as the human displaces a volume of 3 ft3 of the water in the tank.
Let x represent the increase in depth of the water In feet.
Volume = (area of base) × (height)
3 ft3 = (4 ft2)(x)
\(\frac{3}{4}\)ft. = x
The water will rise by \(\frac{3}{4}\)ft. or 9 in., so the water will be approximately 9 in. over the human’s head.
Eureka Math Geometry Module 3 Lesson 6 Exit Ticket Answer Key
Question 1.
Is this a cylinder? Explain why or why not.
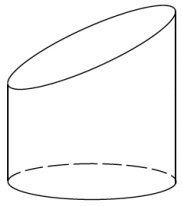
Answer:
The figure is not a cylinder because the bases are not parallel to each other.
Question 2.
For each of the following cross-sections, sketch the figure from which the cross-section was taken.
a.
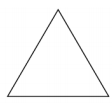
Answer:
b.
Answer:
Eureka Math Geometry Module 3 Lesson 6 Extension Answer Key
Extension
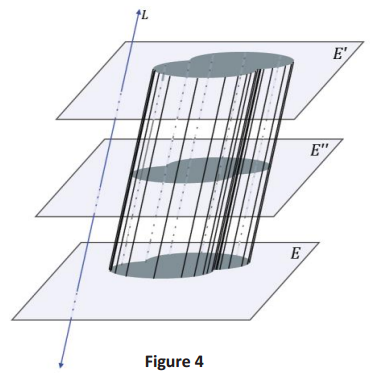
Answer:
→ They look like they are congruent.
→ Let us make the claim that all cross-sections of a general cylinder are congruent to the base. How can we show this to be true?
Allow students time to discuss with a partner how they could demonstrate this (i.e., a rough argument). How can they use what they know about the base regions being congruent to show that a cross-section is congruent to its respective base? Review the following argument after students have attempted the informal proof and shared their ideas:
→ Take a plane E” between E and E’ so that it is parallel to both.
→ The top portion of the cylinder is another cylinder and, hence, has congruent bases.
→ Thus, the cross-section lying in E” is congruent to both of the bases.
Consider modeling this idea using a deck of playing cards or a stack of coins. Is a cross-section of either group, whether stacked perpendicularly or skewed, congruent to a base?
For triangular prisms, the argument can be made more precise.
→ How have we determined whether two triangles are congruent or not in the past? What do we know about the parts of each of the triangles in the image, and what more do we need to know?
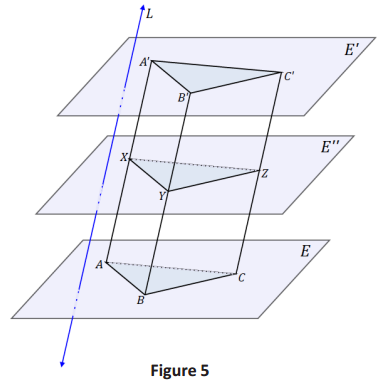
Answer:
Review the following argument after students have attempted the informal proof and shared their ideas:
→ As we know from earlier in the lesson, a prism is the totality of all segments PP’ parallel to line L from each point P from the base region joining P to a point P’ of the plane E’.
→ Points X, Y, and Z are the points where E” intersects \(\overline{A A^{\prime}}\), \(\overline{B B^{\prime}}\), and \(\overline{C C^{\prime}}\).
Then, \(\overline{A X}\) || \(\overline{B Y}\) because both segments are parallel to line L.
Also, \(\overline{A B}\) Il \(\overline{X Y}\) since lateral face ABB’A intersects parallel planes (i.e., the lateral face intersects parallel planes E and E”); the intersection of a plane with two parallel planes is two parallel lines.
→ We can then conclude that ABYX is a parallelogram.
Therefore, AB = XY.
→ We can make similar arguments to show BC YZ, and AC XZ.
By SSS, ∆ABC ≅ ∆XYZ.
→ How does this argument allow us to prove that any prism, no matter what polygon the base is, has cross- section s congruent to the base?
We can decompose the base into triangles and use those triangles to decompose the prism into triangular prisms.