Eureka Math Geometry Module 2 Mid Module Assessment Answer Key
Eureka Math Geometry Module 2 Mid Module Assessment Answer Key
Question 1.
The coordinates of ∆ABC are shown on the coordinate plane below. ∆ABC is dilated from the origin by scale factor r = 2.
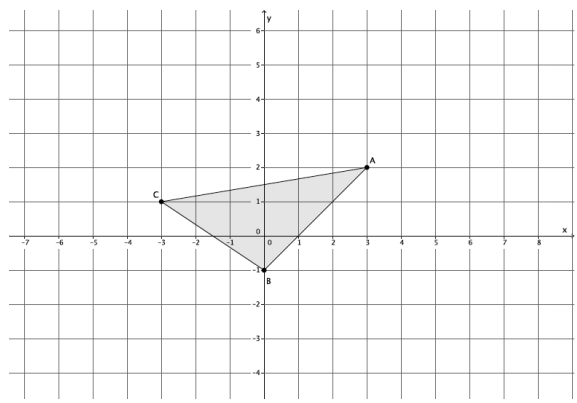
a. Identify the coordinates of the dilated ∆\(A^{\prime} B^{\prime} C^{\prime}\).
Answer:
Point A = (3, 2), then \(A^{\prime}\) = (2×(3), 2×(2)) = (6, 4)
Point B = (0, -1), then \(B^{\prime}\) = (2×(0), 2×(–1)) = (0, -2)
Point 𝐠= (-3, 1), then \(C^{\prime}\) = (2×(–3), 2×(1)) = (-6, 2)
b. Is a ∆\(A^{\prime} B^{\prime} C^{\prime}\) – ∆ABC? Explain.
Answer:
Yes. The side lengths of ∆\(A^{\prime} B^{\prime} C^{\prime}\) are each two times the length of the sides of ∆ABC, and corresponding sides are proportional in length. Also, the corresponding angles are equal in measurement because dilations preserve the measurements of angles.
Question 2.
Points A, B, and C are not collinear, forming ∠BAC. Extend \(\overrightarrow{A B}\) to point P. Line l passes through P and is parallel to segment BC. It meets \(\overrightarrow{A B}\) at point Q.
a. Draw a diagram to represent the situation described.
Answer:
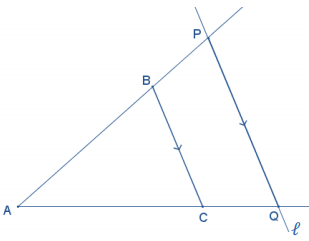
b. Is \(\overline{P Q}\) longer or shorter than \(\overline{B C}\)?
Answer:
\(\overline{P Q}\) is longer than\(\overline{B C}\).
c. Prove that ∆ABC ~ ∆APQ.
Answer:
\(\overline{P Q} \| \overline{B C}\). Since corresponding angles are equal in measure, then m∠ABC = m∠APQ. Additionally, m∠A = m∠A. Then ∆ABC ~ ∆APQ by AA similarity criterion.
d. What other pairs of segments in this figure have the same ratio of lengths that \(\overline{P Q}\) has to \(\overline{B C}\)?
Answer:
PA : BA, QA : CA
Question 3.
There is a triangular floor space ∆ABC in a restaurant. Currently, a square portion DEFG is covered with tile. The owner wants to remove the existing tile and then tile the largest square possible within ABC, keeping one edge of the square on \(\overline{A C}\).
a. Describe a construction that uses a dilation with center A that can be used to determine the maximum square \(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\) within ∆ABC with one edge on \(\overline{A C}\).
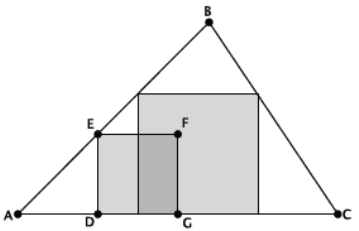
Answer:
- Use A as a center of dilation.
- Draw \(\overrightarrow{A F}\) through BC.
- Label the intersection of \(\overrightarrow{A F}\) and BC as \(F^{\prime}\).
- Construct \(\overline{E^{\prime} F^{\prime}}\) parallel to EF, where \(E^{\prime}\) is the intersection of AB and the parallel line.
- Construct \(\overline{F^{\prime} G^{\prime}}\) parallel to FG, where \(G^{\prime}\) is the intersection of AC and the parallel line.
- Construct \(\overline{E^{\prime} D^{\prime}}\) parallel to ED, where \(D^{\prime}\) is the intersection of AC and the parallel line.
- Connect \(D^{\prime}\), \(E^{\prime}\), \(F^{\prime}\), \(G^{\prime}\).
b. What is the scale factor of \(\overline{F G}\) to \(\overline{F^{\prime} G^{\prime}}\) in terms of the distances \(\overline{A F}\) and \(\overline{A F^{\prime}}\)?
Answer:
\(\frac{A F^{\prime}}{A F}\)
c. The owner uses the construction in part (a) to mark off where the square would be located. He measures AE to be 15 feet and E\(E^{\prime}\) to be 5 feet. If the original square is 144 square feet, how many square feet of tile does he need for \(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\)?
Answer:
The distance A\(E^{\prime}\) = 20 ft, so the scale factor from DEFG to \(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\) is \(\frac{20}{15}=\frac{4}{3}\).
Area (\(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\)) = \(\left(\frac{4}{3}\right)^{2}\) Area (DEFG)
Area (\(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\)) = \(\frac{16}{9}\)(144)
Area (\(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\)) = 256
The owner needs 256 square feet of tile for \(D^{\prime} E^{\prime} F^{\prime} G^{\prime}\).
Question 4.
ABCD is a parallelogram, with the vertices listed counterclockwise around the figure. Points M, N, O, and P are the midpoints of sides \(\overline{A B}\), \(\overline{B C}\), \(\overline{C D}\), and \(\overline{D A}\), respectively. The segments MO and NP cut the parallelogram into four smaller parallelograms, with the point W in the center of ABCD as a common vertex.
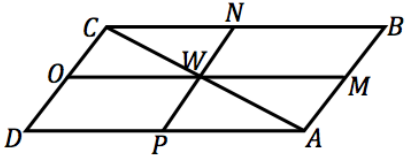
a. Exhibit a sequence of similarity transformations that takes ∆AMW to ∆CDA. Be specific in describing the parameter of each transformation; for example, if describing a reflection, state the line of reflection.
Answer:
Answers will vary (e.g., 180˚ rotation about W; dilation with center of dilation C).
b. Given the correspondence in ∆AMW similar to ∆CDA, list all corresponding pairs of angles and corresponding pairs of sides. What is the ratio of the corresponding pairs of angles? What is the ratio of the corresponding pairs of sides?
Answer:
∠MAW corresponds to ∠DCA; ∠AMW corresponds to ∠CDA; ∠AWM corresponds to ∠CAD. \(\overline{A M}\) corresponds to \(\overline{C D}\); \(\overline{M W}\) corresponds to \(\overline{D A}\); \(\overline{W A}\) corresponds to \(\overline{A C}\).
The ratio of corresponding pairs of angles is 1 : 1.
The ratio of corresponding pairs of sides is 1 : 2.
Question 5.
Given two triangles, ∆ABC and ∆DEF, m∠CAB = m∠FDE, and m∠CBA = m∠FED. Points A, B, D, and E lie on line l as shown. Describe a sequence of rigid motions and/or dilations to show that ∆ABC ~ ∆DEF, and sketch an image of the triangles after each transformation.
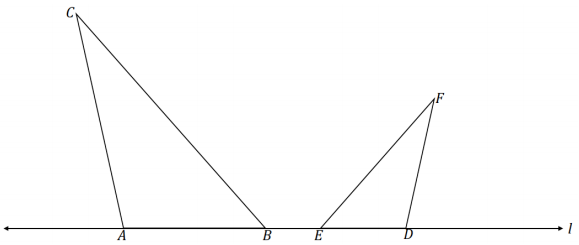
Answer:
Reflect ΔDEF over the perpendicular bisector of \(\overline{B E}\). The reflection takes E to B and D to a
point on line AB. Since angle measures are preserved in rigid motions, F must map to a point on \(\overline{B C}\).
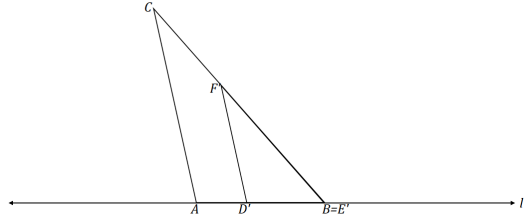
→ By the hypothesis, m∠A = m∠D; therefore, \(\overline{D^{\prime} F^{\prime}} \| \overline{A C}\) since corresponding angles are equal in measure.
→ Since dilations map a segment to a parallel line segment, dilate ∆\(D^{\prime} E^{\prime} F^{\prime}\) about \(E^{\prime}\) and by scale factor r = \(\frac{B A}{B D^{\prime}}\) and that sends \(D^{\prime}\) to A.
→ By the dilation theorem, \(F^{\prime}\) goes to C.
Question 6.
∆JKL is a right triangle; \(\overline{N P}\) ⊥\(\overline{K L}\), \(\overline{N O}\) ⊥ \(\overline{J K}\), \(\overline{M N}\) || \(\overline{O P}\)
a. List all sets of similar triangles. Explain how you know.
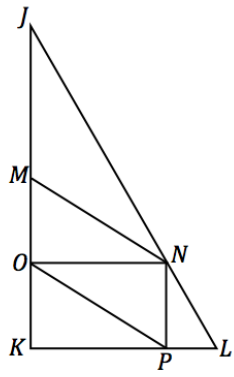
Answer:
Set 1
- ∆MNO
- ∆PON
- ∆OPK
Set 2
- ∆JON
- ∆JKL
- ∆NPL
The triangles are similar because of the AA criterion.
b. Select any two similar triangles, and show why they are similar.
Answer:
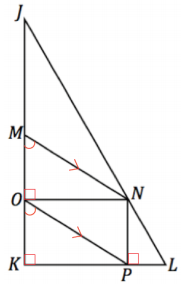
Possible response:
- ∆MNO ~ ∆PON by the AA criterion.
- ∠K is a right angle since ∆JKL is a right triangle.
- ∠MON is a right angle since \(\overline{\mathrm{NO}} \perp \overline{\mathrm{JK}}\)
m∠NMO = m∠POK since \(\overline{M N} \| \overline{O P}\)̅, and \(\overline{J K}\) is a transversal that intersects \(\overline{M N}\) and \(\overline{O P}\); corresponding ∠’s are equal in measure. - Therefore, by the AA criterion, ∆MNO ~ ∆PON.
Question 7.
a. The line PQ contains point O. What happens to \(\overleftrightarrow{P Q}\) with a dilation about O and scale factor of r = 2? Explain your answer.
![]()
Answer:
- Since the points P and Q are collinear with the center O, then by definition of a dilation, both P’ and Q’ will also be collinear with the center O.
- The line PQ maps to itself.
b. The line PQ contains point O. What happens to \(\overleftrightarrow{P Q}\) with a dilation about O and scale factor of r = 2? Explain your answer.
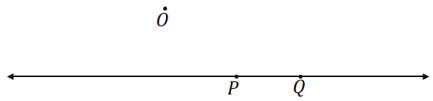
Answer:
The line PQ maps to a parallel line \(P^{\prime} Q^{\prime}\).
Question 8.
Use the diagram below to answer the following questions.
a. State the pair of similar triangles. Which similarity criterion guarantees their similarity?
Answer:
∆DEF ~ ∆FGH
SAS
b. Calculate DE to the hundredths place.
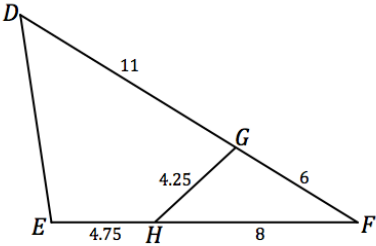
Answer:
\(\frac{D E}{F G}=\frac{D F}{F H}\)
\(\frac{D E}{6}=\frac{17}{8}\)
8 DE = 102
DE ≈ 12.75
Question 9.
In ∆ABC, m∠A is 40°, m∠B is 60°, and m∠C is 80°. The triangle is dilated by a factor of 2 about point P to form ∆\(A^{\prime} B^{\prime} C^{\prime}\). It is also dilated by a factor of 3 about point Q to form ∆\(A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}\) What is the measure of the angle formed by line \(A^{\prime} B^{\prime}\) and line \(B^{\prime \prime} C^{\prime \prime}\) ? Explain how you know.
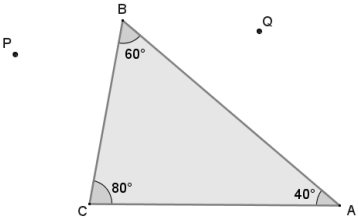
Answer:
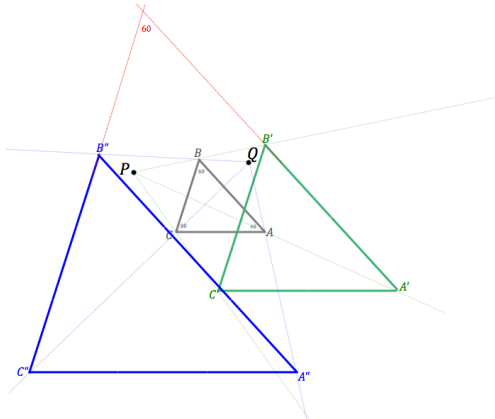
60˚. \(\overline{B^{\prime} C^{\prime}}\) and \(\overline{A^{\prime} B^{\prime}}\) meet to form a 60˚ angle. Since dilations map segments to parallel segments, \(\overline{B^{\prime} C^{\prime}} \| \overline{B^{\prime \prime} C^{\prime \prime}}\). Then the angle formed by lines \(A^{\prime} B^{\prime}\) and \(\mathrm{B}^{\prime \prime} \mathrm{C}^{\prime \prime}\) is a corresponding angle to ∠B and has a measure of 60˚.
Question 10.
In the diagram, |AC| = |CE| = |EG|, and ∠BAC, ∠DCE, and ∠FEG are right. The two lines meet at a point to the right. Are the triangles similar? Why or why not?

Answer:
The triangles are not similar.
If they were similar, then there would have to be a similarity transformation taking A to C, B to D, and C to E. But then the dilation factor for this transformation would have to be 1, since AC = CE.
But since the dilation factor is 1 and \(\overline{C D}\) is the image of \(\overline{A B}\), then it must be true that AB = CD. Additionally, we know that \(\overline{A B}\) is parallel to \(\overline{C D}\), and since ∠BAC and ∠DCE are right, this implies ACDB is a rectangle. This implies that \(\overline{B D}\) is parallel to \(\overline{A C}\), but this is contrary to the given.
Question 11.
The side lengths of the following right triangle are 16, 30, and 34. An altitude of a right triangle from the right angle splits the hypotenuse into line segments of length x and y.
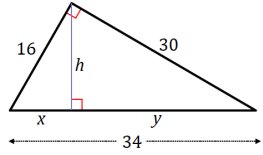
a. What is the relationship between the large triangle and the two sub-triangles? Why?
Answer:
An altitude drawn from the vertex of the right angle of a right triangle to the hypotenuse divides the right triangle into two sub-triangles that are similar to the original triangle by the AA criterion.
b. Solve for h, x, and y.
Answer:
\(\frac{h}{30}=\frac{16}{34}\)
h = \(\frac{240}{17}\)
\(\frac{x}{16}=\frac{16}{34}\)
x = \(\frac{128}{17}\)
\(\frac{y}{30}=\frac{30}{34}\)
y = \(\frac{450}{17}\)
c. Extension: Find an expression that gives h in terms of x and y.
Answer:
The large triangle is similar to both sub-triangles, and both sub-triangles are, therefore, similar. Then,
\(\frac{x}{h}=\frac{h}{y}\)
h2 = xy
h = \(\sqrt{x y}\)
Question 12.
The sentence below, as shown, is being printed on a large banner for a birthday party. The height of the banner is 18 inches. There must be a minimum 1-inch margin on all sides of the banner. Use the dimensions in the image below to answer each question.

a. Describe a reasonable figure in the plane to model the printed image.
Answer:
The sentence can be modeled as a rectangle with dimensions 4.78″ × 0.44″.
b. Find the scale factor that maximizes the size of the characters within the given constraints.
Answer:
The scaled height of the rectangle cannot exceed 16″ to allow for 1″ margins above and below on the banner.
16 = k(0.44), where k represents the scale factor of the banner;
k = \(\frac{16}{0.44}\) = \(\frac{400}{11}\) = 36\(\frac{4}{11}\)
c. Wnat is the total length ot tne banner asea on your answer to part (a)?
Answer:
Using the scale factor from part (a),
y = (\(\frac{400}{11}\)) . (4.78)
y = 173\(\frac{9}{11}\)
The total length of the image in the banner is 173\(\frac{9}{11}\) inches; however, the banner must
have a minimum 1″ margin on all sides of the image, so the banner must be at least 2″ longer. The total length of the banner must be at least 175\(\frac{9}{11}\) inches.