Worksheet on Exact Divisibility helps the students to score better grades in the exams. Any number which leaves the remainder as 0 is known as Exact Divisibility. We have conducted Divisibility Tests for various numbers to make you understand what the exact divisibility is. There are different methods in the division. Go through this page to learn the simple methods of exact divisibility. Check Divisibility Tests for 2, 3, 4, 5, 6, 7, 8, 9, and 10 on the Exact Divisibility Worksheet.
Do Refer:
Worksheet on Exact Divisibility with Solutions
Question 1
Circle the number which is exactly divisible by 2?
A. 24
B. 36
C. 25
D. 43
E. 7
Solution:
A. 24
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
24 has the last digit. So it is exactly divisible by 2.
24 ÷ 2 = 12
24 is exactly divisible by 2.
B. 36
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
36 has the last digit. So it is exactly divisible by 2.
36 ÷ 2 = 18
36 is exactly divisible by 2.
C. 25
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
5 is not divisible by 2.
Thus 25 is not exactly divisible by 25.
D. 43
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
3 is not divisible by 2.
Thus 43 is not exactly divisible by 43.
E. 7
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
7 is not divisible by 2.
Thus A, B are exactly divisible by 2.
Question 2
Which of the following numbers are exactly divisible by 3?
35, 15, 21, 315, 41
Solution:
35 – 3 + 5 = 8
8 is not divisible by 3
35 is not exactly divisible by 3.
15 – 1 + 5 = 6
6 is exactly divisible by 3.
15 is exactly divisible by 3.
21 – 2 + 1 = 3
3 is exactly divisible by 3.
Thus 21 is exactly divisible by 3.
315 = 3 + 1 + 5 = 9
9 is exactly divisible by 3.
That means 315 is exactly divisible by 3.
41 – 4 + 1 = 5
5 is not exactly divisible by 3.
Thus 41 is not exactly divisible by 3.
Question 3
Check whether 1624 is exactly divisible by 4.
Solution:
Any number that is divisible by 2 will be divisible by 4.
The last digit 4 is divisible by 4 so it will be divisible by 4.
1624 ÷ 4 = 406
Thus 1624 is exactly divisible by 4.
Question 4
Find the number which is exactly divisible by 5?
A. 1550
B. 625
C. 1200
D. 1628
Solution:
A. 1550
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
1550 has the last digit as 0. That means 1550 is exactly divisible by 5.
B. 625
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
625 has the last digit as 5. That means 625 is exactly divisible by 5.
C. 1200
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
1200 has the last digit as 0. That means 1200 is exactly divisible by 5.
D. 1628
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
1628 has the last digit as 8.
Thus 1628 is not exactly divisible by 5.
Question 5
Check whether 24 and 36 are exactly divisible by 6.
Solution:
A number that is divisible by 2 and 3 will be divisible by 6.
24 and 36 are the multiples of 2 and 3.
24 ÷ 6 = 4
36 ÷ 6 = 6
Thus 24 and 36 are exactly divisible by 6
Question 6
Check if the numbers 49 and 343 are exactly divisible by 7.
Solution:
7 is a prime number. We have to check as per the multiples of 7.
49 = 7 × 7
49 ÷ 7 = 7
Thus 49 is exactly divisible by 7.
343 ÷ 7 = 49
Thus 343 is exactly divisible by 7.
Hence both 49 and 343 are exactly divisible by 7.
Question 7
Test whether 512 exactly divisible by 8.
Solution:
A number that is divisible by 2 and 4 will be divisible by 8.
512 has 2 in its last digit. Thus it is exactly by 8
5 + 1 + 2 = 8
512 ÷ 8 = 64
Thus 512 is exactly divisible by 8.
Question 8
Check whether 108 is exactly divisible by 9.
Solution:
108 – 1 + 0 + 8 = 9
9 is exactly divisible by 9
108 ÷ 9 = 12
Thus 108 is exactly divisible by 9.
Question 9
Check 5040 exactly divisible by 10.
Solution:
Any number that has the last digit as 0 then that number will be exactly divisible by 10.
5040 has 0 in the last digit
Thus 5040 is exactly divisible by 10.
Question 10
Match the following numbers that are exactly divisible by 2, 3, 5, 7.
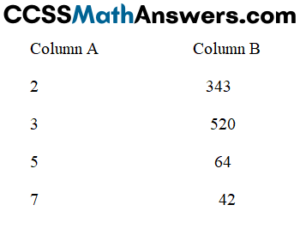
Solution:

Question 11
A number that ends with 5 or 0 is divisible by _________.
Solution:
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
Question 12
A number that ends up with 0 is divisible by __________.
Solution:
Any number that has the last digit as 0 then that number will be exactly divisible by 10.
Question 13
Find the numbers that are exactly divisible by both 2 and 3.
A. 18
B. 312
C. 36
D. 512
Solution:
A. 18
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
18 has the last digit. So it is exactly divisible by 2.
18 ÷ 2 = 9
1 + 8 = 9
9 is exactly divisible by 3.
18 ÷ 3 = 6
Thus 18 is exactly divisible by 2 and 3.
B. 312
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
312 has the last digit. So it is exactly divisible by 2.
312 ÷ 2 = 156
312 is exactly divisible by 2.
312 = 3 + 1 + 2 = 6
6 is exactly divisible by 3.
312 ÷ 3 = 104
Thus 312 is exactly divisible by 2 and 3.
C. 36
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
36 has the last digit. So it is exactly divisible by 2.
36 ÷ 2 = 18
3 + 6 = 9
9 is exactly divisible by 3.
36 ÷ 3 = 12
Thus 36 is exactly divisible by 2 and 3.
D. 512
A number is said to be exactly divisible by 2 only when it has the last digits as 0, 2, 4, 6, 8.
512 has the last digit. So it is exactly divisible by 2.
512 ÷ 2 = 256
512 is exactly divisible by 2.
5 + 1 + 2 = 8
8 is not divisible by 3.
Thus 512 is not exactly divisible by 3.
Question 14
Find the numbers that are exactly divisible by both 5 and 10.
A. 1250
B. 5005
C. 1600
D. 900
Solution:
A number that has the last digit as 0 or 5 then that number will be exactly divisible by 5.
Any number that has the last digit as 0 then that number will be exactly divisible by 10.
To find whether the given numbers are exactly divisible by 5 and 10 we have to check the last digits.
A. 1250
It has 0 in the last digit so the number 1250 is exactly divisible by 5 and 10.
B. 5005
It has 5 in the last digit so the number 5005 is exactly divisible by 5, not 10.
C. 1600
It has 0 in the last digit so the number 1600 is exactly divisible by 5 and 10.
D. 900
It has 0 in the last digit so the number 900 is exactly divisible by 5 and 10.
Question 15
Find the numbers that are exactly divisible by both 4 and 8.
A.1640
B. 32
C. 80
D. 804
Solution:
A. 1640
16 and 40 are multiples of 4 and 8.
16 and 40 are divisible by both 4 and 8
1640 ÷ 4 = 410
1640 ÷ 8 = 205
1640 is exactly divisible by both 4 and 8.
Thus the quotient is 410 and 205 and leaves the remainder as 0.
B. 32
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32…
Multiples of 8 are 8, 16, 24, 32…
32 ÷ 4 = 8
32 ÷ 8 = 4
Thus 32 is exactly divisible by both 4 and 8.
C. 80
80 = 8 + 0 = 8
8 is exactly divisible by 4 and 8
80 ÷ 4 = 20
80 ÷ 8 = 10
Thus 80 is exactly divisible by both 4 and 8.
D. 804
8 + 0 + 4 = 12
12 is divisible by 4 but not 8.
804 ÷ 4 = 201
804 ÷ 8 = 100.5
Thus 804 is exactly divisible by 4 but not 8.
