Engage NY Eureka Math Geometry Module 2 Lesson 34 Answer Key
Eureka Math Geometry Module 2 Lesson 34 Opening Exercise Answer Key
Opening Exercise:
a. Dan was walking through a forest when he came upon a sizable tree. Dan estimated he was about 40 meters away from the tree when he measured the angle of elevation between the horizontal and the top of the tree to be 35 degrees. If Dan is about 2 meters tall, about how tall is the tree?
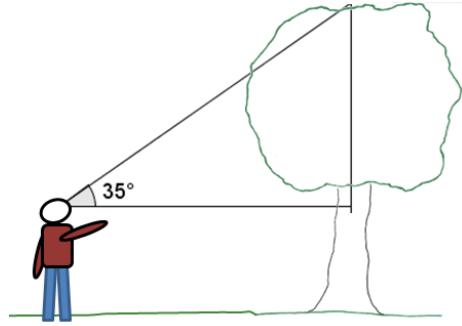
Answer:
Let x represent the vertical distance from Dan’s eye level to the top of the tree.
tan 35 = \(\frac{x}{40}\)
40 tan 35 = x
28 ≈ x
The height of the tree is approximately 30 m.
b.
Dan was pretty impressed with this tree until he turned around and saw a bigger one, also 40 meters away in the other direction. “Wow,” he said. “I bet that tree is at least 50 meters tall!” Then, he thought a moment. “Hmm … if it is 50 meters tall, I wonder what angle of elevation I would measure from my eye level to the top of the tree?” What angle will Dan find if the tree is 50 meters tall? Explain your reasoning.
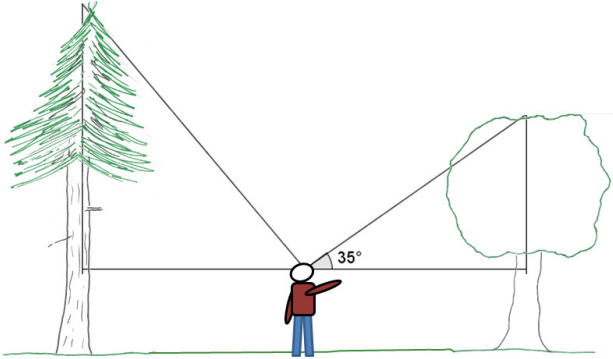
Answer:
Let x represent the angle measure from the horizontal to the top of the tree.
tan x = \(\frac{50}{40}\)
tan x = \(\frac{5}{4}\)
tan x = 1.25
Eureka Math Geometry Module 2 Lesson 34 Exercise Answer Key
Exercises 1 – 5:
Exercise 1.
Find the measure of angles a through d to the nearest degree.
a. 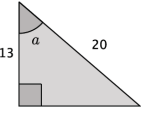
Answer:
arccos(\(\frac{13}{20}\)) ≈ 49 m∠a
b. 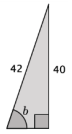
Answer:
arcsin (\(\frac{40}{42}\)) ≈ 72 m∠b
c. 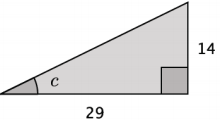
Answer:
arctan (\(\frac{14}{29}\)) ≈ 26° m∠c
d. 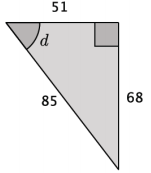
Answer:
Several solutions are acceptable. One is shown below.
arccos (\(\frac{51}{85}\)) ≈ 53, m∠d = 53°
Exercise 2.
Shelves are being built in a classroom to hold textbooks and other supplies. The shelves will extend 10 in. from the wall. Support braces will need to be installed to secure the shelves. The braces will be attached to the end of the shelf and secured 6 in. below the shelf on the wall. What angle measure will the brace and the shelf make?
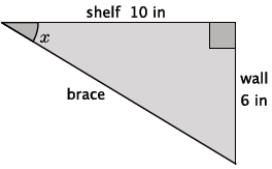
Answer:
arctan(\(\frac{6}{10}\)) ≈ 31
The angle measure between the brace and the shelf is 31°.
Exercise 3.
A 16 ft. ladder leans against a wall. The foot of the ladder is 7 ft. from the wall.
a. Find the vertical distance from the ground to the point where the top of the ladder touches the wall.
Answer:
Let x represent the distance from the ground to the point where the top of the ladder touches the wall.
162 = 72 + x2
162 – 72 = x2
207 = x2
14 ≈ x
The top of the ladder is 14 ft. above the ground.
b. Determine the measure of the angle formed by the ladder and the ground.
Answer:
arccos (\(\frac{7}{16}\)) ≈ 64
The angle formed by the ladder and the ground is approximately 64°.
Exercise 4.
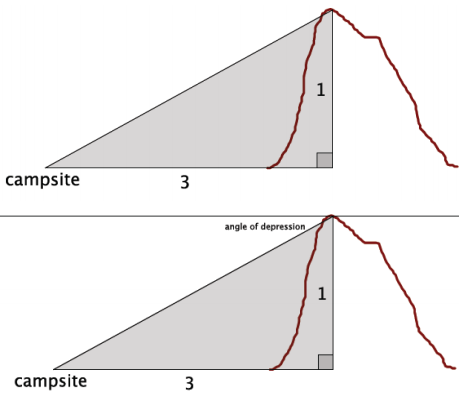
A group of friends have hiked to the top of the Mile High Mountain. When they look down, they can see their campsite, which they know is approximately 3 miles from the base of the mountain.
a. Sketch a drawing of the situation.
Answer:

b. What is the angle of depression?
Answer:
arctan (\(\frac{3}{1}\)) ≈ 72
The angle of depression is approximately 18°.
Exercise 5.
A roller coaster travels 80 ft. of track from the loading zone before reaching its peak. The horizontal distance between the loading zone and the base of the peak is 50 ft.
a. Model the situation using a right triangle.
Answer:
b. At what angle is the roller coaster rising according to the model?
Answer:
arccos (\(\frac{50}{80}\)) ≈ 51
The roller coaster is rising at approximately 51°.
Eureka Math Geometry Module 2 Lesson 34 Problem Set Answer Key
Question 1.
For each triangle shown, use the given information to find the indicated angle to the nearest degree.
a. 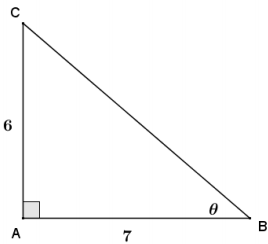
Answer:
tan θ = (\(\frac{6}{7}\))
arctan (\(\frac{6}{7}\)) = θ
θ ≈ 41°
b. 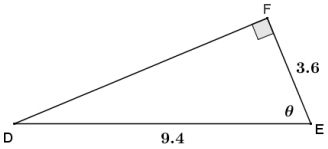
Answer:
cos θ = \(\frac{3.6}{9.4}\)
arccos((\(\frac{6}{7}\)) = θ
θ ≈ 67°
c. 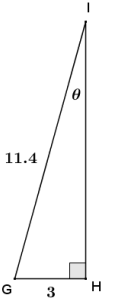
Answer:
sin θ = \(\frac{3}{11.4}\)
arcsin (\(\frac{3}{11.4}\)) = θ
θ ≈ 15°
Question 2.
Solving a right triangle means using given information to find all the angles and side lengths of the triangle. Use arcsin and arccos, along with the given information, to solve right triangle ABC if leg AC = 12 and hypotenuse AB = 15.
Answer:
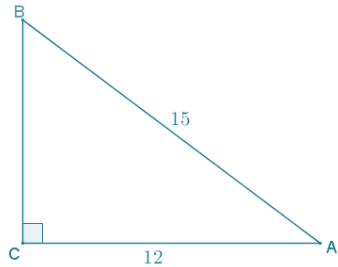
By the Pythagorean theorem, BC = 9.
sin B = \(\frac{12}{15}\)
arcsin(\(\frac{12}{15}\)) = m∠B
m∠B ≈ 53°
cos A = \(\frac{12}{15}\)
arccos(\(\frac{12}{15}\)) = m∠A
m∠A ≈ 37°
b. Once you have found the measure of one of the acute angles in the right triangle, can you find the measure of the other acute angle using a different method than those used in this lesson? Explain.
Answer:
Yes. We could use the angle sum of a triangle after finding the measure of one acute angle.
Question 3.
A pendulum consists of a spherical weight suspended at the end of a string whose other end is anchored at a pivot point P. The distance from P to the center of the pendulum’s sphere, B, is 6 inches. The weight is held so that the string is taut and horizontal, as shown to the right, and then dropped.
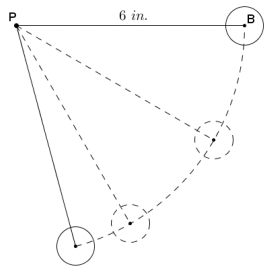
a. What type of path does the pendulum’s weight take as it swings?
Answer:
Since the string is a constant length, the path of the weight is circular.
b. Danni thinks that for every vertical drop of 1 inch that the pendulum’s weight makes, the degree of rotation is 15°. Do you agree or disagree with Danni? As part of your explanation, calculate the degree of rotation for every vertical drop of 1 inch from 1 inch to 6 inches.
Answer:
Disagree A right triangle can model the pendulum and its vertical drops as shown in the diagrams.
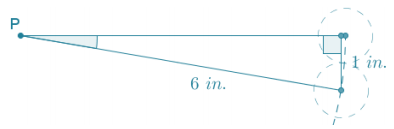
The angle of rotation about P for a vertical drop of 1 inch is equal to the arcsin (\(\frac{1}{6}\)), which is approximately 10°.
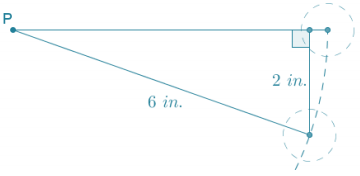
The angle of rotation about P for a vertical drop of 2 inches is equal to the arcsin (\(\frac{2}{6}\)), which is approximately 20°.
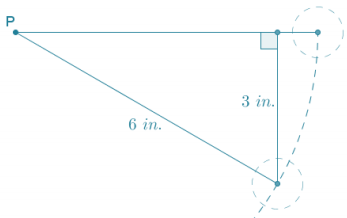
The angle of rotation about P for a vertical drop of 3 inches is equal to the arcs in (\(\frac{3}{6}\)), which is 30°.
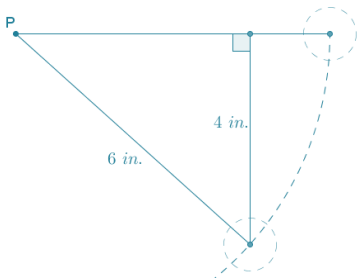
The angle of rotation about P for a vertical drop of 4 inches is equal to the arcsin (\(\frac{4}{6}\)), which is approximately 42°.
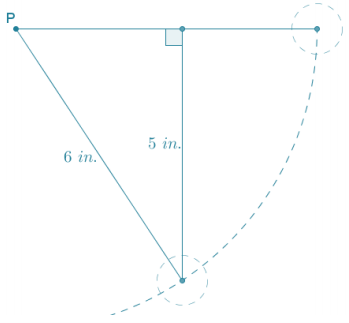
The angle of rotation about P for a vertical drop of 5 inches is equal to the arcsin (\(\frac{5}{6}\)), which is approximately 56°.
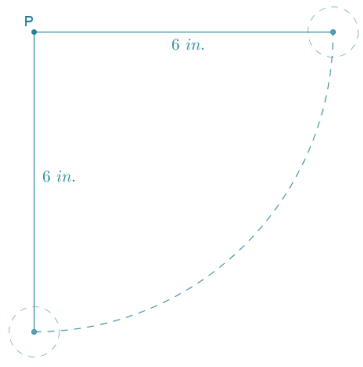
The pendulum’s weight will be at its maximum distance below the pivot point, which means that the weight must be directly below the pivot point. This means that the string would be perpendicular to the horizontal starting position; therefore, the degree of rotation would be 90°.
Question 4.
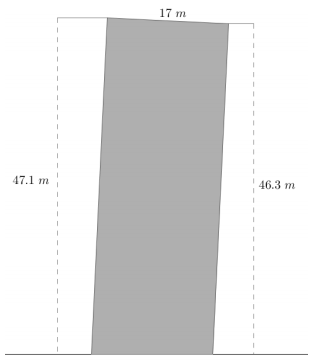
A stone tower was built on unstable ground, and the soil beneath It settled under its weight, causing the tower to lean. The cylindrical tower has a diameter of 17 meters. The height of the tower on the low side measured 46. 3 meters and on the high side measured 47. 1 meters. To the nearest tenth of a degree, find the angle that the tower has leaned from its original vertical position.
Answer:
The difference in, heights from one side of the tower to the other is 47.1 m – 46.3 m = 0.8m.
Model the difference in heights and the diameter of the tower using a right trlangla (The right triangle shown below is not drawn to scale).
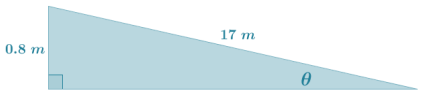
The unknown value θ represents the degree measure that the tower has leaned.
sin θ = \(\frac{0.8}{17}\)
θ = arcsin(\(\frac{0.8}{17}\))
θ ≈ 3
The tower has leaned approximately 3° from its vertical position.
Question 5.
Doug is installing a surveillance camera inside a convenience store. He mounts the camera 8 ft. above the ground and 15 ft. horizontally from the store’s entrance. The camera is meant to monitor every customer who enters and exits the store. At what angle of depression should Doug set the camera to capture the faces of all customers?
Note: This is a modeling problem and therefore will have various reasonable answers.
Answer:
The solution below represents only one of many possible reasonable solutions.
Most adults are between 4\(\frac{1}{2}\) ft. and 6\(\frac{1}{2}\) ft. tall, so the camera should be aimed to capture images within the range of 1\(\frac{1}{2}\) ft. to 3\(\frac{1}{2}\) ft. below its mounted height. Cameras capture a range of images, so Doug should mount the camera so that it points at a location in the doorway 2\(\frac{1}{2}\) ft. below its mounted height.
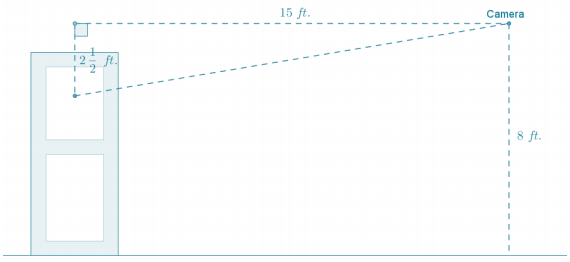
The angle of depression is equal to the arctan \(\left(\frac{2 \frac{1}{2}}{15}\right)\) which is approximately 10°.
Eureka Math Geometry Module 2 Lesson 34 Exit Ticket Answer Key
Question 1.
Explain the meaning of the statement “arcsin(\(\frac{1}{2}\)) = 30°.” Draw a diagram to support your explanation.
Answer:
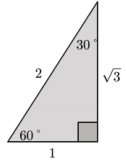
This means that the measure of the angle that has a sine ratio equal to \(\frac{1}{2}\) is 30°.
Question 2.
Gwen has built and raised a wall of her new house. To keep the wall standing upright while she builds the next wall, she supports the wall with a brace, as shown in the diagram below. What is the value of p, the measure of the angle formed by the brace and the wall?
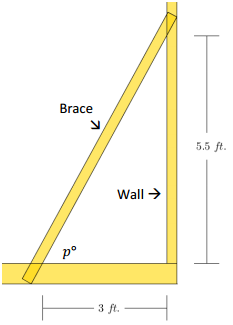
Answer:
arctan \(\frac{5.5}{3}\) = p
61 ≈ p
The measure of the angle formed by the brace and the wall is approximately 61°.