Engage NY Eureka Math Geometry Module 2 Lesson 3 Answer Key
Eureka Math Geometry Module 2 Lesson 3 Example Answer Key
Example 1.
a. Use a ruler and setsquare to draw a line through C parallel to \(\overline{A B}\). What ensures that the line drawn is parallel to \(\overline{A B}\)?
Answer:
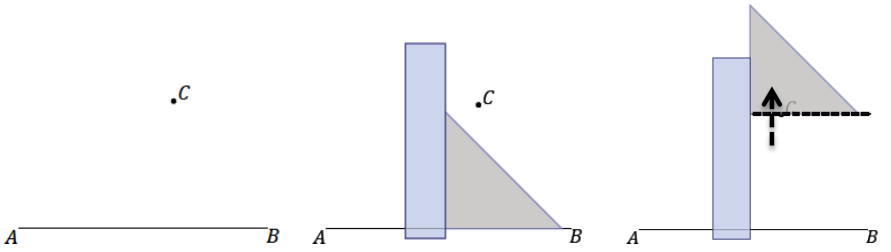
Since the setsquare is in the shape of a right triangle, we are certain that the legs of the setsquare are perpendicular. Then, when one leg is aligned with \(\overline{A B}\), and the other leg is flush against the ruler and can slide along the ruler, the 90° angle between the horizontal leg and the ruler remains fixed; in effect, there are corresponding angles that are equal in measure. The two lines must be parallel.
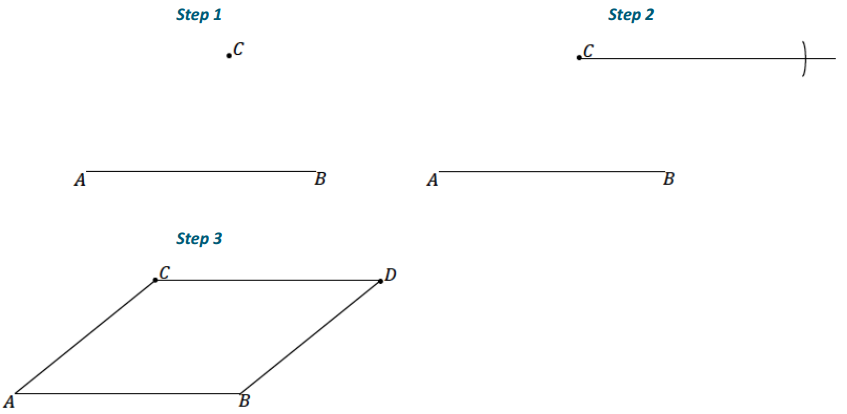
b. Use a ruler and setsquare to draw a parallelogram ABCD around \(\overline{A B}\) and point C.
Answer:
Example 2.
Use the figure below with center O and a scale factor of r = 2 and the following steps to create a scale drawing using the parallel method.
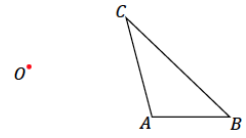
Step 1. Draw a ray beginning at O through each vertex of the figure.
Step 2. Select one vertex of the scale drawing to locate; we have selected A’. Locate A’ on so that \(\overrightarrow{O A}\) = 2OA.
Step 3. Align the setsquare and ruler as in the image below; one leg of the setsquare should line up with side \(\overline{A B}\), and the perpendicular leg should be flush against the ruler.
Step 4. Slide the setsquare along the ruler until the edge of the setsquare passes through A’. Then, along the perpendicular leg of the setsquare, draw the segment through A’ that is parallel to \(\overline{A B}\) until it intersects with \(\overrightarrow{O B}\) and label this point B’.
Step 5. Continue to create parallel segments to determine each successive vertex point. In this particular case, the setsquare has been aligned with \(\overline{A C}\). This is done because, In trying to create a parallel segment from \(\overline{B B}\) the parallel segment was not reaching B’. This could be remedied with a larger setsquare and longer ruler, but it is easily avoided by working on the segment parallel to \(\overline{A C}\) instead.
Step 6. Use your ruler to join the final two unconnected vertices.
Answer:
Step 1. Draw a ray beginning at O through each vertex of the figure.
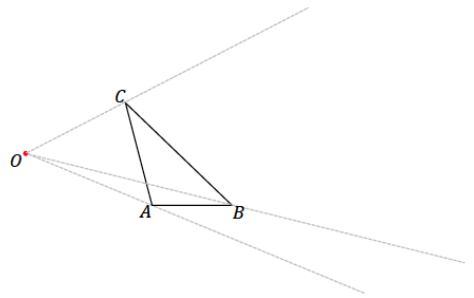
Step 2. Select one vertex of the scale drawing to locate; we have selected A’. Locate A’ on so that \(\overrightarrow{O A}\) = 2OA.
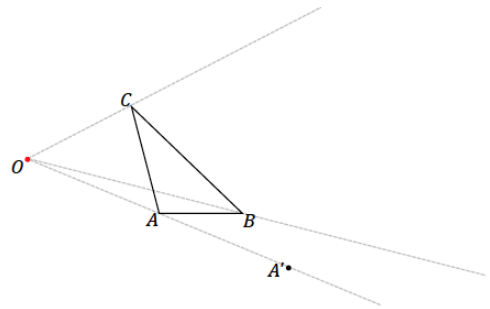
Step 3. Align the setsquare and ruler as in the image below; one leg of the setsquare should line up with side \(\overline{A B}\), and the perpendicular leg should be flush against the ruler.
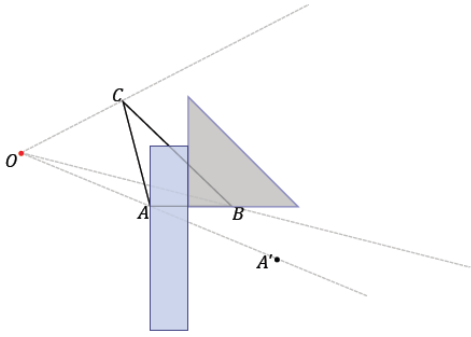
Step 4. Slide the setsquare along the ruler until the edge of the setsquare passes through A’. Then, along the perpendicular leg of the setsquare, draw the segment through A’ that is parallel to \(\overline{A B}\) until it intersects with \(\overrightarrow{O B}\) and label this point B’.
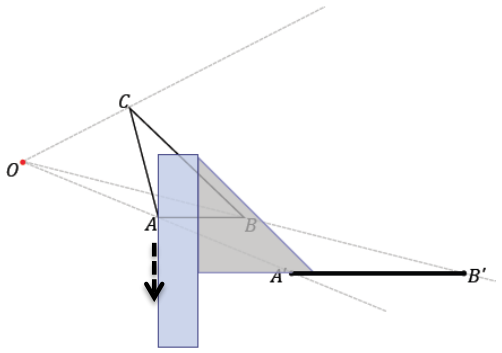
Step 5. Continue to create parallel segments to determine each successive vertex point. In this particular case, the setsquare has been aligned with \(\overline{A C}\). This is done because, In trying to create a parallel segment from \(\overline{B B}\) the parallel segment was not reaching B’. This could be remedied with a larger setsquare and longer ruler, but it is easily avoided by working on the segment parallel to \(\overline{A C}\) instead.
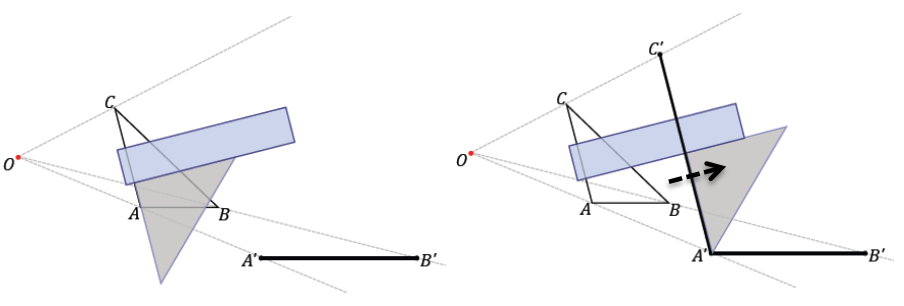
Step 6. Use your ruler to join the final two unconnected vertices.
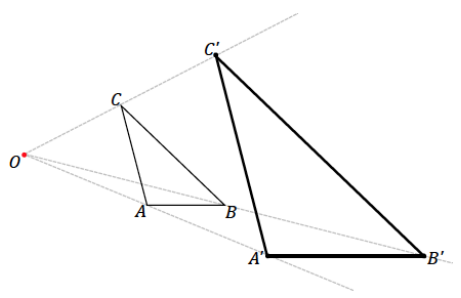
Eureka Math Geometry Module 2 Lesson 3 Opening Exercise Answer Key
Dani dilated ∆ ABC from center O, resulting In ∆ A’B’C’. She says that she completed the drawing using parallel lines. How could she have done this? Explain.
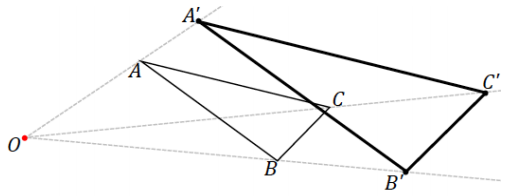
Answer:
Accept reasonable suggestions from students and proceed to Example 1.
Eureka Math Geometry Module 2 Lesson 3 Exercise Answer Key
Exercise 1.
With a ruler and setsquare, use the parallel method to create a scale drawing of WXYZ by the parallel method. W’ has already been located for you. Determine the scale factor of the scale drawing. Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that corresponding angles are equal in measurement.
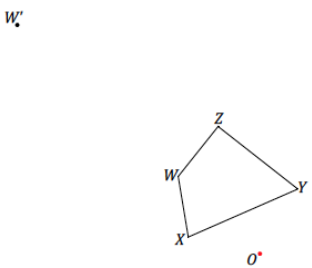
Answer:
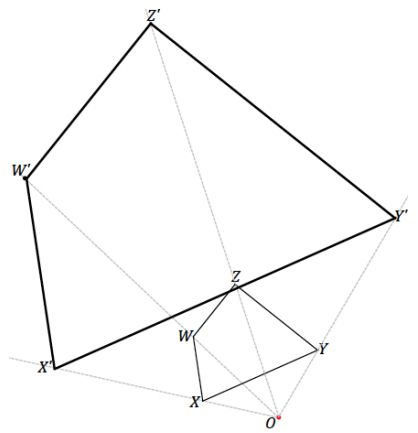
The scale factor is 3. Verification of the enlarged figure should show that the length of each segment in the scale
drawing is three times the length of each segment in the original figure (e.g., W’X’ = 3 (WX)). The angle measurements are m∠W = 132°, m∠X = 76°, m∠Y = 61°, and m∠Z = 91°.
Exercise 2.
With a ruler and setsquare, use the parallel method to create a scale drawing of DEFG about center O with scale factor r = \(\frac{1}{2}\). Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that the corresponding angles are equal in measurement.
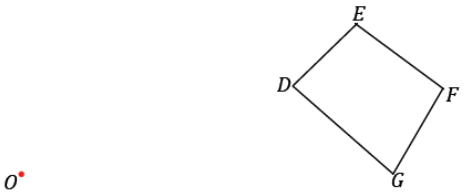
Answer:
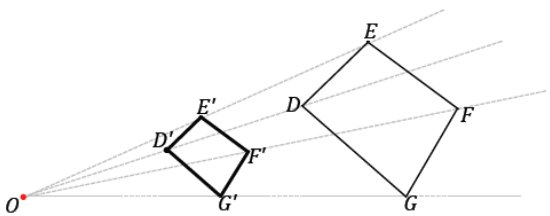
Verification of the reduced figure should show that the length of each segment in the scale drawing is one half the length of each segment in the original figure, (e.g., D’E’ = \(\frac{1}{2}\) (DE)). The angle measurements are m∠D = 85°, m∠E = 99°, m∠F = 97°, and m∠G = 79°.
Exercise 3.
With a ruler and setsquare, use the parallel method to create a scale drawing of pentagon PQRST about center O with scale factor r = \(\frac{5}{2}\) Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that corresponding angles are equal in measurement.
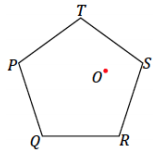
Answer:
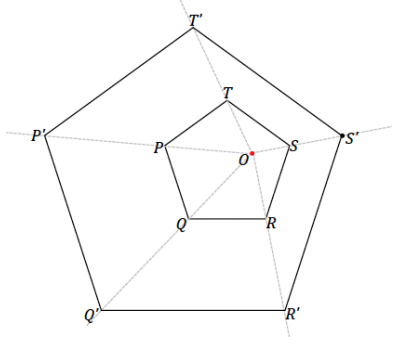
Verification of the enlarged figure should show that the length of each segment in the scale drawing is two-and-a half times the length of each segment in the original figure (e.g., P’T’ = \(\frac{5}{2}\) (PT)). Each of the angles has a measurement of 108°.
Eureka Math Geometry Module 2 Lesson 3 Problem Set Answer Key
Question 1.
With a ruler and setsquare, use the parallel method to create a scale drawing of the figure about center O. One vertex of the scale drawing has been provided for you.
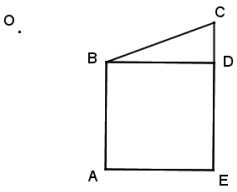
Answer:
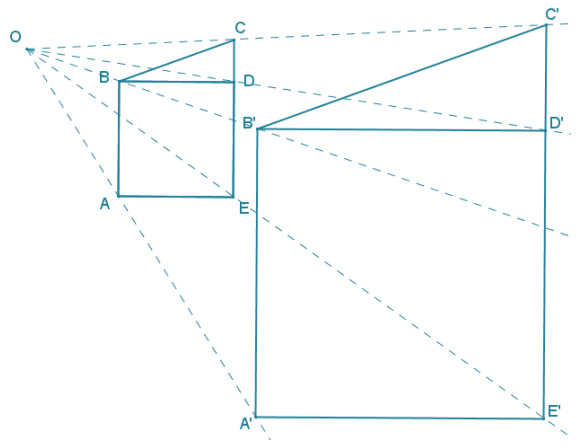
Determine the scale factor. Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that the corresponding angles are equal in measurement.
Answer:
The scale factor is r = \(\frac{5}{2}\). The measurements of the angles in the figure are mLA mLB mz.D mLE = 90°, m∠DBC = 20°, m∠CDB = 90°, and m∠C = 70°. All side-length measurements of the scale drawing are in the constant ratio of 5:2.
Question 2.
With a ruler and setsquare, use the parallel method to create a scale drawing of the figure about center O and scale factor r = \(\frac{1}{3}\). Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and the corresponding angles are equal in measurement.
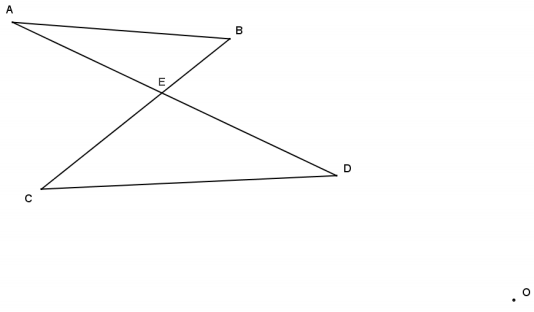
Answer:
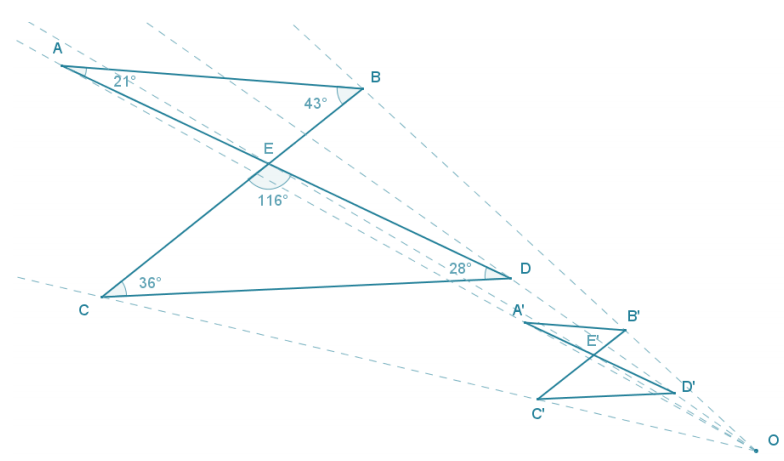
The measurements of the angles in the figure are m∠A = 21°, m∠B = 43°, m∠C = 36°, m∠D = 28°, and m∠CED = m∠BEA = 116°. All side-length measurements of the scale drawing are in the constant ratio of 1:3.
Question 3.
With a ruler and setsquare, use the parallel method to create the following scale drawings about center 0: (1) first use a scale factor of 2 to create ∆ A’B’C’, and (2) then, with respect to ∆ A’B’C’, use a scale factor of \(\frac{2}{3}\) to create scale drawing ∆ A”B”C”. Calculate the scale factor for ∆ A”B”c” as a scale drawing of ∆ ABC. Use angle and side length measurements and the appropriate proportions to verify your answer.
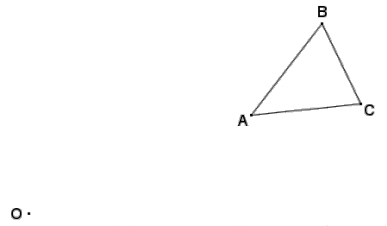
Answer:
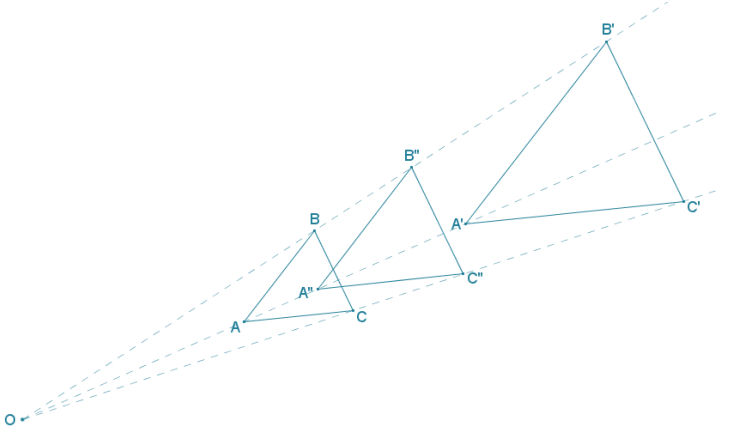
The scale factor of ∆ A‘B’ C’ relative to ∆ AB C is 2. The measurements of the angles in the figure are m∠A ≈ 46°, m∠B ≈ 64°, and m∠70°. The scale factor from ∆ ABC to ∆ A”B”C” is \(\frac{2}{3}\) 2 = \(\frac{4}{3}\). Solutions should show the side-length proportions between ∆ A”B”C” and ∆ ABC: \(\frac{A^{\prime \prime} B^{\prime \prime}}{A B}=\frac{B^{\prime \prime} C^{\prime \prime}}{B C}=\frac{C^{\prime \prime} A^{\prime \prime}}{C A}=\frac{4}{3}\)
Question 4.
Follow the direction in each part below to create three scale drawings of ∆ ABC using the parallel method.
a. With the center at vertex A, make a scale drawing of ∆ ABC with a scale factor of \(\frac{3}{2}\).
b. With the center at vertex B, make a scale drawing of ∆ ABC with a scale factor of \(\frac{3}{2}\).
c. With the center at vertex C, make a scale drawing of ∆ ABC with a scale factor of \(\frac{3}{2}\).
Answer:
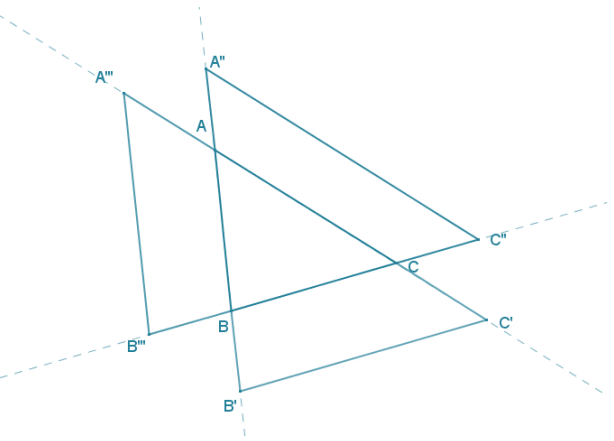
d. What conclusions can be drawn about all three scale drawings from parts (a) – (c)?
Answer:
The three scale drawings are congruent.
AB’ = A”B = \(\frac{3}{2}\)AB Dilation using scale factor \(\frac{3}{2}\).
∠A” ≅ ∠BAC Corresponding ∠‘s formed by parallel lines are congruent.
∠B’ ≅ ∠ABC Corresponding ∠‘s formed by parallel lines are congruent.
∆ AB’C’ ≅ ∆ A”BC” ASA
A similar argument can be used to show ∆ AB’C’ ≅ ∆ A’”B”C, and by transitivity of congruence, all three scale drawings are congruent to each other.
Question 5.
Use the parallel method to make a scale drawing of the line segments in the following figure using the given W’, the image of vertex W, from center O. Determine the scale factor.
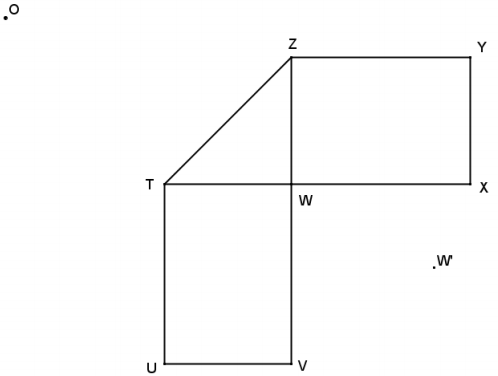
Answer:
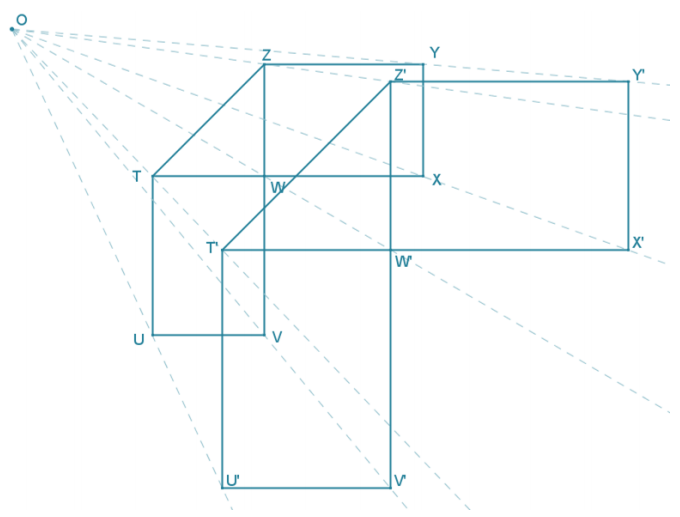
The ratio of OW’: OW is 3:2, so the scale factor is \(\frac{3}{2}\). All corresponding lengths are in the ratio of 3:2.
Use your diagram from Problem 1 to answer this question.
Question 6.
If we switch perspective and consider the original drawing ABCDE to be a scale drawing of the constructed Image A’B’C’D’E’, what would the scale factor be?
Answer:
If the original figure were the scale drawing, and the scale drawing were the original figure, the scale factor would be \(\frac{2}{5}\).
Eureka Math Geometry Module 2 Lesson 3 Exit Ticket Answer Key
With a ruler and setsquare, use the parallel method to create a scale drawing of quadrilateral ABCD about center O with scale factor r = \(\frac{3}{4}\) Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that the corresponding angles are equal in measurement.
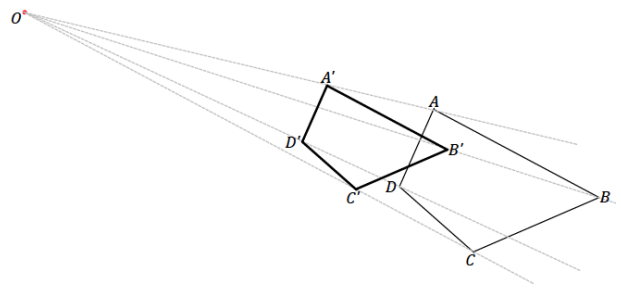
Answer:
The measurements of the angles in the figure are m∠A = 86°, m∠B = 51°, m∠C = 115°, and m∠D 108°. All side- length measurements of the scale drawing should be in the constant ratio of 3:4.
What kind of error in the parallel method might prevent us from having parallel, corresponding sides?
Answer:
If the setsquare is not aligned with the segment of the figure, you will not create a parallel segment. Also, if the setsquare is not perfectly flush with the ruler, it will not be possible to create a segment parallel to the segment of the figure.