Engage NY Eureka Math Geometry Module 2 Lesson 1 Answer Key
Eureka Math Geometry Module 2 Lesson 1 Example Answer Key
Example 1.
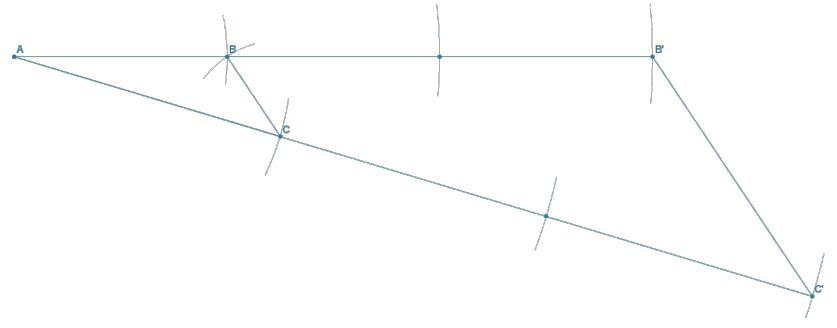
Use construction tools to create a scale drawing of ∆ ABC with a scale factor of r = 2.
Answer:
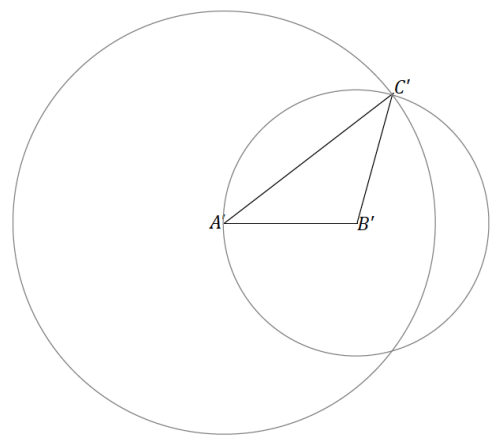
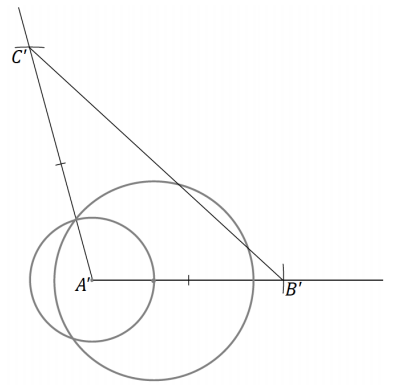
Solution 1: Draw \(\overline{A B}\). To determine B’, adjust the compass to the length of AB. Then reposition the compass so that the point is at B, and mark off the length of \(\overline{A B}\); label the intersection with as B’. C’ is determined in a similar manner. Join B’ to C’.
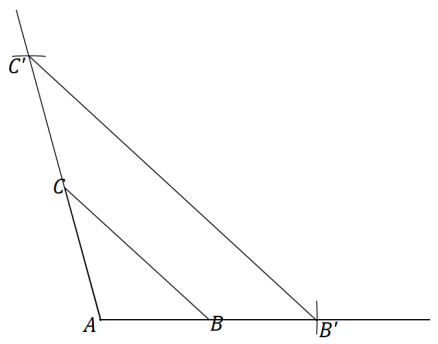
Solution 2: Draw a segment that will be longer than double the length of \(\overline{A B}\). Label one end as A’. Adjust the compass to the length of \(\overline{A B}\), and mark off two consecutive such lengths along the segment, and label the endpoint as B’. Copy ∠A. Determine C’ along the \(\overline{A B}\) in the same way as B’. Join B’ to C’.
Example 2.
Use construction tools to create a scale drawing of ∆ XYZ with a scale factor of r = \(\frac{1}{2}\)
Answer:
Which construction technique have we learned that can be used in this question that was not used in the previous two problems?
We can use the construction to determine the perpendicular bisector to locate the midpoint of two sides of ∆ XYZ.
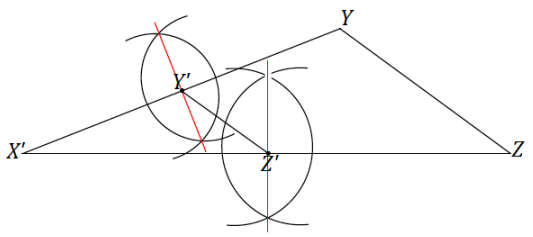
As the solutions to Exercise 1 showed, the constructions can be done on other sides of the triangle (i.e., the perpendicular bisectors of \(\overline{Y Z}\) and \(\overline{X Z}\) are acceptable places to start.)
Eureka Math Geometry Module 2 Lesson 1 Opening Exercise Answer Key

Above is a picture of a bicycle. Which of the images below appears to be a well-scaled image of the original? Why?
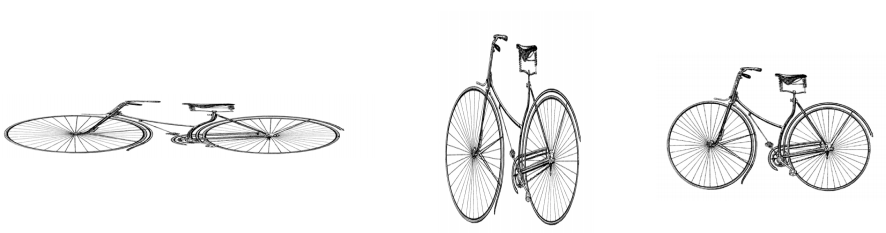
Answer:
Only the third image appears to be a well-scaled image since the image is in proportion to the original.
Eureka Math Geometry Module 2 Lesson 1 Exercise Answer Key
Exercise 1.
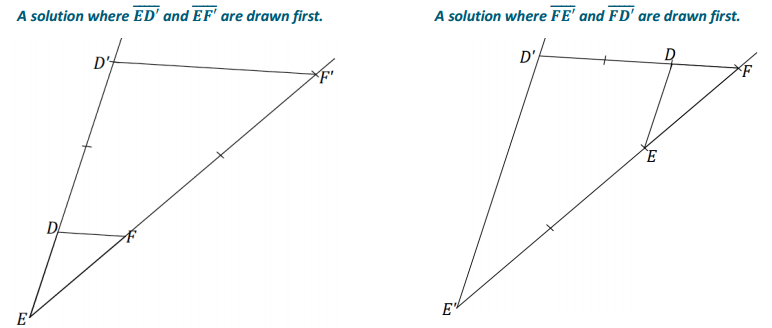
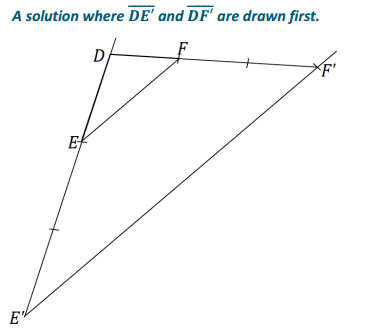
Use construction tools to create a scale drawing of ∆ DEF with a scale factor of r = 3. What properties does your scale drawing share with the original figure? Explain how you know.
Answer:
By measurement, I can see that each side is three times the length of the corresponding side of the original figure and that all three angles are equal in measurement to the three corresponding angles in the original figure.
Exercise 2.
Use construction tools to create a scale drawing of A PQR with a scale factor of r = \(\frac{1}{4}\). What properties do the scale drawing and the original figure share? Explain how you know.
Answer:
By measurement, I can see that all three sides are each one-quarter the lengths of the corresponding sides of the original figure, and all three angles are equal in measurement to the three corresponding angles in the original figure.
Exercise 3.
Triangle EFG is provided below, and one angle of scale drawing ∆ E’F’G’ is also provided. Use construction tools to complete the scale drawing so that the scale factor is r = 3. What properties do the scale drawing and the original figure share? Explain how you know.

Answer:
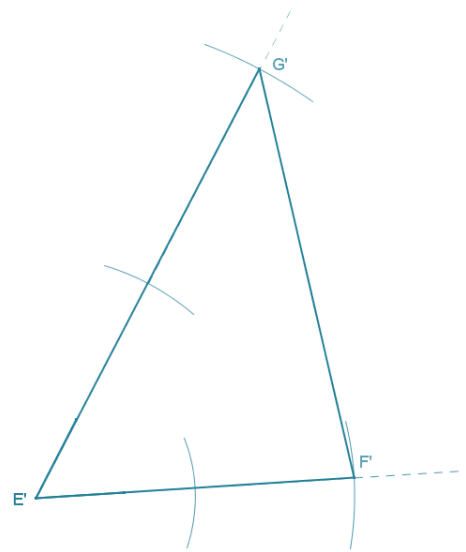
Extend either ray from G’. Use the compass to mark off a length equal to 3EG on one ray and a length equal to 3FG on the other. Label the ends of the two lengths E’ and F’, respectively. Join E’ to F’.

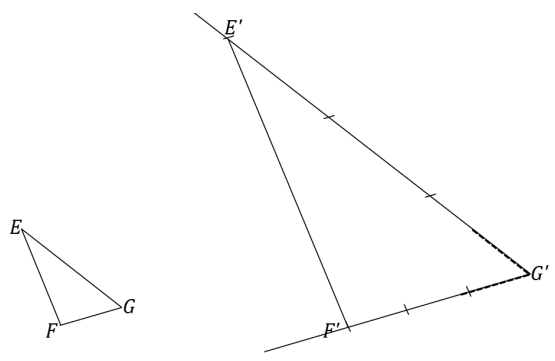
By measurement, I can see that each side is three times the length of the corresponding side of the original figure and that all three angles are equal in measurement to the three corresponding angles in the original figure.
Exercise 4.
Triangle ABC is provided below, and one side of scale drawing ∆ A’B’C’ is also provided. Use construction tools to complete the scale drawing and determine the scale factor.
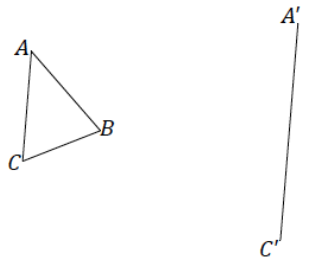
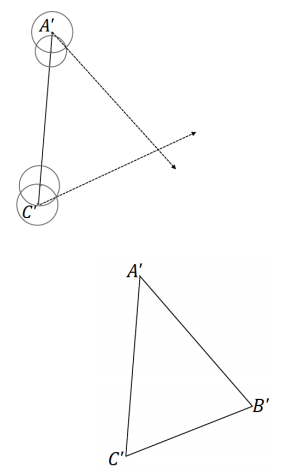
Answer:
One possible solution: We can copy ∠A and ∠C at points A’ and C’ so that the new rays Intersect as shown and call the intersection point B’. By measuring, we can see that AT’ = 2AC, A’B’ = 2AB, and B’C’ = 2BC. We already know that m∠A’ = m∠A and m∠C’ = m∠C. By the triangle sum theorem, m∠B’ = m∠B.
Eureka Math Geometry Module 2 Lesson 1 Problem Set Answer Key
Question 1.
Use construction tools to create a scale drawing of ∆ ABC with a scale factor of r = 3.
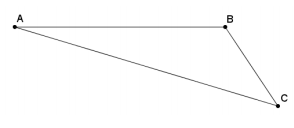
Answer:
Question 2.
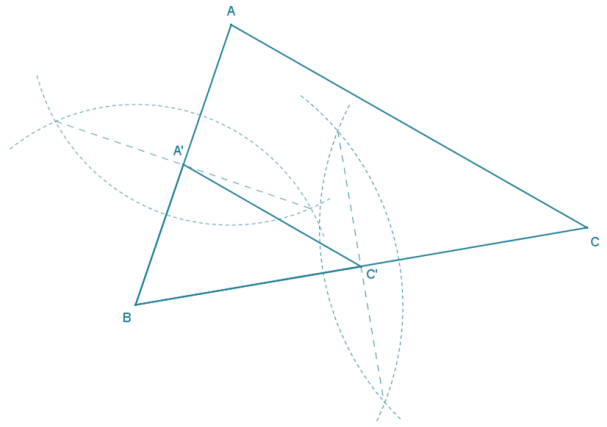
Use construction tools to create a scale drawing of ∆ ABC with a scale factor of r = \(\frac{1}{2}\).
Answer:
Question 3.
Triangle EFG is provided below, and one angle of scale drawing ∆ E’F’G’ Is also provided. Use construction tools to complete a scale drawing so that the scale factor is r = 2.
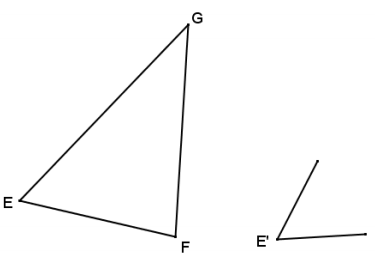
Answer:
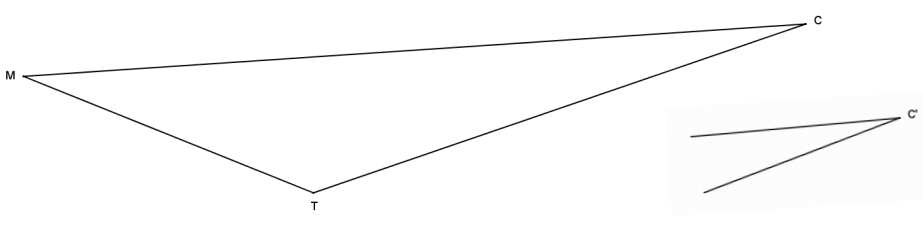
Question 4.
Triangle MTC is provided below, and one angle of scale drawing ∆ M’T’C’ is also provided. Use construction tools to complete a scale drawing so that the scale factor is r =\(\frac{1}{4}\).
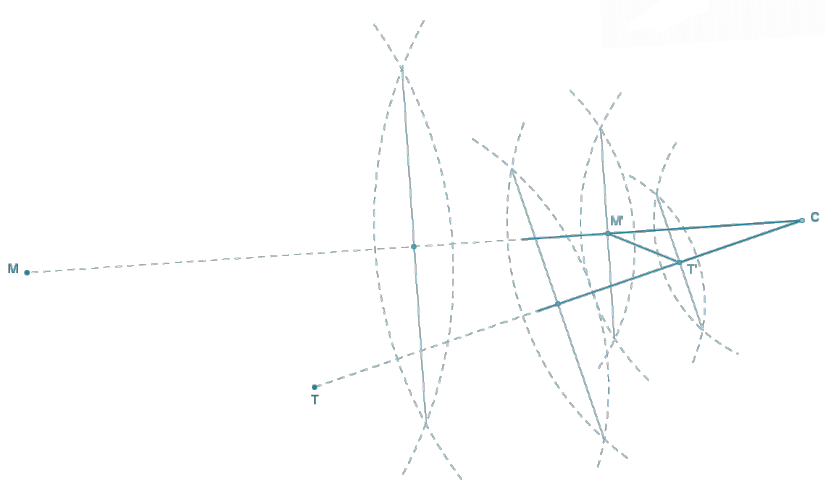
Answer:
Question 5.
Triangle ABC is provided below, and one side of scale drawing ∆ A’B’C’ is also provided. Use construction tools to complete the scale drawing and determine the scale factor.
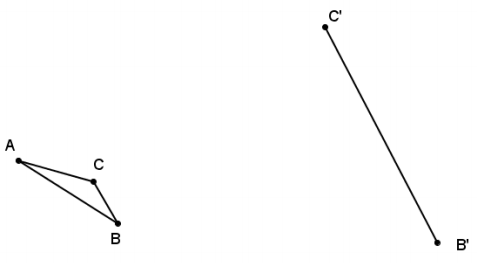
Answer:
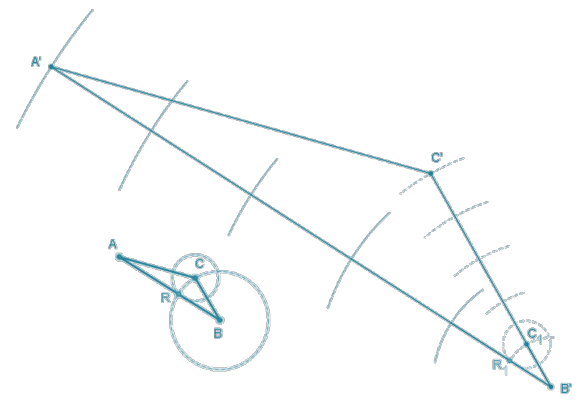
The ratio of B’C’ : BC is 5 : 1, so the scale factor is 5.
Question 6.
Triangle XYZ is provided below, and one side of scale drawing ∆ X’Y’Z’ is also provided. Use construction tools to complete the scale drawing and determine the scale factor.
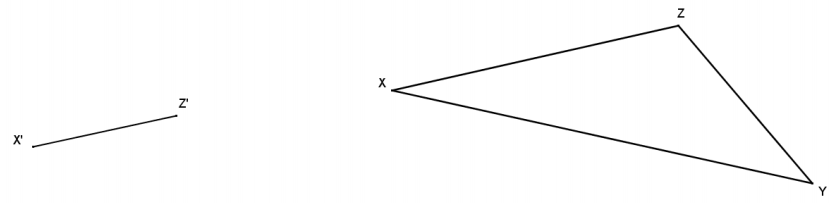
Answer:
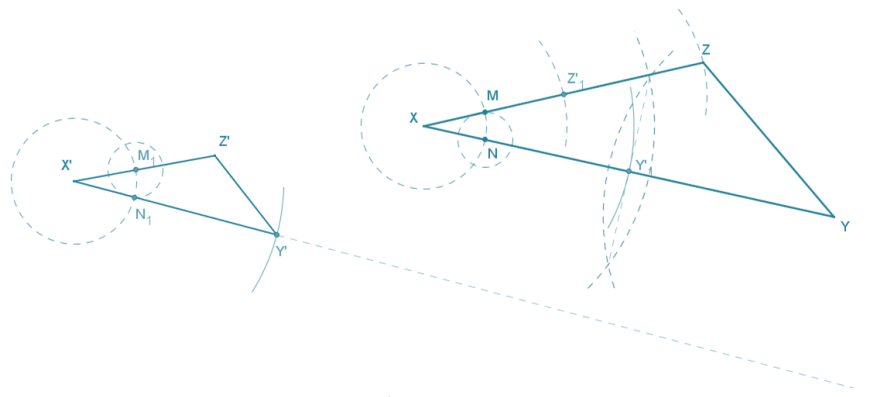
The ratio of X’Z’ : XZ is 1: 2, so the scale factor is \(\frac{1}{2}\).
Question 7.
Quadrilateral GHIJ Is a scale drawing of quadrilateral ABCD with scale factor r. Describe each of the following statements as always true, sometimes true, or never true, and justify your answer.
a. AB = GH
Answer:
Sometimes true, but only if r = 1.
b. m∠ABC = m∠GHI
Answer:
Always true because ∠GHI corresponds to ∠ABC in the original drawing, and angle measures are preserved in scale drawings.
C. \(\frac{A B}{G H}=\frac{B C}{H I}\)
Answer:
Always true because distances in a scale drawing are equal to their corresponding distances in the original drawing times the scale factor r, so \(\frac{A B}{G H}=\frac{A B}{r(A B)}=\frac{1}{r}\) and \(\frac{B C}{H I}=\frac{B C}{r(B C)}=\frac{1}{r}\).
d. Perimeter (GHIJ) = r ∙ Perimeter(ABCD)
Answer:
Always true because the distances In a scale drawing are equal to their corresponding distances in the original
drawing times the scale factor r, so
Perimeter(GHIJ) = GH + HI + iJ +1G
Perimeter(GHIJ) = r(AB) + r(BC) + r(CD) + r(DA)
Perimeter(GHJJ) = r(AB + BC + CD + DA)
Perimeter(GHIJ) = r Perimeter(ABCD).
e. Area (GHIJ) = r ∙ Area(ABCD) where r ≠ 1
Answer:
Never true because the area of a scale drawing is related to the area of the original drawing by the factor r2.
The scale factor r > 0 and r ≠ 1, so r ≠ r2.
f. r < 0
Answer:
Never true in a scale drawing because any distance in the scale drawing would be negative as a result of the scale factor and, thus, cannot be drawn since distance must always be positive.
Eureka Math Geometry Module 2 Lesson 1 Exit Ticket Answer Key
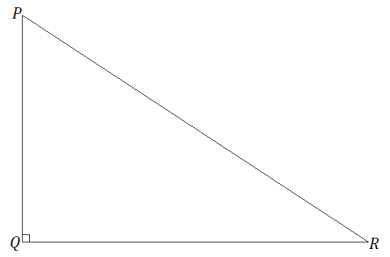
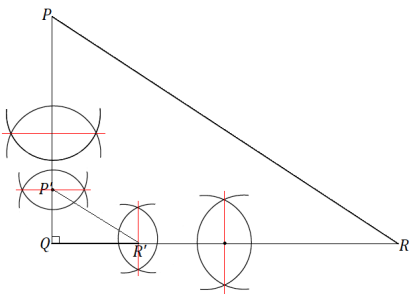
Triangle ABC is provided below, and one side of scale drawing ∆ A’B’C’ is also provided. Use construction tools to complete the scale drawing and determine the scale factor. What properties do the scale drawing and the original figure share? Explain how you know.
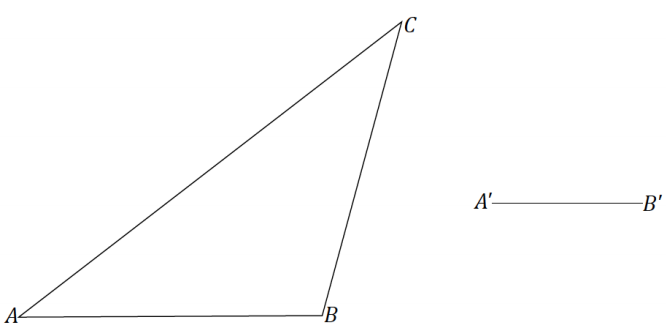
Answer:
One possible solution: Since the scale drawing will clearly be a reduction, use the compass to mark the number of lengths equal to the length of \(\overline{A^{\prime} B^{\prime}}\) along \(\overline{A B}\). Once the length of \(\overline{A^{\prime} C^{\prime}}\) is determined to be \(\frac{1}{2}\) the length of \(\overline{A B}\), use the compass to find a length that is half the length of \(\overline{A B}\) and half the length of \(\overline{B C}\). Construct circles with radii of lengths \(\frac{1}{2}\) AC and \(\frac{1}{2}\) BC
from the A’ and B’, respectively, to determine the location of C’, which is at the intersection of the two circles.
By measurement, I can see that each side is \(\frac{1}{2}\) the length of the corresponding side of the original figure and that all three angles are equal in measurement to the three corresponding angles in the original figure.