Eureka Math Geometry Module 3 Lesson 13 Answer Key

Engage NY Eureka Math Geometry Module 3 Lesson 13 Answer Key

Eureka Math Geometry Module 3 Lesson 13 Example Answer Key

Let us now try drawing cross-sections of an everyday object, such as a coffee cup.
$Eureka Math Geometry Module 3 Lesson 13 Example Answer Key 1$

Sketch the cross-sections at each of the indicated heights.
$Eureka Math Geometry Module 3 Lesson 13 Example Answer Key 2$
Answer:
$Eureka Math Geometry Module 3 Lesson 13 Example Answer Key 3$

Eureka Math Geometry Module 3 Lesson 13 Opening Exercise Answer Key

a. Observe the following right circular cone. The base of the cone lies in plane S, and planes P, Q, and R are all parallel to S. Plane P contains the vertex of the cone.
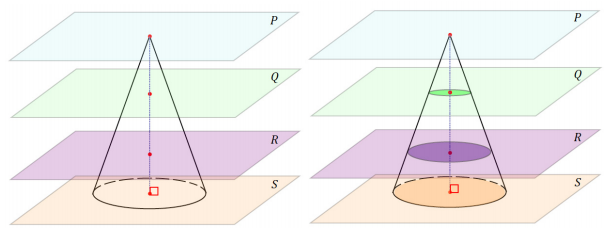
$Eureka Math Geometry Module 3 Lesson 13 Opening Exercise Answer Key 4$
$Eureka Math Geometry Module 3 Lesson 13 Opening Exercise Answer Key 5$
Answer:
$Eureka Math Geometry Module 3 Lesson 13 Opening Exercise Answer Key 6$

b. What happens to the cross-sections as we look at them starting with P’ and working toward S’?
Answer:
The intersection of plane P with the cone is a point, and each successive cross-section is a disk of greater radius than the previous disk.

Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key

Exercise 1.
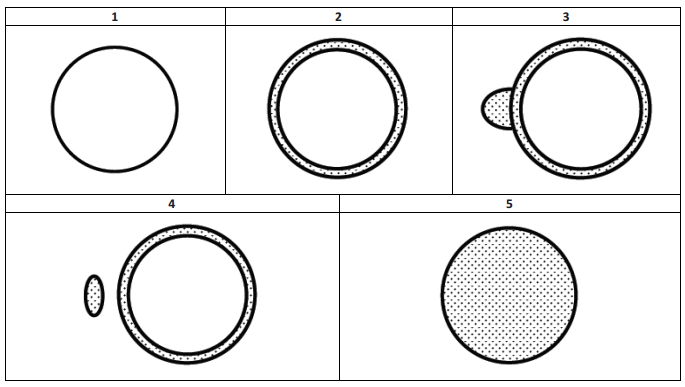
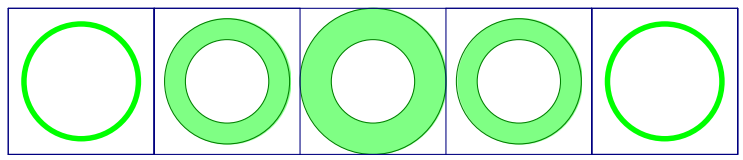
Sketch five evenly spaced, horizontal cross-sections made with the following figure.
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 7$
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 8$
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 10$
Answer:
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 10$

Exercise 2.
A cone with a radius of 5 cm and height of 8 cm is to be printed from a 3D printer. The medium that the printer will use to print (i.e., the “ink” of this 3D printer) is a type of plastic that comes In coils of tubing that has a radius of 1$\frac{1}{3}$ cm. What length of tubing is needed to complete the printing of this cone?
Answer:
The volume of medium used (contained in a circular cylinder) must be equal to the volume of the cone being printed.
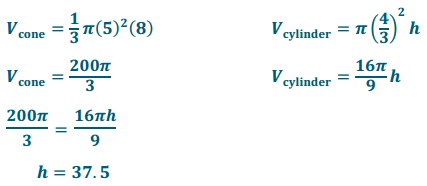
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 11$
The cone will require 37.5 cm of tubing.

Exercise 3.
A cylindrical dessert 8 cm in diameter is to be created using a type of 3D printer specially designed for gourmet kitchens. The printer will “pipe” or, in other words, “print out” the delicious filling of the dessert as a solid cylinder. Each dessert requires 300 cm3 of filling. Approximately how many layers does each dessert have if each layer is 3 mm thick?
Answer:
Volume = πr²h
300 = π(4)²h
$\frac{300}{16 \pi}$ = h
h ≈ 5.968
The total height of the dessert is approximately 6 cm. Since each layer is 3 mm (or 0.3 cm) thick,
height = (thickness of layer) × (number of layers)
$\frac{300}{16 \pi}$ = (0. 3)n
n ≈ 19.89.
Each dessert has about 20 layers.

Exercise 4.
The image shown to the right Is of a fine tube that is printed from a 3D printer that prints replacement parts. If each layer is 2 mm thick, and the printer prints at a rate of roughly 1 layer In 3 seconds, how many minutes will it take to print the tube?
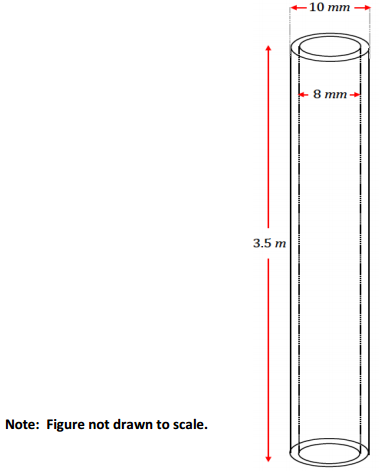
$Eureka Math Geometry Module 3 Lesson 13 Exercise Answer Key 12$
Answer:
The printer prints at a rate of $\frac{1}{3}$ layers per second. The total height of the tube is 3.5 m, or 350 cm. If each layer is 2 mm, or 0.2 cm thick, then the tube has a total of 1,750 layers.
distance = rate × time
1750 = $\frac{1}{3}$(t)
t = 5250
The time to print the tube is 5,250 seconds, or 87.5 minutes.

Eureka Math Geometry Module 3 Lesson 13 Problem Set Answer Key

Question 1.
Horizontal slices of a solid are shown at various levels arranged from highest to lowest. What could the solid be?
$Eureka Math Geometry Module 3 Lesson 13 Problem Set Answer Key 13$
Answer:
Answers vary. The solid could be a ball with a hole in it.

Question 2.
Explain the difference in a 3D printing of the ring pictured in Figure 1 and Figure 2 if the ring is oriented in each of the following ways.
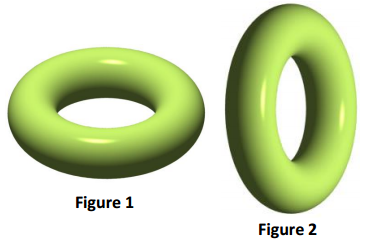
$Eureka Math Geometry Module 3 Lesson 13 Problem Set Answer Key 14$
Answer:
For the first ring, the cross-sections are circles or regions between concentric circles. For the second ring, the cross- sections are stretched cirles and then two separated regions.

Question 3.
Each bangle printed by a 3D printer has a mass of exactly 25 g of metal. If the density of the metal is 14 g/cm³, what length of a wire 1 mm in radius is needed to produce each bangle? Find your answer to the tenths place.
Answer:
Radius of filament: 1 mm = 0. 1 cm
Volume_bangle = π(0. 1)²(h) = 0.01πh
14 = $\frac{25}{0.01 \pi h}$
h ≈ 56.8
The wire must be a length of 56.8 cm.

Question 4.
A certain 3D printer uses 100 m of plastic filament that is 1. 75 mm in diameter to make a cup. If the filament has a density of 0.32 g/cm³, find the mass of the cup to the tenths place.
Answer:
Length of filament: 100 m = 10⁴ cm
Radius of filament: 0.875 mm = 0.0875 cm
Volume_filament = π(0.0875)²(10⁴) = 76.5625π
Mass of cup: (76.5625π cm³)(0. 32 g/cm³) = 24. 5π g
The mass of the cup is approximately 77 g.

Question 5.
When producing a circular cone or a hemisphere with a 3D printer, the radius of each layer of printed material must change in order to form the correct figure. Describe how the radius must change in consecutive layers of each figure.
Answer:
The slanted side of a circular cone can be modeled with a sloped line in two dimensions, so the change in radius of consecutive layers must be constant; i.e., the radius of each consecutive layer of a circular cone decreases by a constant C.

The hemisphere does not have the same profile as the cone. In two dimensions, the profile of the hemisphere cannot be modeled by a line but, rather, an arc of a circle, or a semicircle. This means that the change in radius between consecutive layers of print material is not constant. In fact, if printing from the base of the hemisphere, the change in radius must start out very close to 0, and then increase as the printer approaches the top of the hemisphere, which is a point that we can think of as a circle of radius 0.

Question 6.
Suppose you want to make a 3D printing of a cone. What difference does it make If the vertex is at the top or at the bottom? Assume that the 3D printer places each new layer on top of the previous layer.
Answer:
If the vertex is at the top, new layers will always be supported by old layers. If the vertex is at the bottom, new layers will hang over previous layers.

Question 7.
Filament for 3D printing Is sold in spools that contain something shaped like a wire of diameter 3 mm. John wants to make 3D printings of a cone with radius 2 cm and height 3 cm. The length of the filament is 25 meters. About how many cones can John make?
Answer:
The volume of the cone is V = $\frac{1}{3}$π(2 cm)² · 3 cm = 4π cm³.
The volume of the filament is V = 2500 cm · π · 0.15² cm² = 56.25π cm³.
Since 56.25π cm³ ÷ 4π cm³ = 14.0625, John can make 14 cones as long as each 3D-printed cone has volume no more than 4π cm³.

Question 8.
John has been printing solid cones but would like to be able to produce more cones per each length of filament than you calculated in Problem 7. Without changing the outside dimensions of his cones, what is one way that he could make a length of filament last longer? Sketch a diagram of your idea, and determine how much filament John would save per piece. Then, determine how many cones John could produce from a single length of filament based on your design.
Answer:
Students’ answers vary. One possible solution would be to print only the outer shell of the cone, leaving a hollow center in the shape of a scaled-down cone. Something that students may consider in their solution is the thickness of the wall of the shell and the integrity of the final product. This would provide a variety of answers.

Question 9.
A 3D printer uses one spool of filament to produce 20 congruent solids. Suppose you want to produce similar solids that are 10% longer in each dimension. How many such figures could one spool of filament produce?
Answer:
Each new solid would have volume 1.331 times the volume of an original solid. Let x be the number of new figures produced. Then, 1. 331x = 20 and x = $\frac{20}{1.331}$ ≈ 15.03.
It should be possible to print 15 of the larger solids.

Question 10.
A fabrication company 3D-prints parts shaped like a pyramid with base as shown In the following figure. Each pyramid has a height of 3 cm. The printer uses a wire with a density of 12 g/cm³ at a cost of $0. 07/g.

It costs $500 to set up for a production run, no matter how many parts they make. If they can only charge $15 per part, how many do they need to make in a production run to turn a profit?
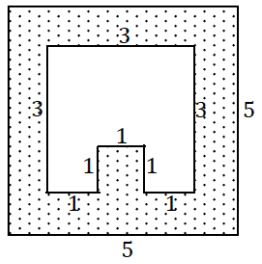
$Eureka Math Geometry Module 3 Lesson 13 Problem Set Answer Key 15$
Answer:
Volume of a single part:
V = $\frac{1}{3}$Bh
V = $\frac{1}{3}$(17)(3)
V = 17; the volume of each part is 17 cm³.

Mass of a single part
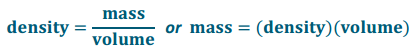
$Eureka Math Geometry Module 3 Lesson 13 Problem Set Answer Key 16$
mass = (12)(17)
mass = 204
The mass of a single part is 204 g.

Cost of a single part:
cost = (204)(0.07)
cost = (204)(0.07)
cost = 14.28
The cost of a single part is $14.28.
The sum of the production run cost and the cost to make the total number of parts must be less than the product of the price and the total number of parts. Let n be the total number of parts:
500 + 14.28n < 15n
500 < 0.72n n > 694.4̅.
Therefore, in order to turn a profit, 695 parts must be made in a production run.

Eureka Math Geometry Module 3 Lesson 13 Exit Ticket Answer Key

Lamar is using a 3D printer to construct a circular cone that has a base with radius 6 in.

a. If his 3D printer prints in layers that are 0. 004 in. thick (similar to what is shown in the image below), what should be the change in radius for each layer in order to construct a cone with height 4 in.?
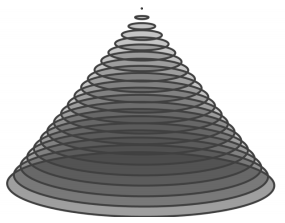
$Eureka Math Geometry Module 3 Lesson 13 Exit Ticket Answer Key 17$
Answer:
$\frac{4}{6}=\frac{3.996}{x}$
x = 5.994
6 – 5.994 = 0.006
The change in radius between consecutive layers is 0.006 inch.

b. What is the area of the base of the 27th layer?
Answer:
The 27^th layer of the cone will have a radius reduced by 0.006 inch 26 times.
26(0.006) = 0.156
6 – 0.156 = 5.844
The radius of the 27^th layer is 5.844 in.
A = π(5. 844)²
A ≈ 107.3
The area of the base of the disk in the 27^th layer is approximately 107.3 in².

c. Approximately how much printing material is required to produce the cone?
Answer:
The volume of printing material is approximately equal to the volume of a true cone with the same dimensions.
V = $\frac{1}{3}$π(6)² (4)
V = 48π
Approximately 150.8 in³ of printing material is required.