Engage NY Eureka Math Algebra 2 Module 3 Mid Module Assessment Answer Key
Eureka Math Algebra 2 Module 3 Mid Module Assessment Answer Key
Question 1.
Use properties of exponents to explain why it makes sense to define 16\(\frac{1}{4}\) as \(\sqrt[4]{16}\).
Answer:
(16\(\frac{1}{4}\))4 = 16\(\frac{1}{4}\) . 16\(\frac{1}{4}\) . 16\(\frac{1}{4}\) . \(\frac{1}{4}\) = 161 = 16
Question 2.
Use properties of exponents to rewrite each expression as either an integer or as a quotient of integers \(\frac{p}{q}\) to show the expression is a rational number.
a. \(\sqrt[4]{2} \sqrt[4]{8}\)
Answer:
\(\sqrt[4]{2} \sqrt[4]{8}\) = 2\(\frac{1}{4}\) . 8\(\frac{1}{4}\) = 2\(\frac{1}{4}\) .(23)\(\frac{1}{4}\) = 2\(\frac{1}{4}\) . 2\(\frac{3}{4}\) = \(2^{\frac{1}{4}+\frac{3}{4}}\) = 21
Thus, \(\sqrt[4]{2} \sqrt[4]{8}\) = 2 is a rational number.
b. \(\frac{\sqrt[3]{54}}{\sqrt[3]{2}}\)
Answer:
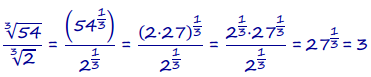
Thus, \(\frac{\sqrt[3]{54}}{\sqrt[3]{2}}\) = 3 is a rational number.
c. 16<sup>\(\frac{2}{3}\)</sup> . \(\left(\frac{1}{27}\right)^{\frac{2}{3}}\)
Answer:
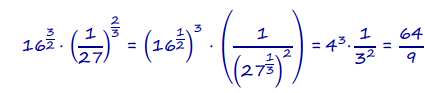
Thus, 16<sup>\(\frac{2}{3}\)</sup> . \(\left(\frac{1}{27}\right)^{\frac{2}{3}}\) = \(\frac{64}{9}\) is a rational number.
Question 3.
Use properties of exponents to rewrite each expression with only positive, rational exponents. Then find the numerical value of each expression when x = 9, y = 8, and z = 16. In each case, the expression evaluates to a rational number.
a. \(\sqrt{\frac{x y^{2}}{\left(x^{3} z\right)^{\frac{1}{2}}}}\)
Answer:
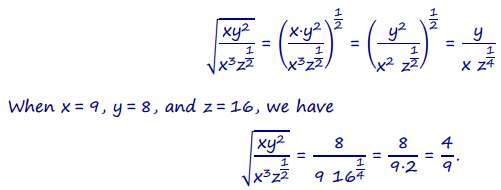
b. \(\sqrt[11]{y^{2} Z^{4}}\)
Answer:
\(\sqrt[11]{y^{2} Z^{4}}\) = \(\left(y^{2} z^{4}\right)^{\frac{1}{11}}=\frac{2}{y^{11}} z^{\frac{4}{11}}\)
when y = 8 and z = 16, we have
\(\sqrt[11]{y^{2} Z^{4}}\) = 8\(\frac{2}{11}\) . 16\(\frac{4}{11}\) = (23)\(\frac{2}{11}\) . (24)\(\frac{4}{11}\) = 2\(\frac{6}{11}\) . 2\(\frac{16}{11}\) = 2\(\frac{22}{11}\) = 22 = 4
c. x<sup>\(-\frac{3}{2}\)</sup> y<sup>\(\frac{4}{3}\)</sup> z<sup>\(-\frac{3}{4}\)</sup>
Answer:
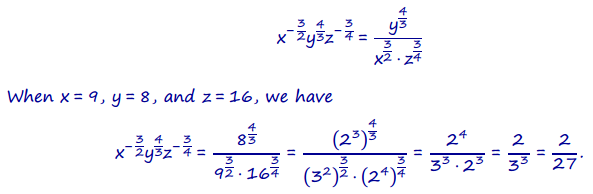
Question 4.
We can use finite approximations of the decimal expansion of ir = 3.141519 … to find an approximat value of the number 3π.
a. Fill in the missing exponents in the following sequence of inequalities that represents the recursi process of finding the value of 3π:

Answer:

b. Explain how this recursive process leads to better and better approximations of the number 3π.
Answer:
We can get better and better approximates of π by squeezing it between rational under and overestimates that use more and more digits of its decimal expansion.
3 < π< 4
3.1 < π < 3.2
3.14< π < 3.15
.
.
.
Ther, we can estimate 3π by sqeezing it between expressions with rational exponents.
Because we know how to calculate a number such as 33.14 = 33 . 30.14 =27\(\left(\sqrt[100]{3^{14}}\right)\) we have a method for calculating the urder and over estimates of 3π.
Because 3 < π < 4, we have 33 < 3π < 34. Thus, 27 < 3π < 81
Because 3.1 < π < 3.2, we have 33.1 < 3π < 33.2 Thus, 30.1353 < 3π < 33.6347.
Because 3.14 < π < 3.15, we have 33.14 < 3π < 33.15 Thus, 31.4891 < 3π < 31.8370. continuing this process, we can approximate 3π as closely as we want by starting with more and more digits of π in the exponent.
Question 5.
A scientist is studying the growth of a population of bacteria. At the beginning of her study, she has 800 bacteria. She notices that the population is quadrupling every hour.
a. What quantities, including units, need to be identified to further investigate the growth of this bacteria population?
Answer:
we need to know the initial population, P0, in either units of single bacteria or hundreds of bacteria, the time, t, in hours, and the current population, P(t) at time t, in the same units as the initial population P0.
b. The scientist recorded the following information in her notebook, but she forgot to label each row. Label each row to show what quantities, including appropriate units, are represented by the numbers in the table, and then complete the table.

Answer:

c. Write an explicit formula for the number of bacteria present after t hours.
Answer:
After t hours, there are P(t) = 8(4t) hundred bacteria present. (It is also acceptable to model this population by P(t) = 800(4t) single bacteria).
d. Another scientist studying the same population notices that the population is doubling every half an hour. Complete the table, and write an explicit formula for the number of bacteria present after x half hours.

Answer:
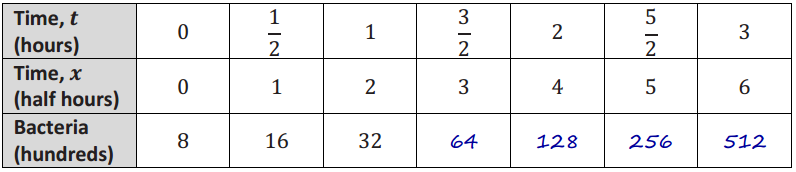
After x half hours, there are Q(x) = 8(2x) hundred bacteria present. (It is also acceptable to model this population by Q(x) = 8–(2x) single bacteria.
e. Find the time, in hours, when there will be 5,120,000 bacteria. Express your answer as a logarithmic expression.
Answer:
Students may choose to use the base – 2 formula but will need to adjust the value of x, which counts half hours, to t, which counts full hours, to correctly answer the question. Also, note the 5,120,000 is 51,200 hundred bacteria, so if students modeled the population using bacteria instead of hundreds, they should solve 800(4t) = 5,120,000. Students may also solve this equation using base – 4 logarithms or base – 2 logarithms, giving an equivalent solution that looks different.
8(4t) = 51200
4t = 6400
tlog(4) = log(6400)
t = \(\frac{\log (6400)}{\log (4)}\)
f. A scientist calculated the average rate of change for the bacteria in the first three hours to be 168. Which units should the scientist use when reporting this number? Explain how you know.
Answer:
The average rate of change over the first three hours is given by the expression \(\frac{P(3)-P(O)}{3-0}\), which is a quotient of the number of bacteria in hundreds per hour. Thus, the unit should be reported as hundreds of bacteria per hour. Note that if students had modeled the population using single bacteria instead of hundreds, they should answer that the units are in bacteria per hour.
Question 6.
Solve each equation. Express your answer as a logarithm, and then approximate the solution to the nearest thousandth.
a. 3(10)-x = \(\frac{1}{9}\)
Answer:
3(10)-x = \(\frac{1}{9}\)
\(\frac{1}{10^{x}}=\frac{1}{27}\)
10x = 27
x = log(27)
x ≈ 1.431
b. 362(10\(\frac{t}{12}\)) = 500
Answer:
362(10\(\frac{t}{12}\)) = 500
\(10^{\frac{t}{12}}=\frac{500}{362}\)
\(\frac{t}{12}=\log \left(\frac{500}{362}\right)\)
t ≈ 1.683
c. (2)3x = 9
Answer:
(2)3x = 9
log2(23x) = log2(9)
3x = log2(9)
x = \(\frac{1}{3}\)log2(9) = \(\frac{1}{3} \frac{\log (9)}{\log (2)}\)
x ≈ 1.057
d. 300e0.4t = 900
Answer:
300e0.4t = 900
e0.4t = 3
ln(e0.4t) = ln(3)
0.4t = 3
t = 2.5ln(3)
t ≈ 2.747
Question 7.
Because atoms, molecules, and ions are very small, they are counted in units of moles, where 1 mole = 6.022 × 1023 molecules. Concentration of ions in a liquid is measured in units of moles per liter. The measure of the acidity of a liquid is called the pH of the liquid and is given by the formula pH = -log(H),
where H is the concentration of hydrogen ions in units of moles per liter.
a. Water has a pH value of 7.0. How many hydrogen ions are in one liter of water
Answer:
7 = -log(H)
-7 = log(H)
H = 10-7
Thus, there are approximately 10-7 moles of hydrogen in one liter of water. If we multiply this by 6.023 × 1023 ions per mole, we find that there are 6.022 × 1016 hydrogen ions.
b. If a liquid has a pH value larger than 7.0, does one liter of that liquid contain more or fewer hydrogen ions than one liter of water? Explain.
Answer:
A liquid with a PH value larger than 7.0 will contain fewer hydrogen ions than one liter of water because H = \(\frac{1}{10^{p H}}\), and when the PH is larger than 7.0, the value of H will become smaller because the quantities H and 10pH are inversely population to one another.
c. Suppose that liquid A is more acidic than liquid B, and their pH values differ by 1.2. What is the ratio of the concentration of hydrogen ions in liquid A to the concentration of hydrogen ions in liquid B?
Answer:
Let HA be the concentration of hydrogen ions in liquid A, and let HB be the concentration of hydrogen ions in liquid B. Then, the difference of PH values is -(-log(HB)) – (-log(HA)) = 1.2. Solve this equation \(\frac{\mathrm{H}_{\mathrm{A}}}{\mathrm{H}_{B}}\), the requested ratio.
-log(HB) + log(HA) = 1.2
log(\(\frac{\mathrm{H}_{\mathrm{A}}}{\mathrm{H}_{B}}\)) = 1.2
\(\frac{\mathrm{H}_{\mathrm{A}}}{\mathrm{H}_{B}}\) = 101.2 = 15.85
Question 8.
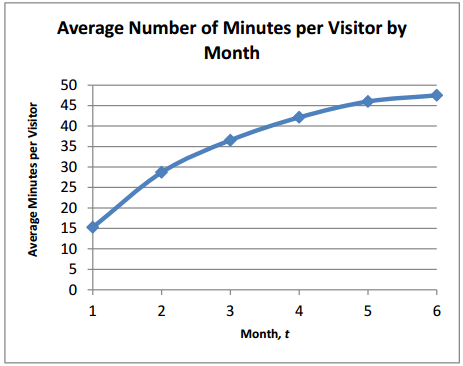
A social media site is experiencing rapid growth. The table below shows the number of unique visitors, V, in month t for a 6-month period of time. The graph shows the average minutes per visit to the site, M, in each month, t, for the same 6-month period of time.

a. Between which two months did the site experience the most growth in total unique visitors? What is the average rate of change over this time interval?
Answer:
V(2) – V(1) = 190000
V(3) – V(2) = 423000
V(4) – V(3) = 239000
V(5) – V(4) = 753000
V(6) – V(5) =1272000
The largest growth in the number of visitors occurs between months 5 and 6.
b. Compute the value of \(\frac{V(6)-V(1)}{6-1}\), and explain its meaning in this situation.
Answer:
\(\frac{V(6)-V(1)}{6-1}=\frac{3295000-418000}{5}\) = 575400
This means that the average monthly growth of visitors to the site between months 1 and 6 is 575,400 visitors per month.
c. Between which two months did the average length of a visit change by the least amount? Estimate the average rate of change over this time interval.
Answer:
The two neighbouring points that have the closest y – values are in months 5 and 6. Estimating values M(6) ≈ 47.5 and M(5) ≈ 46 from the graph, we see that the average rate of change over this interval is \(\frac{M(6)-M(5)}{6-5}=\frac{47.5-46}{1}\) = 1.5 minutes per visitor per month.(Students may read different values from the graph.)
d. Estimate the value of \(\frac{M(3)-M(2)}{3-2}\) from the graph of M, and explain its meaning in this situation.
Answer:
Estimating values M(3) ≈ 37 and M(2) ≈ 28 from the graph, we have \(\frac{M(3)-M(2)}{3-2}=\frac{37-28}{1}\) = 9, meaning that on average , each visit to the website increased by 9 minutes between months 2 and 3.
e. Based on the patterns they see in the table, the company predicts that the number of unique visitors will double each month after the sixth month. If growth continues at this pace, when will the number of unique visitors reach 1 billion?
Answer:
3295000(2)t = 1000000000
2t = 303.49
log(2t) = log(303.49)
t log(2) = log(303.49)
t = \(\frac{\log (303.49)}{\log (2)}\)
t ≈ 8.25
If growth continues at this pace, the number of unique visitors will reach 1 billion after 8.25 additional months have passed.