Engage NY Eureka Math Algebra 2 Module 3 End of Module Assessment Answer Key
Eureka Math Algebra 2 Module 3 End of Module Assessment Answer Key
Question 1.
For parts (a) to (c),
Sketch the graph of each pair of functions on the same coordinate axes showing end behavior and intercepts, and
Describe the graph of g as a series of transformations of the graph of f.
a. f(x) = 2x and g(x) = 2-x + 3
Answer:
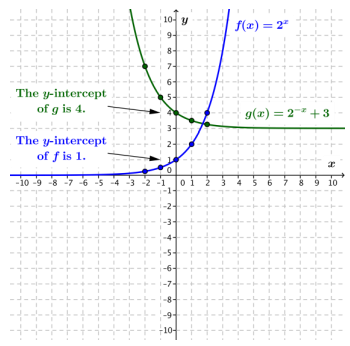
The graph of g is the graph of f reflected across y-axis and translated vertically 3 units.
b. f(x) = 3x, and g(x) = 9x – 2
Answer:
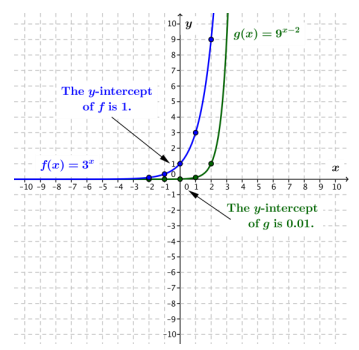
Answers will vary. For example, because 9x – 2 = 32(x – 2), the graph of g is the graph of f scaled horizontally by a factor of \(\frac{1}{2}\) and translated horizintally by 2 units to the right.
c. f(x) = log2(x), and g(x) = log2((x – 1)3)
Answer:
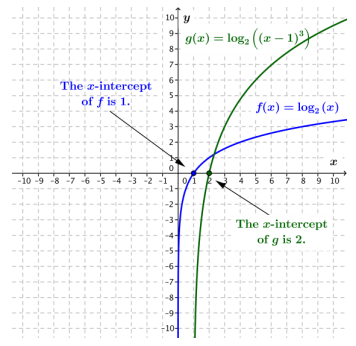
Most likely answer: Because log2((x – 1)3) = 3 log2(x – 1), the graph of g is the graph of f scaled vertically by a factor of 3 and translated horizontally by 1 unit to the right.
Question 2.
consider the gaph of f(x) = 8x. Let g(x) = f(\(\frac{1}{3}\)x + \(\frac{2}{3}\)) and h(x) = 4f(\(\frac{x}{3}\))
a.Describe the graphs of g and h as transformations of the graph of f.
Answer:
The graph of g is the graph of f with a horizontal scaling by a factor of 3 and a horizontal translation 2 units to the left. The graph of h is the graph of f scaled vertically by a factor of 4 and horizontally by a factor of 3.
b. the properties of exponents to show why the graphs of the functions g(x) = f(\(\frac{1}{3}\)x + \(\frac{2}{3}\)) and h(x) = 4f(\(\frac{x}{3}\)) are the same.
Answer:
Since g(x) = 8\(\frac{x}{3}\) + \(\frac{2}{3}\), h(x) = 4 . 8\(\frac{x}{3}\), 8\(\frac{x}{3}\) + \(\frac{2}{3}\) = 8\(\frac{2}{3}\) = 4 . 8\(\frac{x}{3}\) for any real number x, and their domains are the same, the functions g and h are equivalent. Therefore, they have identical graphs
Question 3.
The graphs of the functions f(x) = ln(x) and g(x) = log2(x) are shown to the right.
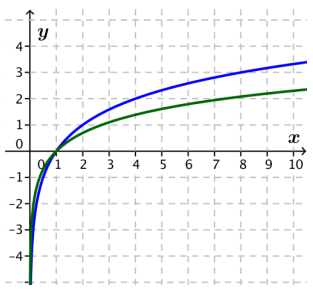
a. Which curve is the graph of f, and which curve is the graph of g? Explain.
Answer:
The blue curve on top is the graph of g, and the green curve on the bottom is the graph of f. The two functions can be compared by converting both of them to the same base. Since f(x) = ln(x), and g(x) = \(\frac{1}{\ln (2)}\) . ln(x), and 1 < \(\frac{1}{\ln (2)}\), the graph of g is a vertical stretch of the graph of f; thus, the graph of g is the blue curve.
b. Describe the graph of g as a transformation of the graph of f.
Answer:
The graph of g is a vertical scaling of the graph of f by a scale factor greater than one.
c. By what factor has the graph of f been scaled vertically to produce the graph of g? Explain how you know.
Answer:
By the change of base formula, g(x) = \(\frac{1}{\ln (2)}\) . ln(x); thus, the graph of g is a vertical scaling of the graph of f by a scale factor of \(\frac{1}{\ln (2)}\).
Question 4.
Gwyneth is conducting an experiment. She rolls 1,000 dice simultaneously and removes any that have a six showing. She then rerolls all of the dice that remain and again removes any that have a six showing. Gwyneth does this over and over again—rerolling the remaining dice and then removing those that land with a six showing.
a. Write an exponential function f of the form f(n) = a bC for any real number n ≥ 0 that could be used to model the average number of dice she could expect on the n roll if she ran her experiment a large number of times.
Answer:
f(n) = 1000(\(\frac{5}{6}\))n
b. Gwyneth computed f(12) = 112.15… using the function f. How should she interpret the number 112.15… in the context of the experiment?
Answer:
The value f(12) = 112.15 means that if she was to run her experiment over and over again, the model predicts that the average number of dice left after the 12th roll would be approximately 112.15.
c. Explain the meaning of the parameters in your function f in terms of this experiment.
Answer:
The number 1,000 represents the initial amount of dice. The number \(\frac{5}{6}\) represents the
fraction of dice remaining from the previous roll each time she rolls the dice; there is a \(\frac{5}{6}\) probability that any die will not land on a 6, so we would predict that after each roll about \(\frac{5}{6}\) of the dice would remain.
d. Describe in words the key features of the graph of the function f for n ≥ 0. Be sure to describe where the function is increasing or decreasing, where it has maximums and minimums (if they exist), and the end behavior.
Answer:
This function is decreasing for all n ≥ 0. The maximum is the starting number of dice, 1,000. There is no minimum. The graph decreases at a decreasing rate with f(x) → 0 as x → ∞.
e. According to the model, on which roll does Gwyneth expect, on average, to find herself with only one die remaining? Write and solve an equation to support your answer to this question.
Answer:
1000(\(\frac{5}{6}\))n = 1
(\(\frac{5}{6}\))n = \(\frac{1}{1000}\)
log(\(\frac{5}{6}\)|)n = log(\(\frac{1}{1000}\))
n log(\(\frac{5}{6}\)) = -3
n = –\(\frac{3}{\log \left(\frac{5}{6}\right)}\)
n ≈ 37.89
According to the model, Gwyneth should have 1 die remaining, on average, on the 38th roll.
f. For all of the values in the domain of f, is there any value for which f will predict an average number of 0 dice remaining? Explain why or why not. Be sure to use the domain of the function and the graph to support your reasoning.
Answer:
The graph of this function shows the end behavior approaching 0 as the number of rolls increases. This function will never predict an average number of0 dice remaining because a function of the form f(n) = abcn never takes on the value of zero. Even as the number of trials becomes very large, the value of f will be a positive number.
Suppose the table below represents the results of one trial of Gwyneth’s experiment.
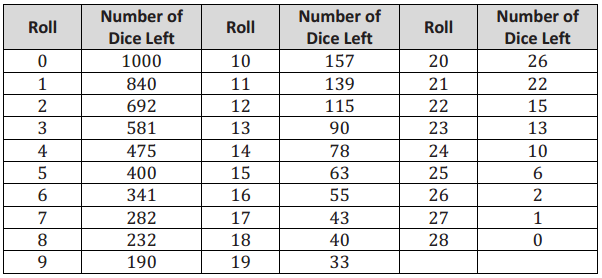
g. Let g be the function that is defined exactly by the data in the table (i.e., g(0) = 1000, g(1) = 840, g(2) = 692, and so forth, up to g(28) = 0). Describe in words how the graph of g looks different from the graph off. Be sure to use the domain of g and the domain of f to justify your description.
Answer:
The domain of g is the set of integers from 0 to 28. The graph of g is discrete (a set of unconnected points), while the graph of f is continuous (a curve). The graph of g has an x-intercept at (28, 0), and the graph of f has no x-intercept. The graphs of both functions decrease, but the graph of f is exponential, which means that the ratio \(\frac{f(x+1)}{f(x)}=\frac{5}{6}\) for all x in the domain of f. The function values for g do not have this property.
h. Gwyneth runs her experiment hundreds of times, and each time she generates a table like the one in part (f). How are these tables similar to the function f? How are they different?
Answer:
Similar:
The data in each table will follow the same basic pattern as f (i.e., decreasing from 1,000 eventually to 0 with a common ratio between rolls of about \(\frac{5}{6}\)).
Different:
(1) The tables are always discrete domains with integer range. (2) Each table will eventually reach 0 after some finite number of rolls, whereas the function g can never take on the value of 0.
Question 5.
Find the inverse g for each function f.
a. f(x) = \(\frac{1}{2}\)x – 3
Answer:
y = \(\frac{1}{2}\)x – 3
x = \(\frac{1}{2}\)y – 3
x + 3 = \(\frac{1}{2}\)y
y = 2x + 6
g(x) = 2x + 6
b. f(x) = \(\frac{x+3}{x-2}\)
Answer:
y = \(\frac{x+3}{x-2}\)
x = \(\frac{y+3}{y-2}\)
xy -2x = y + 3
y(x – 1) = 2x + 3
y = \(\frac{2 x+3}{x-1}\)
g(x) = \(\frac{2 x+3}{x-1}\)
c. f(x) = 23x + 1
Answer:
y = 23x + 1
x = 23y + 1
x – 1 = 23y
log<sub>2</sub>(x – 1) = 3y
y = \(\frac{1}{3}\) log2(x – 1)
g(x) = \(\frac{1}{3}\) log2(x – 1)
d. f(x) = ex – 3
Answer:
y = ex – 3
x = ey – 3
ln(x) = y – 3
y = ln(x) + 3
g(x) = ln(x) + 3
e. f(x) = log(2x + 3)
Answer:
y = log(2x + 3)
x = log(2y + 3)
2y + 3 = 10x
y = \(\frac{1}{2}\) . 10x – \(\frac{3}{2}\)
g(x) = \(\frac{1}{2}\) . 10x – \(\frac{3}{2}\)
Question 6.
Dani has $1,000 in an investment account that earns 3% per year, compounded monthly.
a. Write a recursive sequence for the amount of money in her account after n months.
Answer:
a1 = 1000, an + 1 = an(1.0025)
b. Write an explicit formula for the amount of money in the account after n months.
Answer:
an= 1000(1.0025)n
c. Write an explicit formula for the amount of money in her account after t years.
Answer:
b(t) = 1000(1.0025)12t
d. Boris also has $1,000, but in an account that earns 3% per year, compounded yearly. Write an explicit formula for the amount of money in his account after t years.
Answer:
V(t) = 1000(1.03)t
e. Boris claims that the equivalent monthly interest rate for his account would be the same as Dani’s. Use the expression you wrote in part (d) and the properties of exponents to show why Boris is incorrect.
Answer:
Boris is incorrect because the formula for the amount of money in the account, based on a monthly rate, is given by V(t) = 1000(1+ i)12t, where i is the monthly interest rate. The expression from part d, 1000(1.03)t, is equivalent to 1000(1.03)\(\frac{12t}{12}\) = 1000(1.03)\(\frac{1}{12}\) .12t = 1000((1.03)\(\frac{1}{12}\))12t by properties of exponents. Therefore, if the expressions must be equivalent, the quantity given by 1.03\(\frac{1}{12}\) ≈ 1.00247 means that his monthly rate is about 0.247%, which is less than 0.25%, given by Dani’s formula.
Question 7.
Show that \(\sum_{k=0}^{n-1}\)a. rk = a\(\left(\frac{1-r^{n}}{1-r}\right)\) where r ≠ 1.
Answer:
We recall the identity 1 – rn = (1 – r)(1 + r + r2 + r3 + ….. + rn – 1) with r ≠ 1 and positive integer n. Dividing both sides of the identity by 1 – r gives
\(\frac{1-r^{n}}{1-r}\) = 1 + r + r2 + r3 + ….. + rn – 1
Therefore, by factoring the common factor a and substituting, we get the formula,
a + ar + ar2 + ….. + arn – 1 = a(1 + r + r2 + …. + rn – 1)
= a\(\frac{1-r^{n}}{1-r}\)
Question 8.
Sami opens an account and deposits $100 into it at the end of each month. The account earns 2% per year compounded monthly. Let S, denote the amount of money in her account at the end of n months (just after she makes a deposit). For example, S1 = 100 and S2 = 100 (1 + \(\frac{0.01}{12}\)) + 100.
a. Write a geometric series for the amount of money in the account after 3, 4, and 5 months.
Answer:

b. Find a recursive description for Sn.
Answer:
S1= 100, Sn = Sn – 1(1 + \(\frac{0.02}{12}\)) + 100
c. Find an explicit function for Sn, and use it to find S12.
Answer:
Sn = \(\frac{100\left(1-\left(1+\frac{0.02}{12}\right)^{n}\right)}{1-\left(1+\frac{0.02}{12}\right)}\)
S12 ≈ 1211.06
d. When will Sami have at least $5,000 in her account? Show work to support your answer.
Answer:
An algebraic solution is shown, but students could also solve this equation numerically.
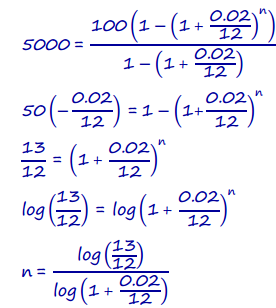
The solution is approximately 48.07. At the end of the 49th month, she will have over $5000 in her account. It will take about 4 years and 2 days.
Question 9.
Beatrice decides to deposit $100 per month at the end of every month in a bank with an annual interest rate of 5.5% compounded monthly.
a. Write a geometric series to show how much she will accumulate in her account after one year.
Answer:
100(1 + \(\frac{0.055}{12}\))12 + 100(1 + \(\frac{0.055}{12}\))11 + …. + 100(1 + \(\frac{0.055}{12}\))1 + 100
b. Use the formula for the sum of a geometric series to calculate how much she will have in the bank after five years if she keeps on investing $100 per month.
Answer:
\(100\left(\frac{1-\left(1+\frac{0.055}{12}\right)^{60}}{1-\left(1+\frac{0.055}{12}\right)}\right)\) ≈ 6888.08
She will have approximately $6,888.08 in her account.
Question 10.
Nina has just taken out a car loan for $12,000. She will pay an annual interest rate of 3% through a series of monthly payments for 60 months, which she pays at the end of each month. The amount of money she has left to pay on the loan at the end of the nu month can be modeled by the function
f(n) = 86248 – 74248(1.0025)n for 0 ≤ n ≤ 60.
At the same time as her first payment (at the end of the first month), Nina placed $100 into a separate investment account that earns 6% per year compounded monthly. She placed $100 into the account at the end of each month thereafter. The amount of money in her savings account at the end of the nth month can be modeled by the function g(n) = 20000(1.005)n – 20000 for n ≥ 0.
a. Use the functions f and g to write an equation whose solution could be used to determine when Nina will have saved enough money to pay off the remaining balance on her car loan.
Answer:
86248 – 74248(1.0025)n = 20000(1.005)n – 20000
b. Use a calculator or computer to graph f and g on the same coordinate plane. Sketch the graphs below, labeling intercepts and indicating end behavior on the sketch. Include the coordinates of any intersection points.
Answer:
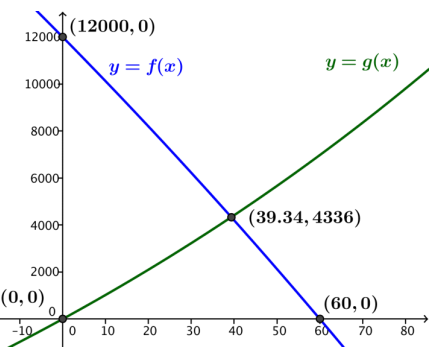
c. How would you interpret the end behavior of each function in the context of this situation?
Answer:
For g, the end behavior as x → ∞ indicates that the amount in the account will continue to grow over time at an exponential rate. For f, the end behavior as x → ∞ is not meaningful in this situation since the loan will be paid off after 60 months.
d. What does the intersection point mean in the context of this situation? Explain how you know.
Answer:
The intersection point indicates the time when the amount left on Nina’s loan is approximately equal to the amount she has saved. It is only approximate because the actual amounts are compounded/paid/deposited at the end of the month.
e. After how many months will Nina have enough money saved to pay off her car loan? Explain how you know.
Answer:
After 39.34 months, or at the end of the 40th month, she will have enough money saved to pay off the loan completely. The amount in her savings account at the end of the 40th month will be slightly more than $4,336, and the amount she has left on her loan will be slightly less than $4,336.
Question 11.
Each function below models the growth of three different trees of different ages over a fixed time interval.
Tree A:
f(t) = 15(1.69)\(\frac{t}{2}\), where t is time in years since the tree was 15 feet tall, f(t) is the height of the tree in feet, and 0 ≤ t ≤ 4.
Tree B:
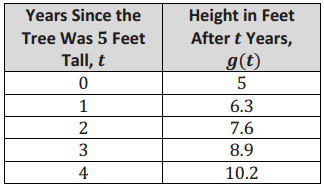
Tree C:
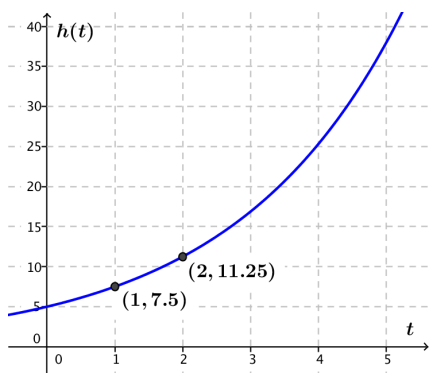
The graph of h is shown where t is years since the tree was 5 feet tall, and h(t) is the height in feet after t𝐠years.
a. Classify each function f, g, and h as linear or nonlinear. Justify your answers.
Answer:
The function f is exponential because it is of the form f(t) = abct, so f is nonlinear. The table for function appears to represent a linear function because its first differences are constant. The function h is nonlinear and appears to be an exponential function with common ratio 1.5.
b. Use the properties of exponents to show that Tree A has a percent rate of change of growth of 30% per year.
Answer:
The percent rate of change for f is 30% because (1.69)\(\frac{t}{2}\) = ((1.69)\(\frac{1}{2}\))t = (1.3)t = (1 + 0.3)t
c. Which tree, A or C, has the greatest percent rate of change of growth? Justify your answer.
Answer:
The percent rate of change for f is 30% by part (b). The percent rate of change for h is 50% because the common ratio is \(\frac{7.5}{5}=\frac{11.25}{7.5}\) = 1.5. Tree C has the greatest percent rate of change of growth.
d. Which function has the greatest average rate of change over the interval [0,4], and what does that mean in terms of tree heights?
Answer:
The average rate of change of f on [0,4] is \(\frac{15(1.69)^{\frac{4}{2}}-15}{4}\) ≈ 7. The average rate of change of g on the interval [0,4] is \(\frac{10.2-5}{4}\) = 1.3. The average rate of change of h, estimating from the graph, is approximately \(\frac{25.5-5}{4}\) = 5.125. The function with the greatest average rate of change is f, which means that over that four-year period, Tree A grew more feet per year on average than the other two trees.
e. Write formulas for functions g and h, and use them to confirm your answer to part(c).
Answer:
The functions are given by g(t) = 5 + 1.3t and h(t) = 5(\(\frac{3}{2}\))t. The average rate of change for g can be computed as \(\frac{g(4)-g(0)}{4}=\frac{10.2-5}{4}\) = 1.3, and the average rate of change for h on the interval [0,4] is \(\frac{h(4)-h(0)}{4}=\frac{25.3125-5}{4}\) = 5.078125.
f. For the exponential models, if the average rate of change of one function over the interval [0,4] is greater than the average rate of change of another function on the same interval, is the percent rate of change also greater? Why or why not?
Answer:
No. The average rate of change of f is greater than that of h over the interval of [0,4], but the percent rate of change of h is greater. The average rate of change is the rate of change over a specific interval, which varies with the interval chosen. The percent rate of change of an exponential function is the percent increase or decrease between the value of the function at x and the value of the function at x + 1 for any real number x; the percent rate of change is constant for an exponential function.
Question 12.
Identify which functions are exponential. For the functions that are exponential, use the properties of exponents to identify the percent rate of change, and classify the functions as indicating exponential growth or decay.
a. f(x) = 3(1 – 0.4)-x
Answer:
Since(1 – 0.4)-x = ((0.6)-1)x = \(\left(\left(\frac{6}{10}\right)^{-1}\right)^{x}=\left(\frac{10}{6}\right)^{x}\) ≈ (1.667)x, the percent rate of change for f is approximately 67%, which indicates exponential growth.
b. g(x) = \(\frac{3}{4^{x}}\)
Answer:
Since \(\frac{3}{4^{x}}\) = 3(\(\frac{1}{4}\))x = 3(0.25)x = 3(1 – 0.75)x, the percent rate of change for g is -75%, which indicates exponential decay.
c. k(x) = 3x0.4
Answer:
Since 3x0.4 = 3x\(\frac{4}{10}\) = \(3 \sqrt[10]{x^{4}}\) this is not a exponential function.
d. h(x) = 3\(\frac{x}{4}\)
Answer:
Since 3\(\frac{x}{4}\) = (3\(\frac{1}{4}\))x ≈ 1.316x, the percent growth is approximately 31.6%, which indicates exponenmtial growth.
Question 13.
A patient in a hospital needs to maintain a certain amount of a medication in her bloodstream to fight an infection. Suppose the initial dosage is 10 mg, and the patient is given an additional maintenance dose of 4 mg every hour. Assume that the amount of medication in the bloodstream is reduced by 25% every hour.
a. Write a function for the amount of the initial dosage that remains in the bloodstream after n hours.
Answer:
b(t) = 10(0.75)n
b. Complete the table below to track the amount of medication from the maintenance dose in the patient’s bloodstream for the first five hours.
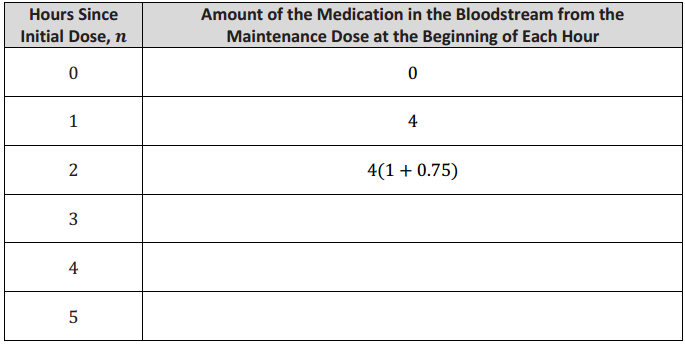
Answer:
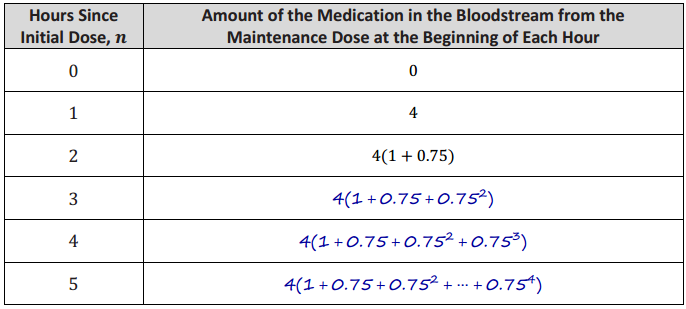
c. Write a function that models the total amount of medication in the bloodstream after n hours.
Answer:
d(n) = 10(0.75)n + 4\(\left(\frac{1-0.75^{n}}{1-0.75}\right)\)
d. Use a calculator to graph the function you wrote in part (c). According to the graph, will there ever be more than 16 mg of the medication present in the patient’s bloodstream after each dose is administered?
Answer:
According to the graph of the function in part (c), the amount of the medication approaches 16 mg as n→∞.
e. Rewrite this function as the difference of two functions (one a constant function and the other an exponential function), and use that difference to justify why the amount of medication in the patient’s bloodstream will not exceed 16 mg after each dose is administered.
Answer:
Rewriting this function gives d(n) = 16 – 6(0.75)n. Thus, the function is the difference between a constant function and an exponential function that is approaching a value of 0 as n increases. The amount of the medication will always be 16 reduced by an ever-decreasing quantity.